Comparing Quantities

8.1 Recalling Ratios and Percentages

· We know, ratio means comparing two quantities. A basket has two types of fruits, say, 20 apples and 5 oranges.

· Then, the ratio of the number of oranges to the number of apples = 5: 20.

· The comparison can be done by using fractions as, 5/ 20 = 1/ 4

· The number of oranges is 1/ 4th the number of apples. In terms of ratio, this is 1 : 4, read as, “1 is to 4”

· Number of apples to number of oranges = 20/ 4 = 5/ 1 = which means, the number of apples is 4 times the number of oranges.

· This comparison can also be done using percentages

Since contains it only apples and oranges,

So, percentage of apples + percentage of oranges = 100 or

Percentage of apples + 20 = 100 or

Percentage of apples = 100 – 20 = 80

Thus the basket has 20% oranges and 80% apples

There are 5 oranges out of 25 fruits.

So percentage of oranges is [Denominator made 100].

OR

By unitary method:

Out of 25 fruits, number of oranges are 5.

So out of 100 fruits, number of oranges = 5/25 100 = 20.

Example 1:

A picnic is being planned in a school for Class VII. Girls are 60% of the total number of students and are 18 in number.

The picnic site is 55 km from the school and the transport company is charging at the rate of Rs. 12 per km. The total cost of refreshments will be Rs. 4280.

Can you tell?

1. The ratio of the number of girls to the number of boys in the class?

2. The cost per head if two teachers are also going with the class?

3. If their first stop is at a place 22 km from the school, what per cent of the total distance of 55 km is this? What per cent of the distance is left to be covered?

Solution:

1. To find the ratio of girls to boys. Ashima and John came up with the following answers. They needed to know the number of boys and also the total number of students.

Ashima did this

Let the total number of students be x. 60% of x is girls.

Therefore, 60% of x = 18

60/ 100 × x = 18

Or

x = 18 100 / 60 = 30

Number of students = 30.

OR

John used the unitary method

There are 60 girls out of 100 students.

There is one girl out of 100 /60 students.

So, 18 girls are out of how many students?

Number of students = 100/60 ×18=30

So, the number of boys = 30 – 18 = 12.

Hence, ratio of the number of girls to the number of boys is 18: 12 or 18 /12 = 3/ 2.

3 /2 is written as 3: 2 and read as 3 is to 2.

2. To find the cost per person.

Transportation charge = Distance both ways × Rate

= Rs. (55 × 2) × 12 = Rs. 110 × 12 = Rs. 1320

Total expenses = Refreshment charge + Transportation charge

= Rs. 4280 + Rs. 1320 = Rs. 5600

Total number of persons =18 girls + 12 boys + 2 teachers

= 32 persons

Ashima and John then used unitary method to find the cost per head.

For 32 persons, amount spent would be Rs. 5600.

The amount spent for 1 person = Rs. 5600 /32 = Rs. 175.

3. The distance of the place where first stop was made = 22 km.

To find the percentage of distance:

Ashima used this method:

She is multiplying the ratio by =100/100=1and converting to percentage.

OR

John used the unitary method:

Out of 55 km, 22 km are travelled.

Out of 1 km, 22 55 km are travelled.

Out of 100 km, 22 55 × 100 km are travelled.

That is 40% of the total distance is travelled.

Both came out with the same answer that the distance from their school of the place where they stopped at was 40% of the total distance they had to travel.

Therefore, the percent distance left to be travelled = 100% – 40% = 60%.

8.2 Finding the Increase or Decrease Percent

We often come across such information in our daily life as.

(i) 25% off on marked prices

(ii) 10% hike in the price of petrol

Let us consider a few such examples.

Example 2: The price of a scooter was Rs. 34,000 last year. It has increased by 20% this year What is the price now?

Solution:

Amita said that she would first find the increase in the price, which is 20% of Rs. 34,000, and then find the new price.

20% of Rs. 34000 = Rs. 20/100 34000 = Rs. 6800

New price = Old price + Increase = Rs. 34,000 + Rs. 6,800 = Rs. 40,800

OR

Sunita used the unitary method. 20% increase means, Rs. 100 increased to Rs. 120.

So, Rs. 34,000 will increase to?

Increased price = Rs. 120 34000 100 × = Rs. 40,800

Similarly, a percentage decrease in price would imply finding the actual decrease followed by its subtraction the from original price.

Suppose in order to increase its sale, the price of scooter was decreased by 5%.

Then let us find the price of scooter.

Price of scooter = Rs. 34000

Reduction = 5% of Rs. 34000

= Rs. 5/100 34000 = Rs. 1700

New price = Old price – Reduction

= Rs. 34000 – Rs. 1700 = Rs. 32300

8.3 Finding Discounts

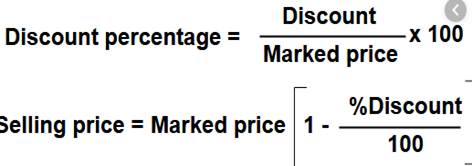
Discount is a reduction given on the Marked Price (MP) of the article. This is generally given to attract customers to buy goods or to promote sales of the goods. You can find the discount by subtracting its sale price from its marked price.

So, Discount = Marked price – Sale price

Example 3: An item marked at Rs. 840 is sold for Rs. 714. What is the discount and discount %?

Solution:

Discount = Marked Price – Sale Price = Rs. 840 – Rs. 714 = Rs. 126

Since discount is on marked price, we will have to use marked price as the base.

On marked price of Rs. 840, the discount is Rs. 126.

On MP of Rs. 100, how much will the discount be?

Discount = 126/840= 15%

You can also find discount when discount % is given.

Example 4: The list price of a frock is Rs. 220. A discount of 20% is announced on sales. What is the amount of discount on it and its sale price?

Solution:

Marked price is same as the list price. 20% discount means that on Rs. 100 (MP), the discount is Rs. 20.

By unitary method, on Rs.1 the discount will be Rs. 20/100.

On Rs. 220, discount = Rs. 20/100× 220 = Rs. 44

The sale price = (Rs. 220 – Rs. 44) or Rs. 176

Rehana found the sale price like this —

A discount of 20% means for a MP of Rs. 100, discount is Rs. 20.

Hence the sale price is Rs. 80.

Using unitary method, when MP is Rs. 100, sale price is Rs. 80;

When MP is Rs. 1, sale price is Rs. 80 / 100.

Hence when MP is Rs. 220, sale price = Rs. 80/100 × 220 = Rs. 176.

8.3.1 Estimation in percentages

Your bill in a shop is Rs. 577.80 and the shopkeeper gives a discount of 15%. How would you estimate the amount to be paid?

(i) Round off the bill to the nearest tens of Rs. 577.80, i.e., to Rs. 580.

(ii) Find 10% of this, i.e., .

(iii) Take half of this, i.e.,

(iv) Add the amounts in (ii) and (iii) to get Rs. 87.

You could therefore reduce your bill amount by Rs. 87 or by about Rs. 85, which will be Rs. 495 approximately.

1. Try estimating 20% of the same bill amount.

2. Try finding 15% of Rs. 375.

8.4 Prices Related to Buying and Selling (Profit and Loss)

Sometimes when an article is bought, some additional expenses are made while buying or before selling it. These expenses have to be included in the cost price.

These expenses are sometimes referred to as overhead charges.

These may include expenses like amount spent on repairs, labour charges, transportation etc.

8.4.1 Finding cost price/selling price, profit %/loss%

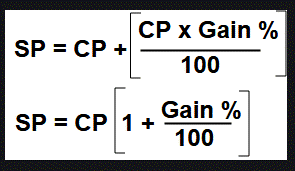
Example 5:

Sohan bought a second hand refrigerator for Rs. 2,500, then spent Rs. 500 on its repairs and sold it for Rs. 3,300. Find his loss or gain per cent.

Solution:

Cost Price (CP) = Rs. 2500 + Rs. 500 (overhead expenses are added to give CP)

= Rs. 3000

Sale Price (SP) = Rs. 3300

As SP > CP, he made a profit = Rs. 3300 – Rs. 3000 = Rs. 300

His profit on Rs. 3,000, is Rs. 300.

How much would be his profit on Rs. 100?

Profit

P% = P/CP

Example 6: A shopkeeper purchased 200 bulbs for Rs. 10 each. However 5 bulbs were fused and had to be thrown away. The remaining were sold at Rs. 12 each. Find the gain or loss %.

Solution:

Cost price of 200 bulbs = Rs. 200 × 10 = Rs. 2000

5 bulbs were fused.

Hence, number of bulbs left = 200 – 5 = 195

These were sold at Rs. 12 each.

The SP of 195 bulbs = Rs. 195 × 12 = Rs. 2340

He obviously made a profit (as SP > CP).

Profit = Rs. 2340 – Rs. 2000 = Rs. 340

On Rs. 2000, the profit is Rs. 340.

How much profit is made on Rs. 100? Profit = 340/2000 × 100% = 17%.

Example 7: Meenu bought two fans for Rs. 1200 each. She sold one at a loss of 5% and the other at a profit of 10%. Find the selling price of each. Also find out the total profit or loss.

Solution:

Overall CP of each fan = Rs. 1200. One is sold at a loss of 5%.

This means if CP is Rs. 100, SP is Rs. 95.

Therefore, when CP is Rs. 1200, then SP = Rs. 95/100× 120 = Rs. 1140

Also second fan is sold at a profit of 10%.

It means, if CP is Rs. 100, SP is Rs. 110.

Therefore, when CP is Rs. 1200, then SP = Rs. 110/100 ×1200 = Rs. 1320

Was there an overall loss or gain?

We need to find the combined CP and SP to say whether there was an overall profit or loss.

Total CP = Rs. 1200 + Rs. 1200 = Rs. 2400

Total SP = Rs. 1140 + Rs. 1320 = Rs. 2460

Since total SP > total CP, a profit of Rs. (2460 – 2400) or Rs. 60 has been made.

8.5 Sales Tax/Value Added Tax/Goods and Services Tax

The teacher showed the class a bill in which the following heads were written.

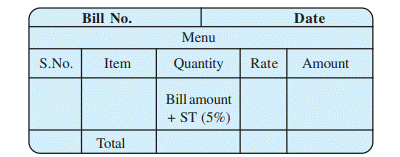
Sales tax (ST) is charged by the government on the sale of an item. It is collected by the shopkeeper from the customer and given to the government. This is, therefore, always on the selling price of an item and is added to the value of the bill. There is another type of tax which is included in the prices known as Value Added Tax (VAT).

From July 1, 2017, Government of India introduced GST which stands for Goods and Services Tax which is levied on supply of goods or services or both.

Example 8: (Finding Sales Tax) the cost of a pair of roller skates at a shop was Rs. 450. The sales tax charged was 5%. Find the bill amount.

Solution:

On Rs. 100, the tax paid was Rs. 5.

On Rs. 450, the tax paid would be = 5/100= Rs. 22.50

Bill amount = Cost of item + Sales tax = Rs. 450 + Rs. 22.50 = Rs. 472.50.

Example 9: (Value Added Tax (VAT)) Waheeda bought an air cooler for Rs. 3300 including a tax of 10%. Find the price of the air cooler before VAT was added.

Solution:

The price includes the VAT, i.e., the value added tax.

Thus, a 10% VAT means if the price without VAT is Rs. 100 then price including VAT is Rs. 110. Now, when price including VAT is Rs. 110, original price is Rs. 100.

Hence when price including tax is Rs. 3300,

The original price = Rs. 100/110 3300 = 3000.

Example 10: Salim bought an article for Rs. 784 which included GST of 12%. What is the price of the article before GST was added?

Solution:

Let original price of the article be Rs. 100.

GST = 12%. Price after GST is included = Rs. (100+12) = Rs. 112

When the selling price is Rs. 112 then original price = Rs. 100.

When the selling price is Rs. 784, then original price = Rs. 100/12 784 = Rs. 700

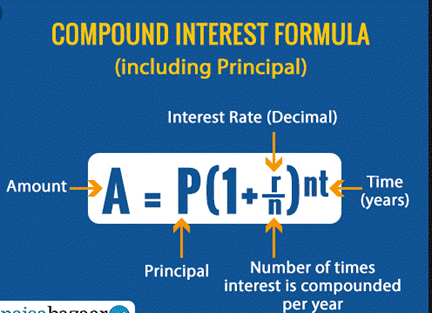
8.6 Compound Interest

You might have come across statements like “one year interest for FD (fixed deposit) in the bank @ 9% per annum” or ‘Savings account with interest @ 5% per annum’.

· Interest is the extra money paid by institutions like banks or post offices on money deposited (kept) with them. Interest is also paid by people when they borrow money. We already know how to calculate Simple Interest

Example 10: A sum of Rs. 10,000 is borrowed at a rate of interest 15% per annum for 2 years. Find the simple interest on this sum and the amount to be paid at the end of 2 years.

Solution:

On Rs. 100, interest charged for 1 year is Rs. 15.

So, on Rs. 10,000, interest charged = 15/100 = Rs. 1500

Interest for 2 years = Rs. 1500 × 2 = Rs. 3000

Amount to be paid at the end of 2 years

= Principal + Interest

= Rs. 10000 + Rs. 3000 = Rs. 13000

· My father has kept some money in the post office for 3 years. Every year the money increases as more than the previous year.

· We have some money in the bank. Every year some interest is added to it, which is shown in the passbook. This interest is not the same, each year it increases.

· Normally, the interest paid or charged is never simple. The interest is calculated on the amount of the previous year. This is known as interest compounded or Compound Interest (C.I.).

Calculating Compound Interest

A sum of Rs. 20,000 is borrowed by Heena for 2 years at an interest of 8% compounded annually. Find the Compound Interest (C.I.) and the amount she has to pay at the end of 2 years.

Aslam asked the teacher whether this means that they should find the interest year by year. The teacher said ‘yes’, and asked him to use the following steps:

1. Find the Simple Interest (S.I.) for one year.

Let the principal for the first year be P. Here, P = Rs. 20,000

SI = SI at 8% p.a. for 1st year = Rs. 20000/100 ×8 = Rs. 1600

2. Then find the amount which will be paid or received. This becomes principal for the next year.

Amount at the end of 1st year = P + SI = Rs. 20000 + Rs. 1600

= Rs. 21600 = P (Principal for 2nd year)

3. Again find the interest on this sum for another year.

SI= SI at 8% p.a.for 2nd year = Rs. 21600/100 ×8

= Rs. 1728

4. Find the amount which has to be paid or received at the end of second year.

Amount at the end of 2nd year = P+ SI = Rs. 21600 + Rs. 1728 = Rs. 23328

Total interest given = Rs. 1600 + Rs. 1728 = Rs. 3328

Reeta asked whether the amount would be different for simple interest.

The teacher told her to find the interest for two years and see for herself.

SI for 2 years = Rs. 20000 8 2 / 100 = Rs. 3200

Reeta said that when compound interest was used Heena would pay Rs. 128 more. Let us look at the difference between simple interest and compound interest. We start with Rs. 100. Try completing the chart.

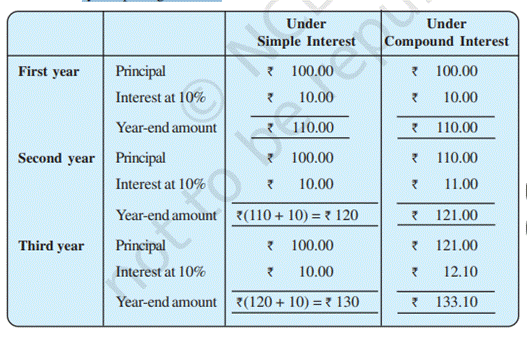
Note that in 3 years,

Interest earned by Simple Interest = Rs. (130 – 100) = Rs. 30, whereas,

Interest earned by Compound Interest = Rs. (133.10 – 100) = Rs. 33.10

Note also that the Principal remains the same under Simple Interest, while it changes year after year under compound interest.

8.7 Deducing a Formula for Compound Interest

Suppose P1 is the sum on which interest is compounded annually at a rate of R% per annum. Let P1 = Rs. 5000 and R = 5. Then by the steps mentioned above

1. SI1=

So, A1 = Rs. 5000 +

= Rs. 5000 (1+ 5/100) = P2 OR

SI1= P1R11 / 100

A1 = P1 + SI1 = P1 + P1R/100

= P1 (1+ R1/100) = P2

2. SI2 = Rs. 5000(1+ 5/ 100) 51/100 OR SI2 = P2 R1/ 100

= Rs. 5000 5/ 100 (1+5/ 100) =P1 (1+ R/100) R/100

= P1 R/100 (1+R/100)

A2 = Rs. A2 = P2 + SI2

=P1 (1+R/100) +P1R/100(1+R/100)

= P3 =P1 (1+R/100) + (1+R/100)

=P1 (1+R/100) = P3

Proceeding in this way the amount at the end of n years will be

A = P1 (1+R/100),

We can say A = P1 (1+R/100)

Aruna at once said that we know CI = A – P, so we can easily find the compound interest too.

Example 11: Find CI on Rs. 12600 for 2 years at 10% per annum compounded annually.

Solution:

We have, A = P1 (1+R/100) ,

Where Principal (P) = Rs. 12600, Rate (R) = 10, Number of years (n) = 2

= Rs. 12600 (1+ 10/100)

= Rs. 12600 (11 /10)

= Rs. 12600 = Rs. 15246

CI = A – P = Rs. 15246 – Rs. 12600 = Rs. 2646

8.8 Rate Compounded Annually or Half Yearly (Semi Annually)

· Time period and rate when interest not compounded annually the time period after which the interest is added each time to form a new principal is called the conversion period. When the interest is compounded half yearly, there are two conversion periods in a year each after 6 months.

· In such situations, the half yearly rate will be half of the annual rate. What will happen if interest is compounded quarterly? In this case, there are 4 conversion periods in a year and the quarterly rate will be one-fourth of the annual rate.

Example 13: Find CI paid when a sum of Rs. 10,000 is invested for 1 year and 3 months at 8 ½ % per annum compounded annually.

Solution:

Mayuri first converted the time in years.

1 year 3 months = 1 3/12 year = 1 1/4 years

Mayuri tried putting the values in the known formula and came up with:

A =

Now she was stuck. She asked her teacher how she would find a power which is fractional. The teacher then gave her a hint:

Find the amount for the whole part, i.e., 1 year in this case.

Then use this as principal to get simple interest for 1/4 year more.

Thus,

A = Rs. 10000(1 +17 /200) +

= Rs. 10000 × 217/ 200 = Rs. 10,850

Now this would act as principal for the next 1/ 4 year.

We find the SI on Rs. 10,850 for 1/4 year.

SI =10850 /

= 1085017 /800

= Rs. 230.56

Interest for first year = Rs. 10850 – Rs. 10000 = Rs. 850 and, interest for the next 1/4 year

= Rs. 230.56 Therefore, total compound Interest = 850 + 230.56 = Rs. 1080.56.

8.9 Applications of Compound Interest Formula

There are some situations where we could use the formula for calculation of amount in CI. Here are a few.

(i) Increase (or decrease) in population.

(ii) The growth of a bacteria if the rate of growth is known.

(iii) The value of an item, if its price increases or decreases in the intermediate years.

Example 14: The population of a city was 20,000 in the year 1997. It increased at the rate of 5% p.a. Find the population at the end of the year 2000.

Solution:

There is 5% increase in population every year, so every New Year has new population. Thus, we can say it is increasing in compounded form.

Population in the beginning of 1998 = 20000

Increase at 5% = 5/100 =1000

= Population in 1999 = 20000 + 1000 = 21000

Increase at 5% =

= Population in 2000 = 21000 + 1050 = 22050

Increase at 5% = = 1102.5

At the end of 2000 the population = 22050 + 1102.5 = 23152.5

Or,

Population at the end of 2000 =

=

So, the estimated population = 23153.

Example 15: A TV was bought at a price of Rs. 21,000. After one year the value of the TV was depreciated by 5% (Depreciation means reduction of value due to use and age of the item). Find the value of the TV after one year.

Solution:

Principal = Rs. 21,000 Reduction = 5% of Rs. 21000 per year

= Rs. 21000 1/ 100 = Rs. 1050

Value at the end of 1 year = Rs. 21000 – Rs. 1050 = Rs. 19,950

Alternately,

We may directly get this as follows:

Value at the end of 1 year = Rs. 21000(1- 5/ 100) = Rs. 21000 × 19/ 20 = 19,950