Mensuration
It is all about the measurement
of area, perimeter and volume of the plane and solid figures.

Area
·
The surface covered by the border line of the
figure is the area of the plain shape.
·
Unit of the area is square if the length unit.
Perimeter
·
The perimeter is the length of the boundary of the
plane shape.
·
The unit of the perimeter is same as the length unit.
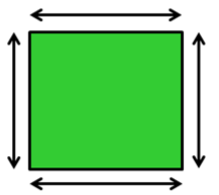
The
green part is the area of the square and the distance all the way around the
outside is the perimeter.
Area and Perimeter of Some 2D Shapes
|
Shape |
Image |
Area |
Perimeter |
|
Square |
|
(Side)2 |
4 × Side |
|
Rectangle |
|
Length ×
Breadth |
2(Length +
Breadth) |
|
Triangle |
|
(1/2) ×
Base × Height |
a + b + c |
|
Parallelogram |
|
Base ×
Height |
2(sum of
adjacent sides) |
|
Circle |
|
πr2 |
2πr |
Area of Trapezium
A trapezium is a quadrilateral
whose two sides are parallel. And if its non-parallel sides are equal then it
is said to be an isosceles trapezium.
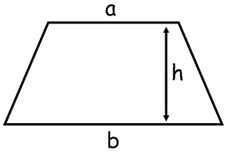
Area of Trapezium can be found,
1. By Splitting the figure
One
way to find the Area of trapezium is to divide it into two or three plane
figures and then find the area.
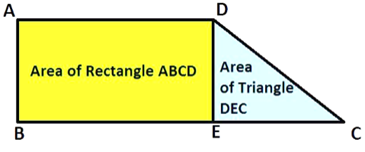
In the
trapezium ABCD,
It can
be divided into two parts i.e. a rectangle and a triangle.
Area
of ABCD = Area of ABED + Area of DEC
2. By using formula
Another
way is to calculate the area by using formula.
![]()
Area
of trapezium is half of the product of the summation of the parallel sides and
the perpendicular distance between them.
Example
Find
the area of the trapezium whose parallel sides are 6 cm and 16 cm, with a
height of 5 cm. Calculate the area using both the
methods.
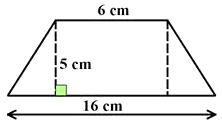
Solution:
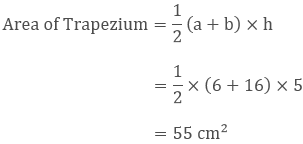
Splitting
the trapezium we get –
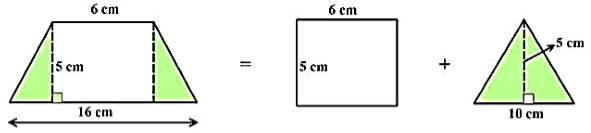
Area
of the trapezium = Area of rectangle + Area of a triangle
= (6 x
5) + (1/2) x 5 x 10
= 30 +
25
= 55
cm2
Remark: We should use the
formula most of the time if possible as it is the quick and easy method.
Area of a General Quadrilateral
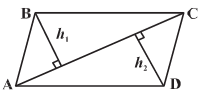
To
find the area of any quadrilateral we can divide it into two triangles and then
the area can be easily calculated by calculating the area of both the triangles
separately.
Area
of ABCD = Area of ∆ABC + Area of ∆ACD
= (1/2) × AC × h1 +
(1/2) × AC× h2
The formula for the Area of a General Quadrilateral
![]()
Where
h1 and h2 are the height of both the triangles
and d is the length of common diagonal i.e.AC.
Example
Find
the area of quadrilateral ABCD.
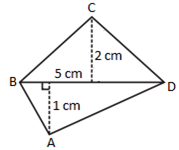
Solution:
In the
quadrilateral ABCD,
BD is
the common diagonal so d = 5 cm.
Height
of the two triangles are h1 = 2 cm and h2 = 1
cm.
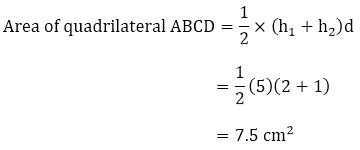
Area of Special Quadrilaterals (Rhombus)
A rhombus is a quadrilateral with
all the sides are equal and parallel but not the right angle. Its two diagonals
are the perpendicular bisector to each other.
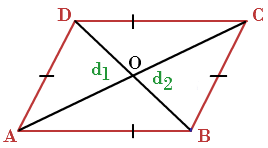
In
this also we can split the rhombus into two triangles and can find the area of
rhombus easily.
Formula of Area of Rhombus
![]()
Area
of rhombus is half of the product of its two diagonals.
Area of a Polygon
There is no particular formula
for the area of the polygon so we need to divide it in a possible number of
figures like a triangle, rectangle, trapezium and so
on. By adding the area of all the split figures we will get the area of the
required polygon.
Example
Find
the area of the given octagon.
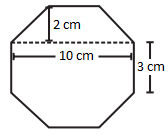
Solution:
We can divide the given octagon
into three parts.
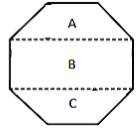
Two
trapezium A and B and one rectangle shown by part B.
Two
trapezium A and B and one rectangle shown by part B.
Area
of A = Area of B = (1/2) × (a + b) × h
=
(1/2) x (10 + 3) × 2
=
13 cm2.
Area
of B = Length x Breadth
=
10 x 3
=
30 cm2.
So,
the area of Octagon = 2A + B
=
2 × 13 + 30
=
56 cm2.
Solid Shapes
The 3-dimensional shapes which
occupy some space are called solid shapes. Example- Cube, Cylinder, Sphere etc.
Surface Area
If we draw the net of the solid
shape then we can see it’s all the faces clearly and if we add the areas of all
the faces then we get the total surface area of that solid shape. The unit of
surface area is a square unit.
Lateral or Curved Surface Area
If we leave the top and bottom
faces of the solid shape then the area of the rest of the figure is the lateral
surface of the shape. The unit of lateral surface area is a square unit.
Surface Area of Cube, Cuboid and Cylinder
|
Name |
Figure |
Lateral or Curved Surface Area |
Total Surface Area |
Nomenclature |
|
Cube |
|
4l2 |
6l2 |
l = Edge of the cube |
|
Cuboid |
|
2h(l + b) |
2(lb + bh + lh) |
l = Length, b = Breadth, h = Height |
|
Cylinder |
|
2πrh |
2πr2+ 2πrh
= 2πr(r + h) |
r = Radius, h = Height |
Volume
Volume is the space occupied by
any solid figure i.e. the amount of capacity to carry something is the volume
of that solid shape. The unit of volume is a cubic unit.
Volume of Cube, Cuboid and Cylinder
|
Name |
Volume |
Nomenclature |
|
Cube |
l3 |
l = Edge
of the cube |
|
Cuboid |
lbh |
l =
Length, b = Breadth, h = Height |
|
Cylinder |
πr2h |
r =
Radius, h = Height |
Example
1
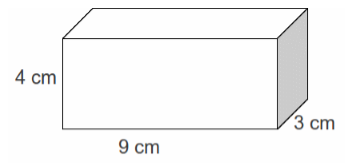
There
is a shoe box whose length, breadth and height is 9 cm, 3 cm and 4 cm
respectively. Find the surface area and volume of the shoe box.
Solution:
Given,
Length
= 9 cm
Breadth
= 3 cm
Height
= 4 cm
Area
of cuboid = 2(lb + bh + lh)
=
2(9 × 3 + 3×4 + 9 × 4)
=
2(27 + 12 + 36)
=
2(75)
=
150 cm2
Volume
of cuboid = lbh
=
9 × 3 × 4
=
108 cm3
Example
2
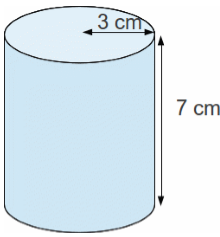
If
there is a cold drink can whose height is 7 cm and the radius of its round top
is 3 cm then what will be the lateral surface area and volume of that cylinder?
(π = 3.14)
Solution:
Given,
Radius
= 3 cm
Height
= 7 cm
Lateral
surface area of cylinder = 2πrh
=
2 × 3.14 × 3 × 7
=
131.88 cm2
Volume
of cylinder = πr2h
=
3.14 × 3 × 3 × 7
=
197.82 cm3
Example
3
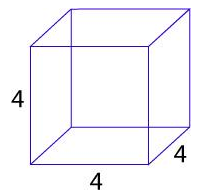
If
there is a box of cube shape with the length of 4 cm then what will be the
capacity of this box. Also, find the surface area of the box if it is open from
the top.
Solution:
Given,
side = 4 cm
Capacity
or volume of the box = s3
=
43 = 64 cm3
The
total surface area of the box = 6s2
But,
if the box is open from the top then the surface area will be total surface
area minus the area of one face of the cube.
Surface
Area = Total Surface Area - Area of one face
=
6s2 – s2
=
5s2 = 5 × 42
=
80 cm2
Volume and Capacity
·
Volume and capacity are one and the same thing.
·
Volume is the amount of space occupied by a shape.
·
Capacity is the quantity that a container can hold.
·
Capacity can be measured in form of liters.
We can
see the relation between liter and cm3 as,
1 L =
1000 mL
1 mL =
1 cm3,
1 L =
1000 cm3.
Thus,
1 m3 = 1000000 cm3 = 1000 L.






