Visualising Solid Shapes

There are three types of shapes:

One dimensional shapes

Shapes having length only. Example: a line.

Two-dimensional shapes

Plane figures with only two measurements –length and width are called 2-D shapes.

Three-dimensional shapes

Solid figures with three measurements –length, width and height are called 3D shapes.

Views of 3D-Shapes

As the 3-D shapes are solid in nature so they may have a different view from different sides.

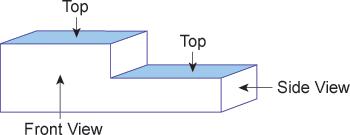
When we draw the top view, front view and side view on paper then it will look like this.

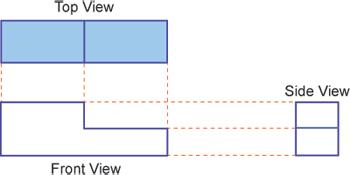
Example

Draw the front view, side view and the top view of the given figure.

Solution

Mapping Space around Us

A map shows the location of a particular thing with respect to others.

Some important points related to map:

· To represent different objects or place different symbols are used.

· A map represents everything proportional to their actual size not on the basis of perspective. It means that the size of the object will remain the same irrespective of the observer’s viewpoint.

· A particular scale is used to draw a map so that the lengths drawn are proportional with respect to the size of the original figures.

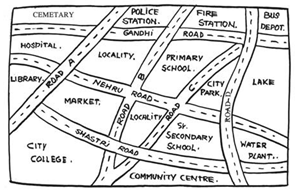
This is the map which shows the different routes from Nehru road.

Faces, Edges and Vertices

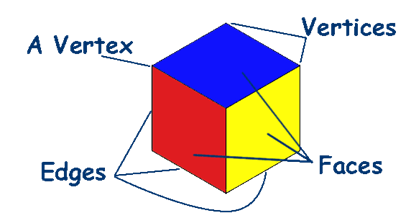
· Faces – All the flat surfaces of the three 3-D shapes are the faces. Solid shapes are made up of these plane figures called faces.

· Edges – The line segments which make the structure of the solid shapes are called edges. The two faces meet at the edges of the 3D shapes.

· Vertex – The corner of the solid shapes is called vertex. The two edges meet at the vertex. The plural of the vertex is vertices.

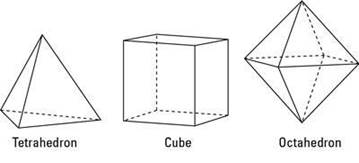
Polyhedrons

Polygons are the flat surface made up of line segments. The 3-D shapes made up of polygons are called polyhedron.

· These solid shapes have faces, edges and vertices.

· The polygons are the faces of the solid shape.

· Three or more edges meet at a point to form a vertex.

· The plural of word polyhedron is polyhedral.

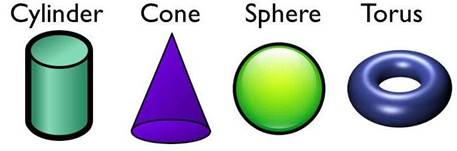
Non-polyhedron

The solid shape who’s all the faces are not polygon are called non-polyhedron. i.e. it has one of the curved faces.

Convex Polyhedrons

If the line segment formed by joining any two vertices of the polyhedron lies inside the figure then it is said to be a convex polyhedron.

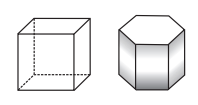
Non-convex or Concave Polyhedron

If anyone or more line segments formed by joining any two vertices of the polyhedron lie outside the figure then it is said to be a non-convex polyhedron.

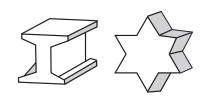
Regular Polyhedron

If all the faces of a polyhedron are regular polygons and its same number of faces meets at each vertex then it is called regular polyhedron.

Non-regular Polyhedron

The polyhedron which is not regular is called non-regular polyhedron. Its vertices are not made by the same number of faces.

In this figure, 4 faces meet at the top point and 3 faces meet at all the bottom points.

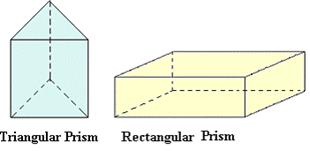
Prism

If the top and bottom of a polyhedron are a congruent polygon and its lateral faces are parallelogram in shape, then it is said to be a prism.

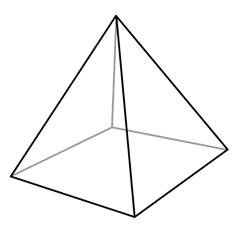
Pyramid

If the base of a polyhedron is the polygon and its lateral faces are triangular in shape with a common vertex, then it is said to be a pyramid.

Number of faces, vertices and edges of some polyhedrons

Solid	Number of Faces	Number of Edges	Number of Vertices
Cube	6	12	8
Rectangular Prism	6	12	8
Triangular Prism	5	9	6
Pentagonal Prism	7	15	10
Hexagonal Prism	8	18	12
Square Pyramid	5	8	5
Triangular Pyramid	4	6	6
Pentagonal Pyramid	6	10	6
Hexagonal Pyramid	7	12	7

Euler’s formula

· Euler’s formula shows the relationship between edges, faces and vertices of a polyhedron.

· Every polyhedron will satisfy the criterion F + V – E = 2,

· Where F is the number of faces of the polyhedron, V is the vertices of the polyhedron and E is the number of edges of the polyhedron.

Example

Using Euler's formula, find the number of faces if the number of vertices is 6 and the number of edges is 12.

Solution

Given, V = 6 and E = 12.

We know Euler’s formula, F + V – E = 2

So, F + 6 – 12 = 2.

Hence, F = 8.