CONSTRUCTION

Introduction:

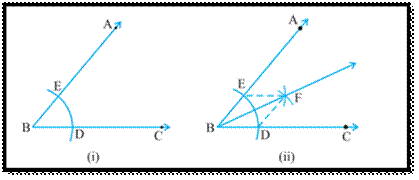
For constructing the angle bisector of angle ABC, take B as a centre construct an arc (any radius) intersecting the rays BA and BC at D and E. Now take E and D as centres and radius more than ½ DE, construct arcs such that they intersect with each other at F.

A line is a collection of points along a straight path which extends to both the directions without endpoints.

AB is a line which doesn’t have an ending.

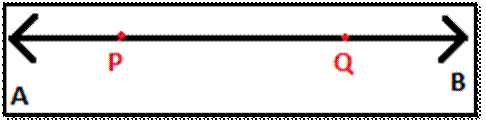
A line segment is a part of a line between two endpoints.

PQ is a line segment having P and Q as endpoints on the line AB.

Division of a line segment :

A line segment can be divided into ‘n’ equal parts, where ‘n’ is any natural number.

For example;

A Line Segment of length 10 cm is divided into two equal parts by using a ruler as,

Mark a point 5 cm away from one end.

10 cm is divided into two 5 cm line segments.

Similarly, a line segment of length 15 cm can be divided in the ratio 2:1 as,

AB is the line segment of length 15 cm and C divides the line in the ratio 2:1.

Let CB = x, then AC = 2x

AC + CB = 2x + x = 15, x = 5

AC = 10 cm and CB = 5 cm.

Mark point C, 10 cm away from A

Now, what if we cannot measure the lengths precisely? We will not be able to mark the point correctly.

There is a better way to mark point while dividing a line in a given ratio, which explained as follows.

Alternative Method:

Consider a line PQ←→ . We have to divide PQ←→ in a ratio m:n, where m and n are positive integers.

Let m = 3 and n = 1. So, we are dividing the line PQ←→ in the ratio 3 : 1.

Steps of construction :

Draw PQ←→ a ray PX which makes acute angle with PQ←→

Since the given ratio is 3:1, the number of points to be located on PX should be 4. Because(m + n = 3 + 1) . Now mark the points A, B, C and D such that PA = AB = BC = CD using compass. Draw an arc with a measure of n/4, from the centre P and name it as A. Drawing another arc by taking the centre as the first marked arc (A), draw an arc with the same measure and name it as B. Similarly, do it for other two arcs, also. (For example, if the measure of the line segment pQ = 20 cm, divide 20 by 4, we will get 5. Now, take the compass and measure 5 cm. Take P as a centre and draw an arc on PX and mark that point as A. Now take A as a centre and draw another arc on the same ray PX and mark it as B. Similarly, repeat this process for 2 more times and mark it as C and D).

Join Q and D using a ruler.

Draw a line through the point C (m = 3, C is the third point from P) which should be parallel to QD←→ by making an equal angle to ∠PDQ intersect the line PQ at R. (Refer figure.)

Now, R is the point on PQ←→ ⃡which divides PQ←→  in the ratio 3:1.

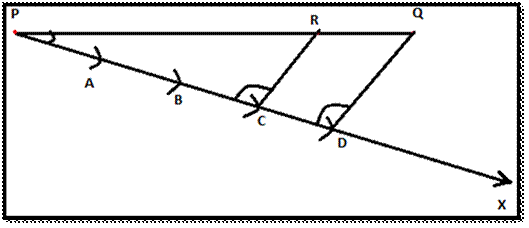
Figure 1

Division of a line segment

Since CR is parallel to DQ;

By basic proportionality theorem,

PRRQ = PCCD

By construction, PCCD  = 31

Therefore,

PRRQ  = 31

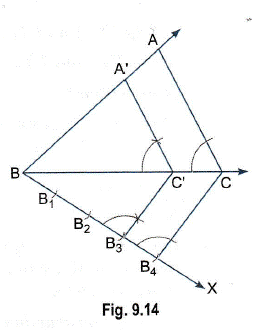
1. Construct a triangle similar to a given triangle ABC with its sides equal to 3/4 of the corresponding sides of the triangle  ABC(i.e., of scale factor 3/4).

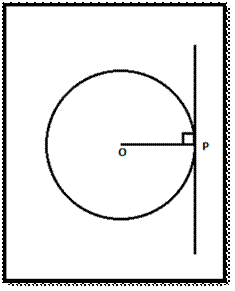
Construction of Tangents to a Circle :

Let’s see how to draw a tangent to a circle at a point on the circle. (Refer fig.)

Step 1: Draw a circle with the required radius with centre O

Step 2:  Join centre of the circle O and any point P on the circle. OP is the radius of the circle

Step 3: Draw a line perpendicular to radius OP through point P. This line will be a tangent to the circle at P

Two tangents can be drawn to a circle from a point outside of the circle. Lengths of the two tangents will be equal.

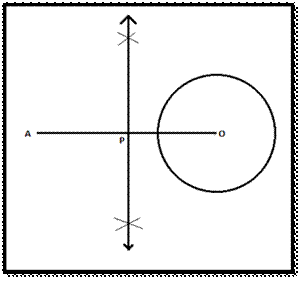
Construction of Two Tangents from a Point Outside of the Circle :

Step 1: Consider a point A from the outside the circle with centre O.

Step 2:  Join points A and O, bisect the line AO. Let P be the midpoint of AO.

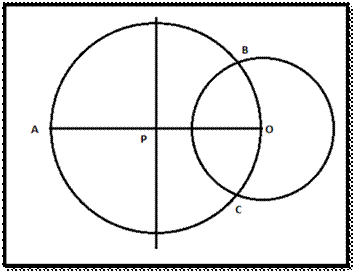
Step 3: Draw a circle taking P as centre and PO as a radius. This circle will intersect at two points B and C on the circle with centre O.

Step 4: Join the point A with B and C. AB and AC are the required tangents through points B and C on the circle.

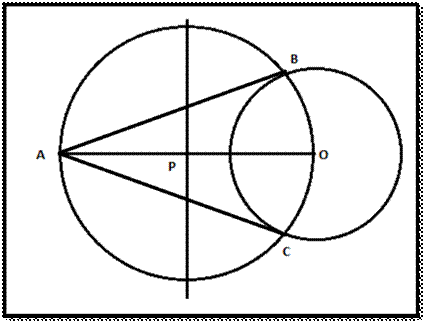
To construct the tangents to a circle from a point outside it.

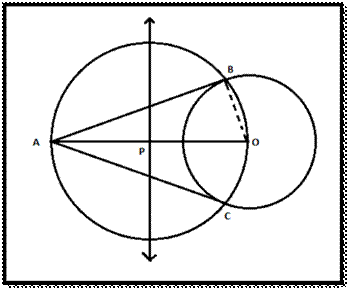
It is observed that AO is a diameter of the circle with centre P. By construction, ∠ABO is an angle in a semi-circle.

Therefore,

∠ABO = 90°

Since OB is the radius of the circle with centre O, AB has to the tangent through the point B.

Similarly, AC is the tangent through the point C.