Introduction Of Coordinate Geometry

A system of geometry where the position of points on the plane is described using an ordered Pair of numbers.

Recall that a plane is a flat surface that goes on forever in both directions. If we were to place a point on the plane, coordinate geometry gives us a way to describe exactly where it is by using two numbers.

What is coordinate geometry?

Grid with rows and columns labelled.

To introduce the idea, consider the grid above. The columns of the grid are lettered A,B,C etc. The rows are numbered 1,2,3etc from the top. We can see that the X is in box D3; that is, column D, row 3.

D and 3 are called the coordinates of the box.

It has two parts:

the row

the column.

There are many boxes in each row and many boxes in each column. But by having both we can find one single box, where the row and column intersect.

COORDINATE PLANE:

In coordinate geometry, points are placed on the "coordinate plane" as shown below. It has two scales - one running across the plane called the "x axis" and another a right angles to it called the y axis. (These can be thought of as similar to the column and row in the paragraph above.) The point where the axes cross is called the origin and is where both x and y are zero.

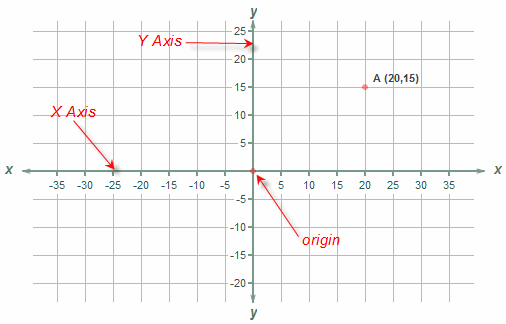
coordinate plane showing x-axis, y-axis and origin

Ø On the x-axis, values to the right are positive and those to the left are negative.
On the y-axis, values above the origin are positive and those below are negative.

A point's location on the plane is given by two numbers, the first tells where it is on the x-axis and the second which tells where it is on the y-axis. Together, they define a single, unique position on the plane. So in the diagram above, the point A has an x value of 20 and a y value of 15. These are the coordinates of the point A, sometimes referred to as its "rectangular coordinates".

Note :

That the order is important; the x coordinate is always the first one of the pair.

CARTESIAN COORDINATES:

Cartesian Coordinates:

Cartesian coordinates allow one to specify the location of a point in the plane, or in three-dimensional space. The Cartesian coordinates (also called rectangular coordinates) of a point are a pair of numbers (in two-dimensions) or a triplet of numbers (in three-dimensions) that specified signed distances from the coordinate axis.

Cartesian coordinates of the plane:

The Cartesian coordinates in the plane are specified in terms of the xx coordinates axis and the yy-coordinate axis, as illustrated in the below figure. The origin is the intersection of the xx and yy-axes.

The Cartesian coordinates of a point in the plane are written as (x,y)(x,y). The first number xx is called the xx-coordinate (or xx-component), as it is the signed distance from the origin in the direction along the xx-axis. The xx-coordinate specifies the distance to the right (if xx is positive) or to the left (if xx is negative) of the yy-axis.

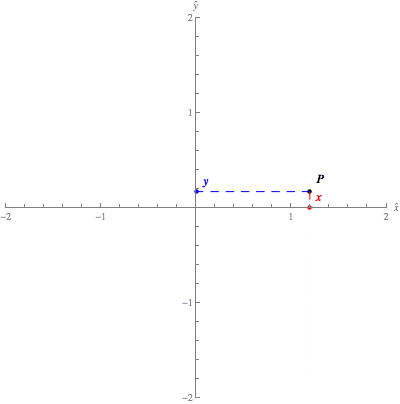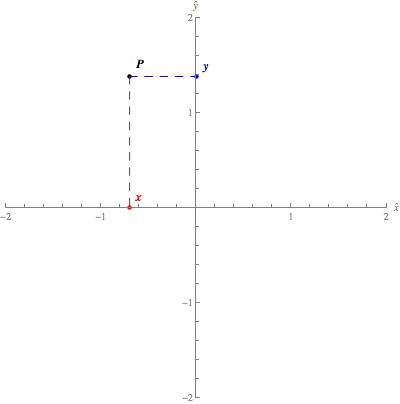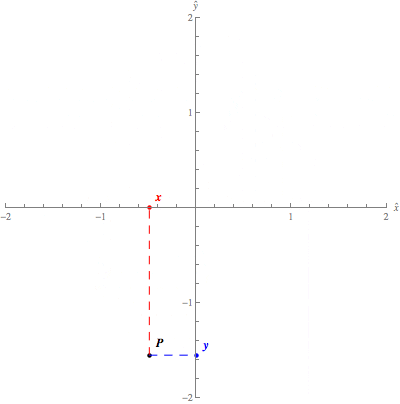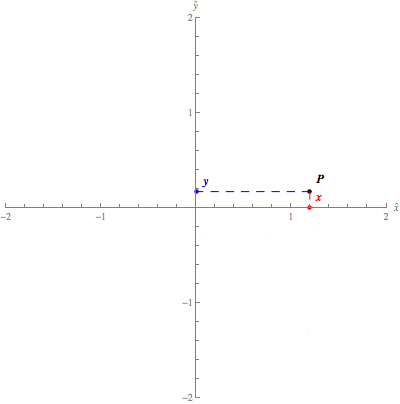
Similarly, the second number yy is called the yy-coordinate (or yy-component), as it is the signed distance from the origin in the direction along the yy-axis, The yy-coordinate specifies the distance above (if yy is positive) or below (if yy is negative) the xx-axis. The following figure, the point has coordinates (−3,2)(−3,2), as the point is three units to the left and two units up from the origin.

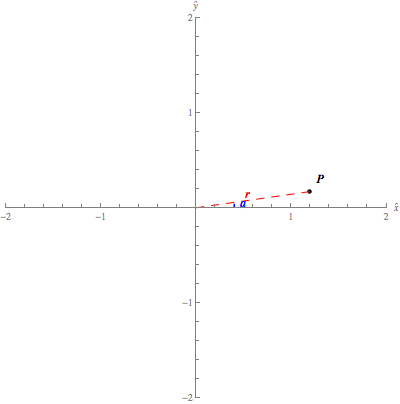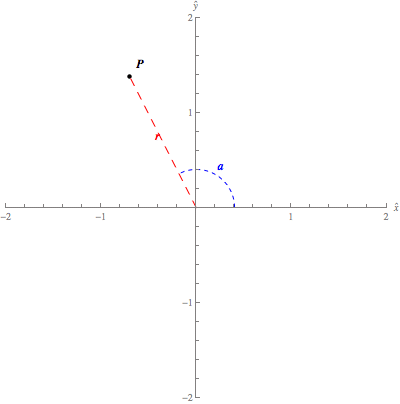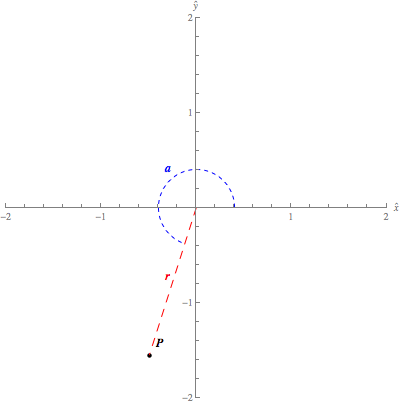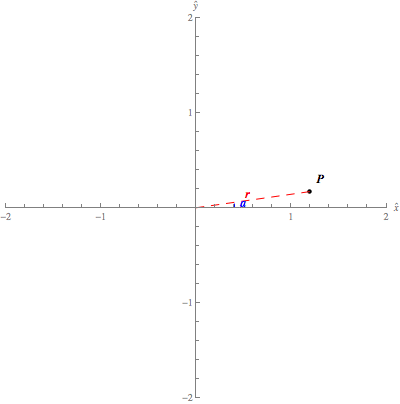
The below applet illustrates the Cartesian coordinates of a point in the plane. It's similar to the above figure, only it allows you to change the point.

Cartesian coordinates in the plane. The Cartesian coordinates (x,y)(x,y) of the blue point specify its location relative to the origin, which is the intersection of the xx- and yy-axis. You can change the location of the point by dragging it with your mouse.

Image result for Cartesian Systemgif

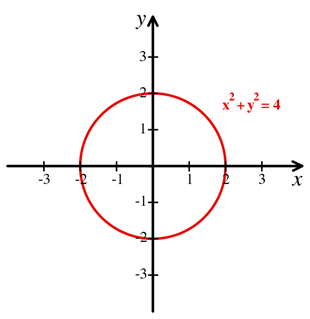
Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by algebraic equations, namely equations satisfied by the coordinates of the points lying on the shape. For example, a circle of radius 2 may be described by the equation x² + y² = 4 (see Figure 2).

TWO-DIMENSIONAL COORDINATE SYSTEM :

The four quadrants of a Cartesian coordinate system. The arrows on the axes indicate that they extend forever in their respective directions (i.e. infinitely).

A Cartesian coordinate system in two dimensions is commonly defined by two axes, at right angles to each other, forming a plane (an xy -plane). The horizontal axis is normally labelled x, and the vertical axis is normally labelled y.

In a three–dimensional coordinate system, another axis, normally labelled z, is added, providing a third dimension of space measurement. The axes are commonly defined as mutually orthogonal to each other (each at a right angle to the other).All the points in a Cartesian coordinate system taken together form a so-called Cartesian plane. Equations that use the Cartesian coordinate system are called Cartesian equations.

Image result for Two-dimensional coordinate system gif

The point of intersection, where the axes meet, is called the origin normally labeled O. The x and y axes define a plane that is referred to as the xy plane. Given each axis, choose a unit length, and mark off each unit along the axis, forming a grid. To specify a particular point on a two dimensional coordinate system, indicate the x unit first (abscissa), followed by the y unit (ordinate) in the form (x,y), an ordered pair.

The choice of letters comes from a convention, to use the latter part of the alphabet to indicate unknown values. In contrast, the first part of the alphabet was used to designate known values.

THREE-DIMENSIONAL COORDINATE SYSTEM :

Three dimensional Cartesian coordinate system with y-axis pointing away from the observer.

Three dimensional Cartesian coordinate system with the x-axis pointing towards the observer.

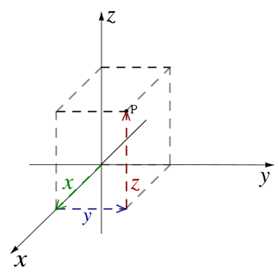
The three dimensional Cartesian coordinate system provides the three physical dimensions of space—length, width, and height .

The three Cartesian axes defining the system are perpendicular to each other. The relevant coordinates are of the form (x,y,z).

Image result for Two-dimensional coordinate system gif

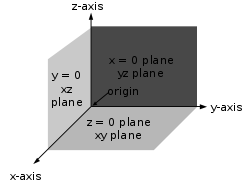
The xy-, yz-, and xz-planes divide the three-dimensional space into eight subdivisions known as octants, similar to the quadrants of 2D space.

In two dimensions

Fixing or choosing the x-axis determines the y-axis up to direction. Namely, the y-axis is necessarily the perpendicular to the x-axis through the point marked 0 on the x-axis. But there is a choice of which of the two half lines on the perpendicular to designate as positive and which as negative. Each of these two choices determines a different orientation (also called handedness) of the Cartesian plane.

The usual way of orienting the axes, with the positive x-axis pointing right and the positive y-axis pointing up (and the x-axis being the "first" and the y-axis the "second" axis) is considered the positive or standard orientation, also called the right-handed orientation.

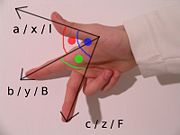
The other way of orienting the axes is following the left hand rule, placing the left hand on the plane with the thumb pointing up.

Regardless of the rule used to orient the axes, rotating the coordinate system will preserve the orientation. Switching the role of x and y will reverse the orientation.

In three dimensions :

The left-handed orientation is shown on the left, and the right-handed on the right.

Once the x- and y-axes are specified, they determine the line along which the z-axis should lie, but there are two possible directions on this line. The two possible coordinate systems which result are called "right-handed" and "left-handed." The standard orientation, where the xy-plane is horizontal and the z-axis points up (and the x- and the y-axis form a positively oriented two-dimensional coordinate system in the xy-plane if observed from above the xy-plane) is called right-handed or positive.

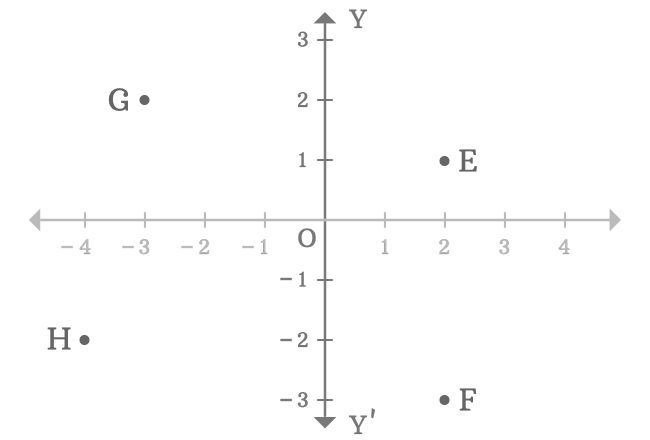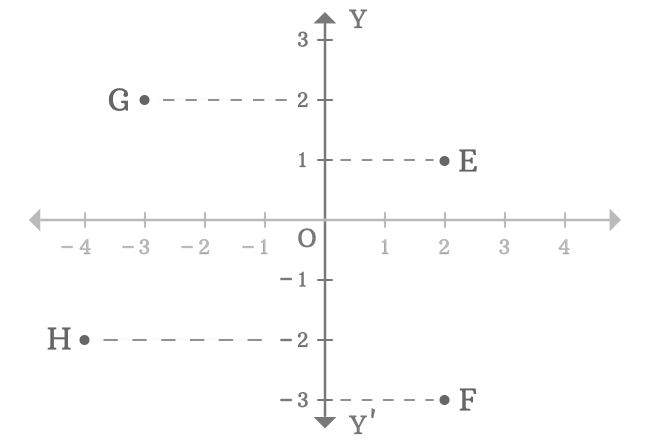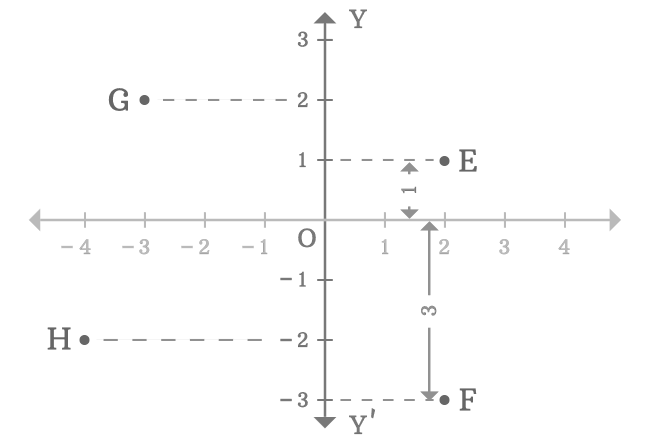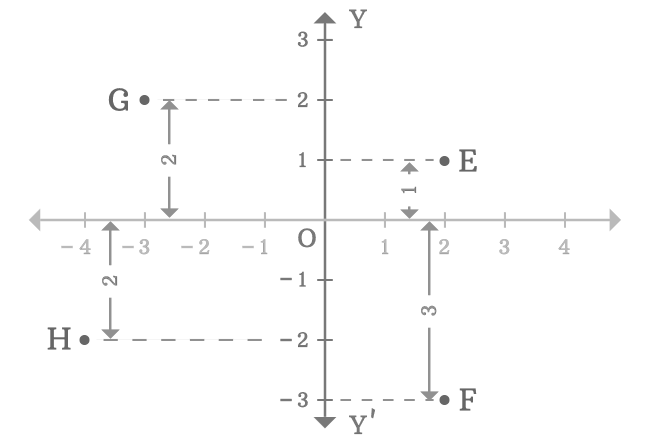
PLOTTING POINTS ON A GRAPH

To plot a point, we need to have two things: a point and a coordinate plane.

Let’s briefly talk about each one.

A Point :

A point in a plane contains two components where order matters! It comes in the form (x,y) where x comes first, and y comes second.

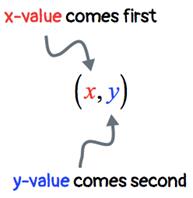
a point is commonly written as (x, y) where the x-value always comes first while the y-value comes second.

Ø The x-value tells how the point moves either to the right or left along the x-axis. This axis is the main horizontal line of the rectangular axis or Cartesian plane.

Ø The y-value tells how the point moves either up or down along the y-axis. This axis is the main vertical line of the rectangular axis or Cartesian plane

Examples of How to Plot Points on a Graph and Identify its Quadrant

Example 1:

Plot the point (4,2) and identify which quadrant or axis it is located.

I will start by placing a dot at the origin which is the intersection of x and y axes. Think of the origin as the “home” where all points come from.

this is an illustration showing the location of the origin on the graph. when plotting points, we start by placing a dot at the origin which is where the x and y-axes intersect.

Next, I will move the dot from the origin 4 units to the right since x = 4 (positive in x-axis means right side movement). Remember, x-value is the first number in the ordered pair (4,2).

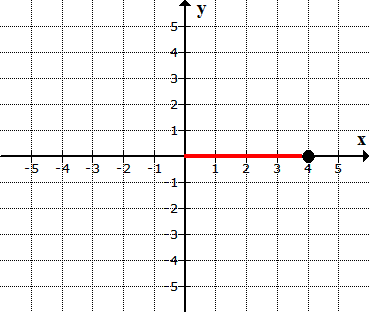
in this illustration, we are shown where to move our pencil or hand from the origin to plot the point (4, 2). since our x-coordinate, which is 4, is positive, we move four units to the right from the origin.

From where I left off, I need to move 2 units going up, parallel to the main vertical axis since y = 2 (positive in y-axis means an upward movement). The y-value is the second number in the ordered pair (4,2).

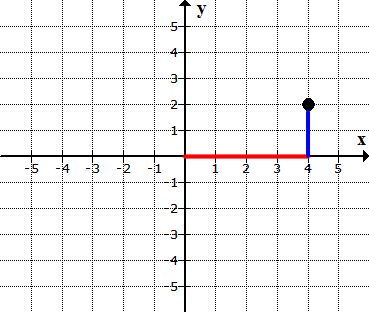
we are shown in this illustration that to plot the point (4,2) on the graph, we then move our hand or pencil upward from positive 4 which is our x-coordinate. this time, we move 2 units up since our y-coordinate which is 2, is positive. this is where you will place your dot.

The final answer should look like this…

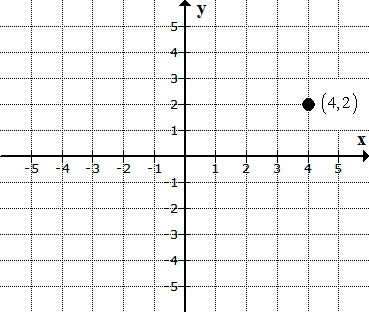
the final location of the point (4, 2) is shown in this graph illustration. after placing the dot, you can write (4,2) to indicate that the point, from the origin, is located 4 units to the right of the origin along the x-axis and 2 units up from point (4,0) along the y-axis.

The point (4,2) is located in Quadrant I.

Example 2:

Plot the point (–5, 4) and identify which quadrant or axis it is located.

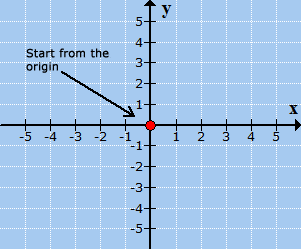
Start by placing a dot at the origin which is known as the center of the Cartesian coordinate axis.

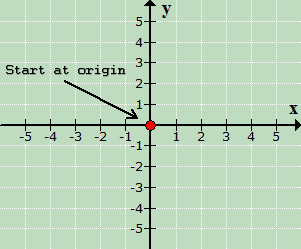
this image illustrates that on a graph, the location of the origin is where our x and y-axes intersect. this is where we should start when trying to plot a point.

From the origin, since x = −5, move 5 units going left.

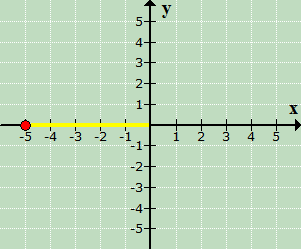
this illustration shows that to plot the point (-5,4), we move five units to the left of the origin, along the x-axis, because our x-coordinate is negative.

…followed by moving the point 4 units up because y = 4.

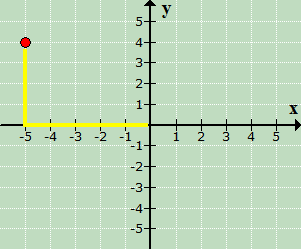
after moving to the left of the origin, we then move 4 units up from the point (-5,0) since our y-coordinate is positive. we then mark our dot here.

This is the final answer. Since the plotted point is in the top left section of the xy-axis, then it must be in Quadrant II.

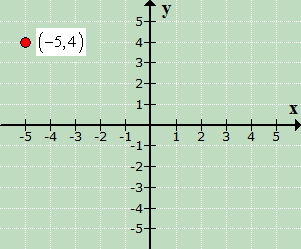
this image illustrates where our point (-5,4) is located on the coordinate plane. as you can see, our dot is located 5 units to the left of the origin along the x-axis and 4 units up from point (-5,0) along the y-axis.

Example 3: Plot the point (5, –3) and identify which quadrant or axis it is located.

Start from the center of the Cartesian plane.

when plotting points, you start at the intersection of the x-axis and y-axis, which is also known as the origin.

Move 5 units to the right since x = 5.

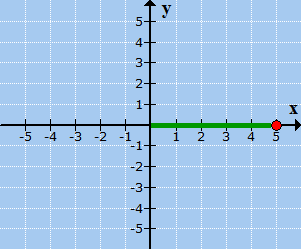
this graph shows that from the origin, we move five units to the right along the x-axis since our x-coordinate, which is 5, is positive.

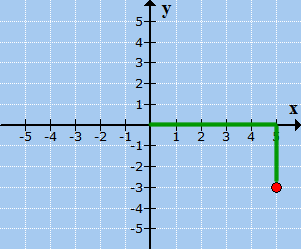
Followed by moving 3 units down since y = −3.

from the point (5,0), we then move 3 units down, since the y-coordinate of the point that we are trying to plot, which is (5,-3), is negative.

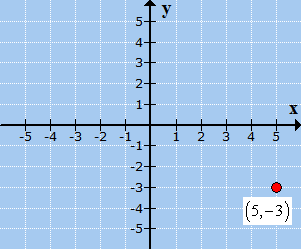
The final plotted point is shown below. Being in the bottom right section of the Cartesian plane, this means that it is in Quadrant IV.

the dot on this graph illustrates our point (5,-3) which is located 5 units to the right from the origin, along the x-axis, and 3 units down along the y-axis from the ordered pair (5,0).

Example 4:

Plot the point (–2, –5) and identify which quadrant or axis it is located.

Place a dot at the origin (center of the xy-axis). Since x = −2, move the point 2 units to the left along the x-axis. Finally, go down 5 units parallel to the y-axis because y = −5.

See the animated solution below.

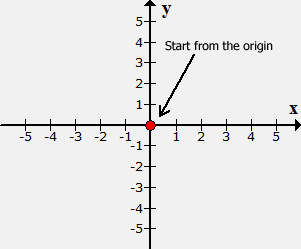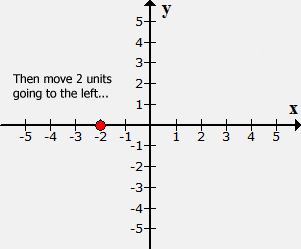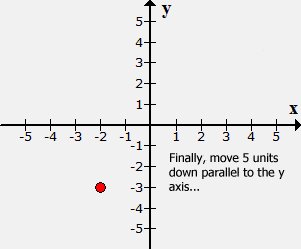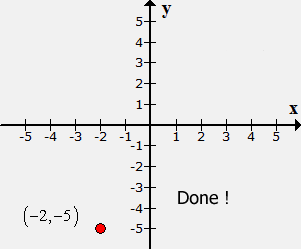
The plotted point is located at the bottom left section of the Cartesian plane. Thus, it is in Quadrant III.

Example 5:

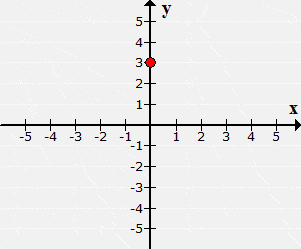
Plot the point (0,3) and identify which quadrant or axis it is located.

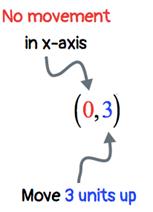
I start by analyzing the given ordered pair. Since x = 0, this means that there is no movement in the x-axis. However, y = 3 implies that I need to move it 3 units in the upward direction.

The plotted point is neither in Quadrant I nor in Quadrant II. To describe its location, we say that it is found along the positive y-axis.

Example 6:

Plot the point (0, –4) and identify which quadrant or axis it is located.

This is very similar to example 5. There will be no movement along the x-axis since x = 0. On the other hand, y = − 4 tells me that I need to move the point from the origin 4 units down.

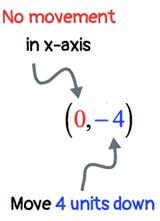
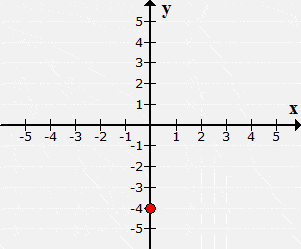
The final point is located neither in Quadrant III nor Quadrant IV. I can claim that it is found along the negative y-axis.

Example 7:

Plot the point (–3,0) and identify which quadrant or axis it is located.

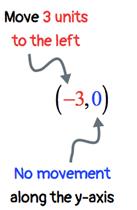
From the origin, I will move it 3 units to the left along the x-axis since x = −3. For y = 0, it means no y-movement will follow.

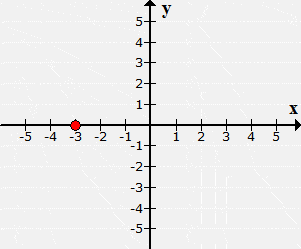
The point is located neither in Quadrant II nor Quadrant III. It is found along the negative x-axis.

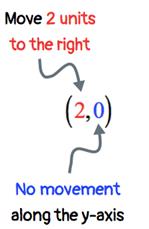
Example 8:

Plot the point (2,0) and identify which quadrant or axis it is located.

With x = 2, I need to move it 2 units to the right. Having y = 0 implies that no y-movement will occur.

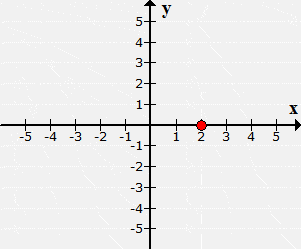
The plotted point is located neither in Quadrant I nor Quadrant IV. It is found along with the positive x-axis.