HERON'S FORMULA

Heron’s formula is used to determine the area of a triangle in geometry. If we know the 3 sides of a triangle, we cancalculate the area of the triangle using this formula.

This area formula makes the calculation of the area of a triangle very easy by eliminating the use of angles and the need to calculate the height of the triangle. The only drawback to this formula is that it demands the length of all 3 sides of the triangle.

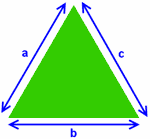
TRIANGLES

A triangle is a 3 sided enclosed figure in geometry. The sum of all the angles of a triangle is 180°. Triangles are basically classified into 3 types depending upon the length of their sides.

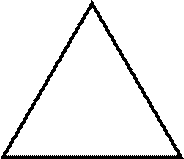
· Equilateral Triangle: 

If all the sides of a triangle are equal in length, then such a triangle is called an equilateral triangle. All angles of an equilateral triangle are equal to 60°. In this figure, we see an equilateral triangle.

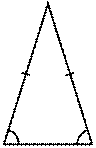
· Isosceles Triangle: 

When any 2 sides of a triangle are equal in length then such a triangle is called an isosceles triangle. In this figure, we see a triangle 2 sides of which are equal in length to one another. The angles of the side opposite to each other are equal in length too.

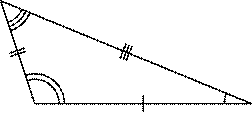
· Scalene Triangle: 

A triangle in which no side is equal in length to the other is called a scalene triangle. No two angles of the triangle are equal in length.

Area of a Triangle from Sides :

You can calculate the area of a triangle if you know the lengths of all three sides, using a formula that has been known for nearly 2000 years.

It is called "Heron's Formula" after Hero of Alexandria (see below)

 Just use this two step process:

Step 1: Calculate "s" (half of the triangles perimeter):

s = a+b+c2

Step 2: Then calculate the Area:

Example:

What is the area of a triangle where every side is 5 long?

Step 1: s = 5+5+52 = 7.5
Step 2: A = √(7.5 × 2.5 × 2.5 × 2.5) = √(117.1875) = 10.825...

1. Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm

Solution:

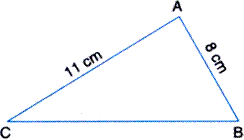
Let the sides of the triangle be a, b and c

Given length of the sides of the triangle are :-

a = 8cm

b = 11cm

c = ?

perimeter of the triangle is given = 32cm

since the sum of all three sides of a triangle is it's perimeter

=> a + b + c = 32cm

=> 8 + 11 + c = 32cm

=> 19 + c = 32cm

=> c = 32 - 19

=> c = 13cm

Now we will find the area of the triangle by heron's formula which is √s(s-a)(s-b)(s-c) where s is the semi-perimeter of the triangle.

semi-perimeter of this triangle = 32/2

= 16cm

area of the triangle = √16(16-8)(16-11)(16-13)

= √(16 × 8 × 5 × 3)

= √(2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 3)

= 2 × 2 × 2√(2 × 5 × 3)

= 8√30cm²

2. A triangular park ABC has sides 120m, 80m and 50m (see Fig. 12.7). A gardener Dhania has to put a fence all around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of Rs 20 per metre leaving a space 3m wide for a gate on one side.

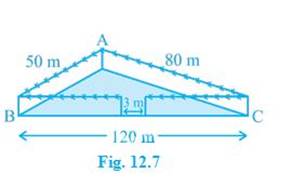
Solution:

Let a=120m b=80m c=50m

s=a+b+c/2

=120+80+50/2

=250/2

=125m

From heron's formula

Area of triangle=√s(s-a)(s-b)(s-c)

=√125*5*45*75

=√5*5*5*5*5*3*3*5*5*3

=375√15m^2
Perimeter of trianglular park=250m

Space left for fencing=250-3

=247m

Cost of fencing 247m=247*20

=Rs.4940

500000+ Question Answers 😊
3. The sides of a triangular plot are in the ratio of 3:5:7 and its perimeter is 300 m. find its area

Solution:

Let the sides of a triangular plot is 3x , 5x and 7x

3x + 5x + 7x = 300 m

15x = 300

x = 300/15

x = 20

then the sides of triangular plot is

3x = (3 × 20) = 60

5x = (5 × 20) = 100

7x = (7 × 20) =140

now the area of triangular plot is area =Let the sides of a triangular plot is 3x , 5x and 7x

3x + 5x + 7x = 300 m

15x = 300

x = 300/15

x = 20

then the sides of triangular plot is

3x = (3 × 20) = 60

5x = (5 × 20) = 100

7x = (7 × 20) =140

now the area of triangular plot is

area =

=

=

Application of Heron’s Formula in Finding Areas of Quadrilaterals

Students of a school staged a rally for a cleanliness campaign. They walked through the lanes in two groups. One group walked through the lanes AB, BC, and CA; where the Other through AC, CD, and DA. Then they cleaned the area enclosed within their lanes.

1. If AB=9m,BC=40m,CD=15m,DA=28m and ∠B = 900, which group cleaned more area and by how much? Find the total area cleaned by the students.

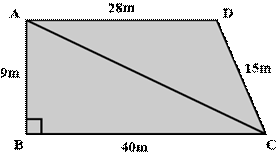
ANSWER

Given, ∠ABC is a right-angled triangle. 

Therefore, AC2=AB2+BC2    ...[Using Pythagoras Theorem]

⇒AC²=9²+40²

⇒AC=81+1600=1681=41m
Area of △ABC=21×base×height

=21×40×9=180m²

Now, in ΔADC,

we have s=228+15+41=284=42m
⇒ Area of ΔDAC =42×(42−28)×(42−15)×(42−41) m²
=42×14×27×1m²
=126m²

So, group 1 covered area ΔABC=180m² and group 2 covered area ΔDAC=126m²
Hence, group 1 covers more area by group 2 which is 54m²=(180m²−126m²) more.
Now, area covered by both the groups =  Area ABC + Area DAC =180m²+126m²=306m²

3. Raghu has a triangular field with sides 240 m, 200 m, 360 m where he grew wheat. In
another triangular field with sides 240 m, 320 m, 400 m adjacent to the previous field, he
wants to grow potatoes and onions. He divided the second field in two parts by joiningthe mid-point of the longest side to the opposite vertex and grew potatoes in one part and
onions in the other part. How much area (in hectares) has been used for wheat, potatoes
and onions?

Solution:

Given:

Length of the triangular field for wheat = 240 m , 200 m , 360 m

Length of the triangular field for potato & onion = 240 m , 320 m , 400 m

To find:

Area of the filed used for Wheat , Potato and Onion .

we use Heron's formula to find area of triangle.

s is semi perimeter  and a , b, c are side,

For first field,

let, a = 240 , b = 200 , c = 360

s = 240+200+360/2 = 800/2 = 400 m

Area of field

1 hector = 10000 m²

So, 16000√2 m² = 22627.4 m² = 2.2 hector

For second field,

let, a = 240 , b = 320 , c = 400

s = 240+320+400/2 = 960/2 = 480 m

Area of field

  Second field is divided in 2 equal areas.

So, Area of Potato = Area of Onion = 19200√3/2 = 9600√3 m² = 16627.69 m² = 1.7 hector

Therefore, Area of the field used for Wheat is 2.2 hector , for Potato is 1.7 hector and for onion is 1.7 hector.