Number systems

Introduction to Natural Numbers

Non-negative counting numbers excluding zero are called Natural Numbers.

N = 1, 2, 3, 4, 5, ……….

Whole Numbers

All natural numbers including zero are called Whole Numbers.

W = 0, 1, 2, 3, 4, 5, …………….

Integers

All natural numbers, negative numbers and 0, together are called Integers.

Z = – 3, – 2, – 1, 0, 1, 2, 3, 4, …………..

Rational Numbers

The number ‘a’ is called Rational if it can be written in the form of r/s where ‘r’ and ‘s’ are integers and s ≠ 0,

Q = 2/3, 3/5, etc. all are rational numbers.

How to find a rational number between two given numbers?

To find the rational number between two given numbers ‘a’ and ‘b’.

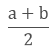
Example:

Find 2 rational numbers between 4 and 5.

Solution:

To find the rational number between 4 and 5

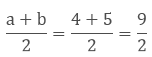
To find another number we will follow the same process again.

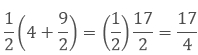
Hence the two rational numbers between 4 and 5 are 9/2 and 17/4.

Remark: There could be unlimited rational numbers between any two rational numbers.

Irrational Numbers

The number ‘a’ which cannot be written in the form of p/q is called irrational, where p and q are integers and q ≠ 0 or you can say that the numbers which are not rational are called Irrational Numbers.

Example - √7, √11 etc.

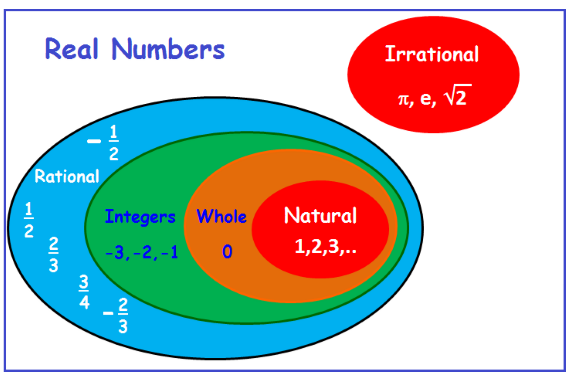
Real Numbers

All numbers including both rational and irrational numbers are called Real Numbers.

R = – 2, – (2/3), 0, 3 and √2

Real Numbers and their Decimal Expansions

1. Rational Numbers

If the rational number is in the form of a/b then by dividing a by b we can get two situations.

a. If the remainder becomes zero

While dividing if we get zero as the remainder after some steps then the decimal expansion of such number is called terminating.

Example:

7/8 = 0.875

b. If the remainder does not become zero

While dividing if the decimal expansion continues and not becomes zero then it is called non-terminating or repeating expansion.

Example:

1/3 = 0.3333….

Hence, the decimal expansion of rational numbers could be terminating or non-terminating recurring and vice-versa.

2. Irrational Numbers

If we do the decimal expansion of an irrational number then it would be non –terminating non-recurring and vice-versa. i. e. the remainder does not become zero and also not repeated.

Example:

π = 3.141592653589793238……

Representing Real Numbers on the Number Line

To represent the real numbers on the number line we use the process of successive magnification in which we visualize the numbers through a magnifying glass on the number line.

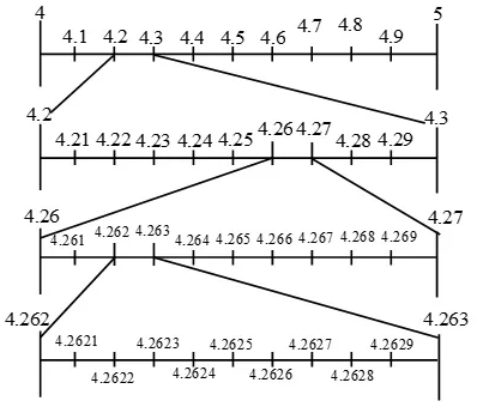
Example:

Step 1: The number lies between 4 and 5, so we divide it into 10 equal parts. Now for the first decimal place, we will mark the number between 4.2 and 4.3.

Step 2: Now we will divide it into 10 equal parts again. The second decimal place will be between 4.26 and 4.27.

Step 3: Now we will again divide it into 10 equal parts. The third decimal place will be between 4.262 and 4.263.

Step 4: By doing the same process again we will mark the point at 4.2626.

Operations on Real Numbers

1. The sum, difference, product and quotient of two rational numbers will be rational.

Example:

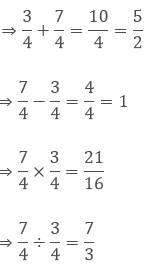
2. If we add or subtract a rational number with an irrational number then the outcome will be irrational.

Example:

If 5 is a rational number and √7 is an irrational number then 5 + √7 and 5 - √7 are irrational numbers.

3. If we multiply or divide a non-zero rational number with an irrational number then also the outcome will be irrational.

Example:

If 7 is a rational number and √5 is an irrational number then 7√7 and 7/√5 are irrational numbers.

4. The sum, difference, product and quotient of two irrational numbers could be rational or irrational.

Example:

Finding Roots of a Positive Real Number ‘x’ geometrically and mark it on the Number Line

To find √x geometrically

1. First of all, mark the distance x unit from point A on the line so that AB = x unit.

2. From B mark a point C with the distance of 1 unit, so that BC = 1 unit.

3. Take the midpoint of AC and mark it as O. Then take OC as the radius and draw a semicircle.

4. From the point B draw a perpendicular BD which intersects the semicircle at point D.

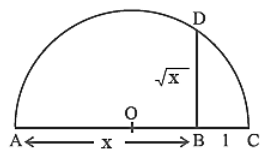
The length of BD = √x.

To mark the position of √x on the number line, we will take AC as the number line, with B as zero. So C is point 1 on the number line.

Now we will take B as the centre and BD as the radius, and draw the arc on the number line at point E.

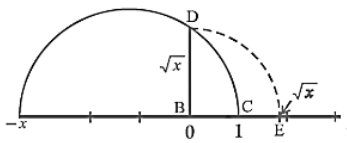
Now E is √x on the number line.

Identities Related to Square Roots

If p and q are two positive real numbers

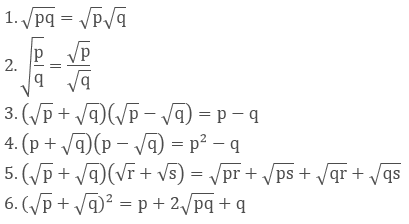
Examples:

1. Simplify

We will use the identity

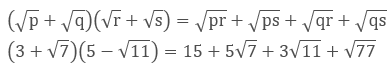
2. Simplify

We will use the identity

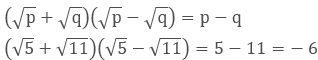
Rationalizing the Denominator

Rationalize the denominator means to convert the denominator containing square root term into a rational number by finding the equivalent fraction of the given fraction.

For which we can use the identities of the real numbers.

Example:

Rationalize the denominator of 7/(7- √3).

Solution:

We will use the identityhere.

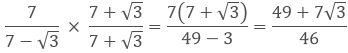
Laws of Exponents for Real Numbers

If we have a and b as the base and m and n as the exponents, then

1. a^m × aⁿ =a^m+n

2. (a^m)ⁿ = a^mn

4. a^m b^m = (ab)^m

5. a⁰ = 1

6. a¹ = a

7. 1/aⁿ = a^-n

· Let a > 0 be a real number and n a positive integer. 

· Let a > 0 be a real number. Let m and n be integers such that m and n have no common factors other than 1, and n > 0. Then,

Example:

Simplify the expression (2x³y⁴) (3xy⁵)².

Solution:

Here we will use the law of exponents

a^m × aⁿ =a^m+n and (a^m)ⁿ = a^mn

(2x³y⁴)(3xy⁵)²

(2x³y⁴)(3 ² x ² y¹⁰)

18. x³. x². y⁴. y¹⁰

18. x³⁺². y⁴⁺¹⁰

18x⁵y¹⁴