Probability

Probability is the study of the uncertainty. The uncertainty of any doubtful situation is measured by means of Probability.

Uses of Probability

Probability is used in many fields like Mathematics, Physical Sciences, Commerce, Biological Sciences, Medical Sciences, Weather Forecasting, etc.

Basic terms related to Probability

1. Randomness

If we are doing an experiment and we don't know the next outcome of the experiment to occur then it is called a Random Experiment.

2. Trial

A trial is that action whose result is one or more outcomes. Like –

· Throw of a dice

· Toss of a coi

3. Independent trial

A trial will be independent if it does not affect the outcome of any other random trial. Like throwing a dice and tossing a coin are independent trials as they do not impact each other.

4. Event

While doing an experiment, an event will be the collection of some outcomes of that experiment.

Example

If we are throwing a dice then the possible outcome for even number will be three i.e. 2, 4, 6. So the event would consist of three outcomes.

Probability – An Experimental Approach

Experimental probability is the result of probability based on the actual experiments. It is also called the Empirical Probability.

In this probability, the results could be different, every time you do the same experiment. As the probability depends upon the number of trials and the number of times the required event happens.

If the total number of trials is ‘n’ then the probability of event D happening is

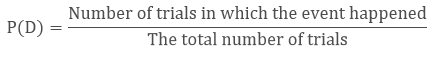
Examples

1. If a coin is tossed 100 times out of which 49 times we get head and 51 times we get tail.

a. Find the probability of getting head.

b. Find the probability of getting tail.

c. Check whether the sum of the two probabilities is equal to 1 or not.

Solution

a. Let the probability of getting head is P(H)

b. Let the probability of getting tail is P(T)

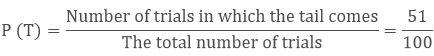
c. The sum of two probability is

= P(H) + P(T)

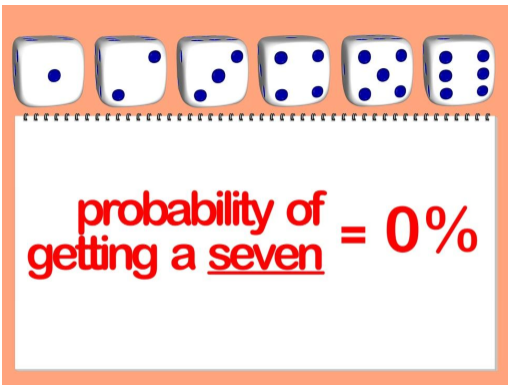
Impossible Events

While doing a test if an event is not possible to occur then its probability will be zero. This is known as an Impossible Event.

Example

You cannot throw a dice with number seven on it.

Sure or Certain Event

While doing a test if there is surety of an event to happen then it is said to be the sure probability. Here the probability is one.

Example: 1

It is certain to draw a blue ball from a bag contain a blue ball only.

This shows that the probability of an event could be

0 ≤ P (E) ≤ 1

Example: 2

There are 5 bags of seeds. If we select fifty seeds at random from each of 5 bags of seeds and sow them for germination. After 20 days, some of the seeds were germinated from each collection and were recorded as follows:

Bag	1	2	3	4	5
No. of seeds germinated	40	48	42	39	41

What is the probability of germination of

(i) more than 40 seeds in a bag?

(ii) 49 seeds in a bag?

(iii) more than 35 seeds in a bag?

Solution:

(i) The number of bags in which more than 40 seeds germinated out of 50 seeds is 3.

P (germination of more than 40 seeds in a bag) =3/5 = 0.6

(ii) The number of bags in which 49 seeds germinated = 0.

P (germination of 49 seeds in a bag) = 0/5 = 0.

(iii) The number of bags in which more than 35 seeds germinated = 5.

So, the required probability = 5/5 = 1.

Elementary Event

If there is only one possible outcome of an event to happen then it is called an Elementary Event.

Remark

If we add all the elementary events of an experiment then their sum will be 1.

The general form

P (H) + P (T) = 1

P (H) + P= 1 (whereis ‘not H’.  

P (H) – 1 = P

P (H) and Pare the complementary events.

Example

What is the probability of not hitting a six in a cricket match, if a batsman hits a boundary six times out of 30 balls he played?

Solution

Let D be the event of hitting a boundary.

So the probability of not hitting the boundary will be

= 0.8