SURFACE AREA AND VOLUME
INTRODUCTION:
Surface
area and volume are calculated for any
three-dimensional geometrical shape. The surface area of any given object is
the area covered or region occupied by the surface of the object. Whereas
volume is the amount of space available in an object. We have learned so far in
geometry about different shapes and sizes such as sphere, cube, cuboid, cone,
cylinder, etc. Each shape has its surface area as well as volume. But in the
case of two-dimensional figures like square, circle, rectangle, triangle, etc.,
AREA
The space
occupied by a two-dimensional flat surface. It is measured in square units.
Generally,
Area can be of two types
Total Surface Area
Curved Surface Area
TOTAL SURFACE AREA:
Total
surface area refers to the area including the base(s) and the curved part.
CURVED SURFACE AREA (LATERAL SURFACE AREA) :
Refers to
the area of only the curved part excluding its base(s).
VOLUME
The
amount of space, measured in cubic units, that an object or substance occupies.
Some shapes are two-dimensional, so it doesn’t have volumes. Example, Volume
of Circle cannot be found, though Volume of the sphere can be. It is
so because a sphere is a three-dimensional shape.
Below
given is the table for
calculating Surface area and Volume for the basic geometrical
figures:
|
Name |
Perimeter |
Total
Surface Area |
Curved
Surface Area |
Volume |
Figure |
|
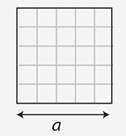
Square |
4a |
a2 |
—- |
—- |
|
|
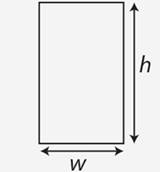
Rectangle |
2(w+h) |
w.h |
—- |
—- |
|
|
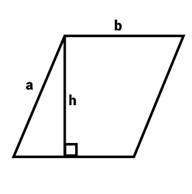
Parallelogram |
2(a+b) |
b.h |
—- |
—- |
|
|
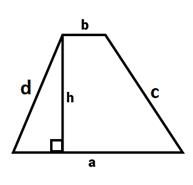
Trapezoid |
a+b+c+d |
1/2(a+b).h |
—- |
—- |
|
|
Circle |
2 π
r |
π r2 |
—- |
—- |
|
|
Ellipse |
2π√(a2 +
b2)/2 |
π a.b |
—- |
—- |
|
|
Triangle |
a+b+c |
1/2
* b * h |
—- |
—- |
|
|
Cuboid |
4(l+b+h) |
2(lb+bh+hl) |
2h(l+b) |
l
* b * h |
|
|
Cube |
6a |
6a2 |
4a2 |
a3 |
|
|
Cylinder |
—- |
2
π r(r+h) |
2πrh |
π r2 h |
|
|
Cone |
—- |
π r(r+l) |
π r
l |
1/3π
r2 h |
|
|
Sphere |
—- |
4 π
r2 |
4π
r2 |
4/3π
r3 |
|
|
Hemisphere |
—- |
3 π
r2 |
2 π
r2 |
2/3π
r3 |
|
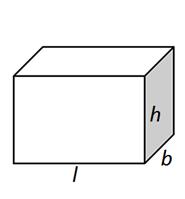
SURFACE AREA OF A CUBOID
AND A CUBE :
Cube: A cube is a three-dimensional
shape which is defined XYZ plane. It has six faces, eight vertices and twelve
edges. All the faces of the cube are in square shape and have equal dimensions.
Cuboids: A cuboids is also a polyhedron having six faces,
eight vertices and twelve edges. The faces of the cuboid are parallel and equal
in dimensions. But not all the faces of a cuboid are equal in dimensions.
SHAPE OF CUBE AND CUBOID
As we already know both cube and cuboid are
in 3D shape, whose axes goes along the
x-axis, y-axis and z-axis plane. Now let us learn in detail.
A cuboid is a closed 3-dimensional geometrical
figure bounded by six rectangular plane regions.
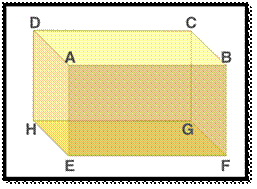
A solid having its length, breadth, height all to
be equal in measurement is called a cube. A cube is a solid bounded by six square plane
regions, where the side of the cube is called edge.
PROPERTIES OF A CUBOID
Let us discuss the properties of cuboid based its
faces, base and lateral faces, edges and vertices.
FACES OF CUBOID :
A Cuboids is made up of six rectangles, each of the
rectangles is called the face. In the figure above, ABFE, DAEH, DCGH, CBFG, ABCD and EFGH are the 6 faces of cuboid.
The top face ABCD and bottom face EFGH form a pair
of opposite faces. Similarly, ABFE, DCGH, and DAEH, CBFG are pairs of
opposite faces. Any two faces other than the opposite faces are
called adjacent
faces.
Consider
a face ABCD, the adjacent face to this are ABFE, BCGF, CDHG, and ADHE.
BASE AND LATERAL FACES :
Any face
of a cuboid may be called as the base of the cuboid. The four faces which are
adjacent to the base are called the lateral faces of the cuboid. Usually,
the surface on which a solid rest on is known to be the base of the solid.
In Figure
(1) above, EFGH represents the base of a cuboid.
EDGES :
The edge
of the cuboid is a line segment between any two adjacent vertices.
There are
12 edges, they are AB,AD,AE,HD,HE,HG,GF,GC,FE,FB,EF and CD and the opposite
sides of a rectangle are equal.
Hence,
AB=CD=GH=EF, AE=DH=BF=CG and EH=FG=AD=BC.
The point
of intersection of the 3 edges of a cuboid is called the vertex of a cuboid.
A cuboid
has 8 vertices A, B, C, D, E, F, G and H represents
vertices of the cuboid in fig 1.
By
observation, the twelve edges of a cuboid can be grouped into three groups such
that all edges in one group are equal in length, so there are three distinct
groups and the groups are named as length, breadth and height.
A cube has three faces and three edges of equal
length.
It has square-shaped faces.
The angles of the cube in the plane are at a right
angle.
Each face of the cube meets four other faces.
Each vertex of the cube meets three faces and three
edges.
Opposite edges of the cube are parallel to each
other.
The
formulas for cube and cuboid are defined based on their surface areas, lateral
surface areas and volume.
SURFACE AREA OF CUBE AND CUBOID
The
surface area of a cuboids is equal to the sum of the areas of its six
rectangular faces.
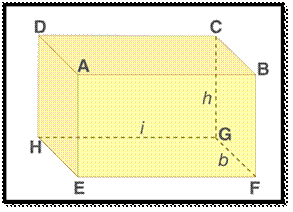
Consider
a cuboid having the length to be ‘l’ cm, breadth be ‘b’ cm and height be ‘h’
cm.
Area of face EFGH = Area of Face ABCD = (l× b)
cm2
Area of face BFGC = Area of face AEHD = (b ×h)
cm2
Area of face DHGC = Area of face ABFE = (l ×h)
cm2
Total
surface area of a cuboid = Sum of the areas of all its 6
rectangular faces
Total
Surface Area of Cuboid= 2(lb + bh +lh)
LATERAL SURFACE AREA OF A CUBOID:
The sum
of surface areas of all sides except the top and bottom face of solid is
defined as the lateral surface area of a solid.
Consider
a Cuboid of length, breadth and height to be l, b and h respectively.
Lateral
surface area of the cuboid= Area of face ADHE + Area of face BCGF + Area of
face ABFE + Area of face DCGH
=2(b × h)
+ 2(l × h)
=2h(l + b)
LSA of Cuboid = 2h(l +b)
SURFACE AREA OF A CUBE:
For cube, length = breadth =
height
Suppose the length of an edge = l
Hence, surface area of the cube =
2(l × l +l × l + l × l) = 2 x 3l2 =
6l2
Total
Surface Area of Cube= 6l2
Lateral surface area of a Cube:
Formula
to find Lateral surface area of the cube is:
2(l × l + l × l) = 4l2
LSA of Cube = 4l2
EXAMPLE 1:
Mary wants to decorate her Christmas tree. She
wants to place the tree on a wooden block covered with coloured
paper with picture of Santa. Claus on it. She must know the exact quantity of
paper to buy for this purpose. If the box has length, breadth and height
as 80cm,40cm and 20cm respectively.
How many square sheets of paper of side 40cm would she require?
ANSWER
Given
that mary wants to paste the
paper on the outer surface of the box. The quantity of the paper required would
be equal to the surface area of the box which is of the shape of cuboid. The
dimension of the box are
Length l=80 cm
Breath b=40 cm
Height h=20 cm
Surface
area of the box =2[lb+bh+hl]
=2[80×40+40×20+20×80]
=2×5600
=11200 cm2
Area
of each sheet of paper =40×40
=1600 cm2
∴ Number of sheets required = 
=7
EXAMPLE
2:
Hameed has a built a cubical water tank with lid
for house, with each outer edge 1.5 m long. He gets the outer surface of the tank
excluding the base, covered with square tiles of side 25 cm. Find how much he would spend for the tiles, if the
cost of tiles is Rs. 360 per dozen.
ANSWER
The length of the each side of water tank =1.5m=150cm
As it
is given that base is not covered with tiles so, five sides of the tank
are covered with tiles.
Therefore,
Surface
area of water tank =5a2=5(150)2=112500 cm2
Side
of tile =25 cm
Area
of tile =252=625 cm2
Number
of tiles to cover five sides of the tank = 
=180
Now,
Cost
of one dozen tiles =Rs.360
Hence,
total cost of 180=
×180=Rs.5400
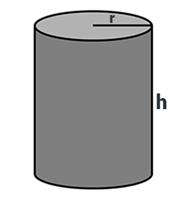
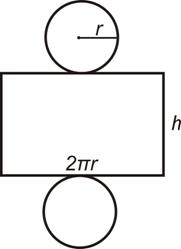
SURFACE AREA OF A RIGHT CIRCULAR CYLINDER
A cylinder is
a solid with congruent circular bases that are in parallel planes. The space
between the circles is enclosed. Just like a circle, the cylinder has a radius
for each of the circular bases.
SURFACE AREA
Surface area is the sum of the areas of the faces. Let’s
find the net of a right cylinder. One way for you to do this is to take a label
off of a soup can or can of vegetables. When you take this label off, we see
that it is a rectangle where the height is the height of the cylinder and the
base is the circumference of the base. This rectangle and the two circular
bases make up the net of a cylinder.
EXAMPLE 1:
Savitri had to
make a model of a cylindrical kaleidoscope for her science project. She wanted
to use chart paper to make the curved surface of the kaleidoscope. What would
be the area of chart paper required by her, if she wanted to make a
kaleidoscope of length 25 cm with a 3.5 cm radius?
You may take (π=722)
ANSWER
Kaleidoscope is of cylindrical shape.
∴ Area
of chart paper required = CSA of cylinder
= 2πrh
= 2×
×3.5×25
= 550 cm2
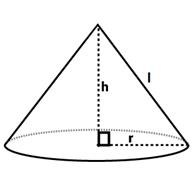
SURFACE AREA OF A RIGHT CIRCULAR CONE :
Cone is defined as a
three-dimensional solid structure that has a circular base. A cone can be
viewed as a set of non-congruent circular disks that are placed over one another
such that the ratio of the radius of adjacent disks remains constant. Consider
a cone as a triangle which is being rotated about one of its vertexes.
Take a paper cone and cut it along its slant height
to observe the figure being formed by the surface of the cone. Mark the two
endpoints as A and B and the point of the intersection of lines as O.
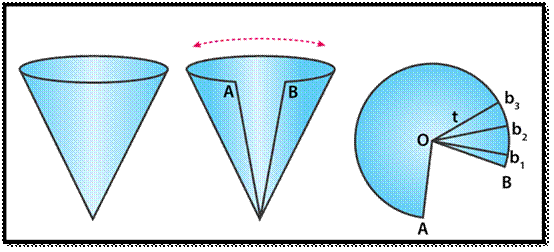
If you further cut this figure into multiple pieces
viz. Ob1, Ob2, Ob3, …….., Obn each measuring the
same length as the slant height of the original cone, you will observe n
triangles are formed out of it. Now, if you try calculating the total area of
this figure, you just need to add an area of these individual triangles. Hence,
Area of figure = (1/2) × (b1 + b2 +
b3 + ………….. + bn)
= (1/2)× (length of an entire curved boundary)
Length
of entire curved boundary = circumference of base = 2π× r (where r is the
radius of the base)
Thus,
area of figure = 1/ 2×2π×r×l=πrl
Hence,
curved surface area of a cone = πrl
Total
Surface Area of a Cone-
The
Total surface area of a cone includes the curved surface as well as area of its
base, which is given as-
Base
Area = πr2
Curved
Surface Area = πrl
Thus
the total surface area is given by-
Πr2+πrl=πr(r+l)
RIGHT CIRCULAR
CONE”:
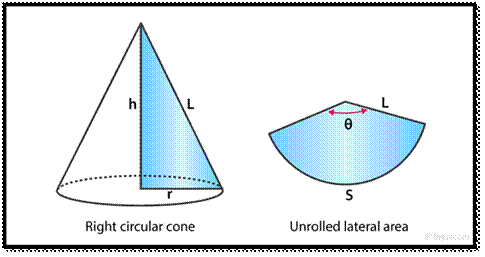
A
circular cone is the one with the circular right section. A Right circular cone
is a circular cone whose axis is perpendicular to the base.
EXAMPLE 1:
Find the curved surface area of a right circular
cone whose slant height is 10 cm and base radius is 7 cm.
ANSWER
Curved surface area =πrl
=×7×10
=220 cm2
EXAMPLE 2:
The height of a cone is 16 cm and its base
radius is 12 cm. Find the curved surface area and the total surface area of the
cone (Use π=3.14).
ANSWER
OA=16cm,AB=l
l=
=
l=20cm
curved surface Area,
C.S.A=πrl=3.14×12×20=753.6cm2
Total surface Area,
T.S.A=πr(r+l)=3.14×12[12+20]=1205.76cm2
EXAMPLE 3:
A Corn Cob, Shaped Somewhat Like A Cone, Has
The Radius Of Its Broadest End As 2.1 Cm And Length (Height) As 20 Cm. If Each 1 Cm2 Of The Surface Of The
Cob Carries An Average Of Four Grains, Find How Many Grains (Approximately) you
would find on the entire cob.
ANSWER
CSA of cone cob = πrl
r=2.1cm,h=20cm
Now, l=
= 
l=
=20.11cm
∴ CSA
of corn cab = ×2.1×20.11=132.73cm2
Number of grains on 1 cm2 of the surface corn cob =4
∴ Number
of grain on 132.73 cm2 of
the surface of corn cab =132.73×4≈531
SURFACE AREA OF A SPHERE
The surface area of a sphere is defined as the
amount of region covered by the surface of a sphere. A Sphere is a
three-dimensional solid object having a round structure, just like a circle.
The difference between a sphere and a circle is that a circle is in
2-dimension, whereas, a sphere is a 3-dimensional
shape.
From a
visual perspective, it has a three-dimensional structure that forms by rotating
a disc that is circular with one of the diagonals. Let us consider an instance
where spherical ball faces are painted. To paint the whole surface, the paint
quantity required has to be known beforehand.
SURFACE AREA OF A
SPHERE FORMULA
The
surface area of a sphere formula is given by,
A = 4 π r2 square
units
For any
three-dimensional shapes, the area of the object can be categorised
into three types. They are
Curved Surface Area
Lateral Surface Area
Total Surface Area
Curved Surface Area: The curved surface area is the
area of all the curved regions of the solid
Lateral Surface Area: `The lateral surface area is the area of all the
regions except bases(i.e., top and bottom)
Total Surface Area: `The total surface area is
the area of all the sides, top and bottom the solid object.
In case
of a Sphere, it has no flat surface
Therefore
the Total surface area of a sphere = Curved surface area of a sphere
EXAMPLE 1:
Find the surface area of a sphere of radius 7
cm.
ANSWER
S=4πr2
r=7 cm
S=4××49=616 cm2.
EXAMPLE 2:
Find the Surface Area And
Total Surface Area Of A Hemisphere Of Radius 21 Cm
ANSWER
Curved Surface area of a hemisphere =2πr2=2××21×21=2772cm2
Total surface area of a hemisphere =3πr2=3××21×21=4158cm2
VOLUME OF CUBOID:
A cuboid is a three-dimensional
structure having six rectangular faces. These six faces of cuboid exist as a
pair of three parallel faces. When the area of the faces of a cuboid is the
same we call this cuboid as a cube. The area of all the faces of a cube is the
same as they are all squares.
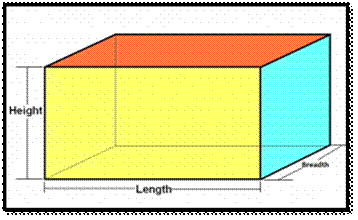
Area and Volume of Cuboid
`The
total surface area of a cuboid is equal to the sum of the areas of the six
rectangular faces whereas the Lateral surface area of a cuboid equal to the sum
of the four rectangular faces, in which two rectangular faces of the and bottom
faces are excluded. The formula for the total surface area and lateral surface area of a cuboid is given as:
Total Surface Area of a Cuboid = 2 (lb+hb+lh) square units
Lateral Surface Area of a Cuboid = 2h (l+b).
Problems on Volume of a Cube and Cuboid
EXAMPLE 1:
A wall of length 10m was to be built across an open ground.
The height of wall is 4m and thickness is 24 cm. If this wall is to be built up
with bricks whose dimensions are 24cm×12cm×8cm, how many bricks would be
required?
Sol:
Length of wall = 10m
Height of wall = 4m
Thickness of wall =
24cm or 0.24m
Volume of wall = Length×breadth×height
= 10×4×0.24 =
9.6 m³
Dimensions of brick =
24cm×12cm×8cm or 0.24m×0.12m×0.08m
Volume of brick
= 0.24m×0.12m×0.08m = 0.002304 m³
Therefore Number of bricks
required = Volume of wall ÷ Volume of 1 brick
= 9.6
m³ ÷ 0.002304 m³
= 4166.66 (approx)
Therefore,Number of bricks required to make the
wall= 4166(approximately)
Volume of cylinder:
The cylinder is a
three-dimensional shape having a circular base. A cylinder can be seen as a set
of circular disks that are stacked on one another. Now, think of a scenario
where we need to calculate the amount of sugar that can be accommodated in a
cylindrical box. In other words, we mean to calculate the capacity or volume of
this box. The capacity of a cylindrical box is basically equal to the volume of
the cylinder involved. Thus, the volume of a three-dimensional shape is
equal to the amount of space occupied by that shape.
Volume of a Cylinder Formula
As a
cylinder can be seen as a collection of multiple congruent disks stacked one
above the other. In order to calculate the space occupied by a cylinder, we
calculate the space occupied by each disk and then add them up. Thus, the
volume of the cylinder can be given by the product of the area of base and
height.
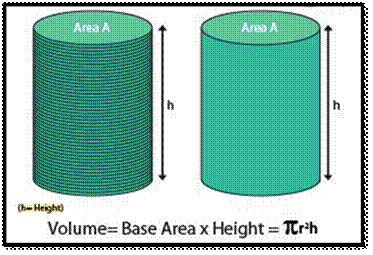
or
any cylinder with base radius ‘r’, and height ‘h’, the volume will be base
times the height.
Therefore,
the cylinder’s volume of base radius ‘r’, and height ‘h’ = (area of base) ×
height of the cylinder
Since
the base is the circle, it can be written as
Volume
= πr2 × h
Therefore, the volume of a cylinder = πr2h cubic
units.
EXAMPLE 1
The pillars of a temple are
cylindrically shaped. If each pillar has a circular base of radius 20 cm and
height 10 m, how much concrete mixture would be required to build 14 such
pillars?
SOL:
Radius of
each pillar = 20 cm = 
Volume of
each pillar = πr2h
= 
3
=
m3
Volume of
14 pillars = 14 
Volume of one pillar
= 14 
m3
= 17.6 m3
So, 14
pillars would need 17.6 m3 of concrete mixture.
EXAMPLE 2:
At a ramzan mela,
a stall keeper in one of the food stalls has a large cylindrical vessel of base
radiusom filled up to a height of 32em with orange
juice. The juice is filled in small cylindrical glasses of radius 3 cm upto a height of 8cm and sold for rs
3 each. How much money does the stall keeper receive by selling the juice
completely?
Answer:
volume
of large cylindrical vessel filled with orange juice =πr2h
=22/7×15×15×32
=22628.57cm3
volume
of small cylindrical glasses filled with orange juice=πr2h
=22/7×3×3×8
=226.29cm3
Number of glasses=Total
number of cylindrical vessel filled with orange juice
volume of small cylindrical glasses
filled with orange juice.
= 22628. 57/226.29
=100 glasses
Sold each for Rs.3 so, 100 glasses of juice will be sold in
= 3×100=300Rs.
VOLUME OF RIGHT CIRCULAR CONE:
A right circular cone is one whose axis is perpendicular to
the plane of the base. We can generate a right cone by revolving a right triangle
about one of its legs.
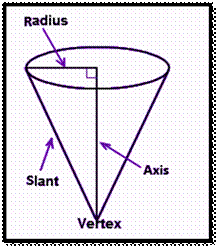
VOLUME OF A RIGHT CIRCULAR CONE
The
volume of a cone is one-third of the product of the area of the base and the
height of the cone. The volume is measured in terms of cubic units.
Volume of
a right circular cone can be calculated by the following formula,
Volume of
a right circular cone = ⅓ (Base area × Height)
Where
Base Area = π r2
Hence,
Volume = ⅓ π r2h
EXAMPLE 1:
The height and slant height of a cone are 21cm and 28cm
respectively, find its volume.
ANSWER:
By Pythagoras theorem,
(slant height)² = (radius
)² + ( height)²
⇒radius² = (28)² - (21)²
= (28 +21) (28- 21)
= 49 × 7
radius = 7√7 cm
now, volume = ( π r² h)/3
=((22/7)× 343× 21)/3
= 7546 cm³
∴ volume = 7546 cm³.
EXAMPLE 2:
Monica has a piece of canvas whose area is 551 m 2 .She
uses itto have a conical tent made, with base radius
of 7 m. Assuming that all the stitching margins and the wastage incurred while
cutting, amounts to approximately 1 m 2 , find the volume of the tent that can
be made with it.
Solution :
[ Take π = 22/7 ]
radius (r) = 7 cm
Curved surface area of the conical tent = Area of the of the canvas - area of the wastage used
= 551 m² - 1 m²
= 550 m²
=> πrl = 550 m²
=22 / 7 
7 l = 550
=> l = ( 550 )/22
=> l = 25 m
h2= l2 –r2
h² = 25² - 7²
=> h² = 625 - 49
=> h² = 576
=> h = √576
=> h = √24²
=> h = 24 m
Volume of a : cone = 1/ 3 I r2 h.
V = (1/3) × (22/7) × 7² × 24
= (22×7×7×24)/(3×7)
= 22×7×8
= 1232 m³
Therefore,
Volume of the conical tent (V) = 1232 m³
VOLUME OF SPHERE:
The volume of sphere is the capacity it has. The
shape of the sphere is round and three -dimensional. It has three axes such as
x-axis, y-axis and z-axis which defines its shape. All the things like football
and basketball are examples of the sphere which have volume. The volume here
depends on the diameter of radius of the sphere, since if we take the
cross-section of the sphere, it is a circle. The surface area of sphere is the area or
region of its outer surface. To calculate the sphere volume, whose radius is
‘r’ we have the below formula:
Volume of a sphere =
4/3 πr3
SPHERE VOLUME
The
sphere is defined as the three-dimensional round solid figure in which every point on its surface is
equidistant from its centre. The fixed distance is called the radius of the
sphere and the fixed point is called the centre of the sphere. When the circle
is rotated, we will observe the change of shape. Thus, the three-dimensional shape sphere is
obtained from the rotation of the two-dimensional object called a circle.
VOLUME OF SPHERE FORMULA
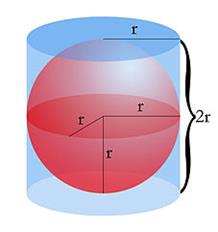
Let,
the volume of the spherical object is assumed to be ⅔ rd of the cylindrical container.
The
Volume of sphere = 2/3 of the volume of the cylinder …….. (1)
It is
observed from the above figure, h = d = 2r
We
know that the volume of a cylinder = πr2h cubic units. ……(2)
Substitute
(2) in (1), we get
The
volume of sphere = (2/3) πr2h …..( 3)
Now,
substitute the value of “h” in (3),
The
volume of sphere = (2/3) πr2 (2r)
It
becomes, V = 4/3 πr3
Therefore, The
volume of a sphere= 4/3 πr3 Cubic units.
Surface Area of Sphere = 4 πr2
EXAMPLE 1:
Find the volume of a sphere of radius 11.2cm
Answer:
Radius = 11.2 cm
Volume of sphere = 4/3 πr3
= 4/3 × 22/7 × (11.2)3
= 88/21 × 1,404.928
= 123,633.66/21
= 5,887.31 cm3.
EXAMPLE 2:
A shotput is
a metallic sphere of radius 4.9 cm. If the density of the metal is 7.8 g. per
cm3, find the mass of the shotput.
ANSWER:
Radius of the shot put = 4.9
cm
Volume of the shot put = (4/3)πr3 cm3
= (4/3) x 22/ 7 x 4.9 x 4.9 x
4.9 cm3
Density of the shot put = 7.8
gm / cm3
Mass of the shot put = 7.8 x
(4/3) x 22/ 7 x 4.9 x 4.9 x 4.9 gm
= 3845.44 gm
= 3.845 kg