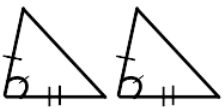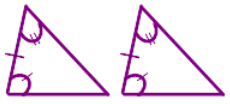Triangles

A closed figure with three sides is called a Triangle. It has three vertex, sides and Angles.

Types of Triangle

1. There are three types of triangles on the basis of the length of the sides.

Name of Triangle	Property	Image
Scalene	Length of all sides are different
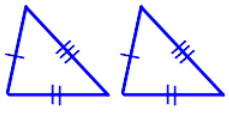
Isosceles	Length of two sides are equal
Equilateral	Length of all three sides are equal

2. There are three types of triangles on the basis of angles.

Name of Triangle	Property	Image
Acute	All the three angles are less than 90°
Obtuse	One angle is greater than 90°
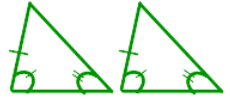
Right	One angle is equal to 90°

Congruence

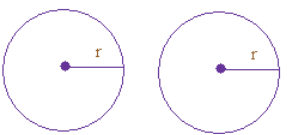
If the shape and size of two figures are same then these are called Congruent.

1. Two circles are congruent if their radii are same.

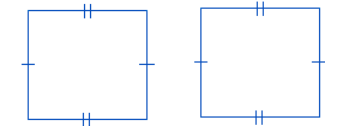
2. Two squares are congruent if their sides are equal.

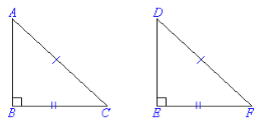
Congruence of Triangles

A triangle will be congruent if its corresponding sides and angles are equal.

The symbol of congruent is “≅”.

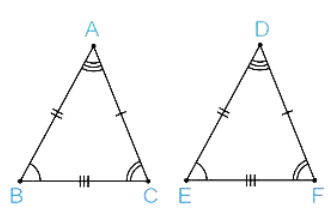
AB = DE, BC = EF, AC = DF

m∠A = m∠D, m∠B = m∠E, m∠C = m∠F

Here ∆ABC ≅ ∆DEF

Criteria for Congruence of Triangles

S.No.	Rule	Meaning	Figure
1.	SAS (Side-Angle-Side) Congruence rule	If the two sides and the including angle of one triangle is equal to another triangle then they are called congruent triangles.
2.	ASA (Angle-Side-Angle) Congruence rule	If the two angles and the including side of one triangle is equal to another triangle then they are called congruent triangles.
3.	AAS (Angle-Angle-Side) Congruence rule	If any two pairs of angles and a pair of the corresponding side is equal in two triangles then these are called congruent triangles.
4.	SSS (Side-Side-Side) Congruence rule	If all the three sides of a triangle are equal with the three corresponding sides of another triangle then these are called congruent triangles.
5.	RHS (Right angle-Hypotenuse-Side) Congruence rule	If there are two right-angled triangles then they will be congruent if their hypotenuse and any one side are equal.

Remark

1. SSA and ASS do not show the congruency of triangles.

2. AAA is also not the right condition to prove that the triangles are congruent.

Example

Find the ∠P, ∠R, ∠N and ∠M if ∆LMN ≅ ∆PQR.

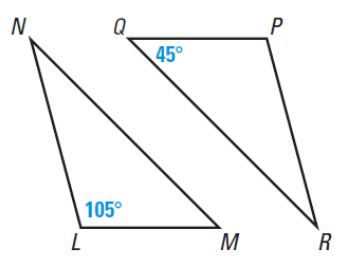
Solution

If ∆ LMN ≅ ∆PQR, then

∠L=∠P

∠M =∠Q

∠N =∠R

So,

∠L=∠P = 105°

∠M =∠Q = 45°

∠M + ∠N + ∠L = 180° (Sum of three angles of a triangle is 180°)

45° + 105° + ∠N = 180°

∠N = 180°- 45° + 105°

∠N = 30°

∠N = ∠R = 30°

Some Properties of a Triangle

If a triangle has two equal sides then it is called an Isosceles Triangle.

1. Two angles opposite to the two equal sides of an isosceles triangle are also equal.

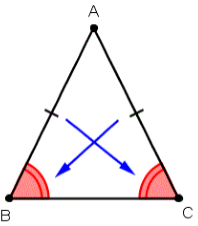
2. Two sides opposite to the equal angles of the isosceles triangle are also equal. This is the converse of the above theorem.

Inequalities in a Triangle

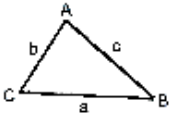
Theorem 1: In a given triangle if two sides are unequal then the angle opposite to the longer side will be larger.

a > b, if and only if ∠A > ∠B

Longer sides correspond to larger angles.

Theorem 2: In the given triangle, the side opposite to the larger angle will always be longer. This is the converse of above theorem.

Theorem 3: The sum of any two sides of a triangle will always be greater than the third side.

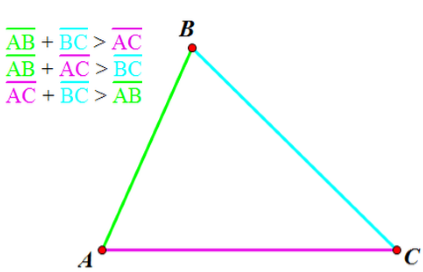
Example

Show whether the inequality theorem is applicable to this triangle or not?

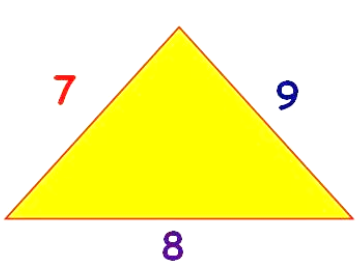
Solution

The three sides are given as 7, 8 and 9.

According to inequality theorem, the sum of any two sides of a triangle will always be greater than the third side.

Let’s check it

7 + 8 > 9

8 + 9 > 7

9 + 7 > 8

This shows that this theorem is applicable to all the triangles irrespective of the type of triangle.