RELATION AND FUNCTION

ORDERED PAIR :

An ordered pair is a composition of the x coordinate (abscissa) and the y coordinate (ordinate), having two values written in a fixed order within parentheses. 

It helps to locate a point on the Cartesian plane for better visual comprehension. 

The numeric values in an ordered pair can be integers or fractions. 

  Ordered Pair = (x,y)

  Where, x = abscissa, the distance measure of a point from the primary axis “x”

  And, y = ordinate, the distance measure of a point from the secondary axis “y”

In the Cartesian plane, we define a two-dimensional space with two perpendicular reference lines, namely x-axis and y-axis. The point where the two lines meet at “0” is the origin.

To Comprehend It Better, Let’s Take An Example. Plot The Point “P” With Coordinates 6, 4. 

As per the definition of ordered pair, the point P will be written as:

P = (6, 4)

The first number in the ordered pair shows the distance from “x" axis which is 6

The second number in the ordered pair shows the distance from “y" axis which is 4

To mark the point on the Cartesian plane, start from the origin. Take 6 steps towards the “x” axis (towards right) starting from the origin. From here, take 4 steps towards the “y” axis (upwards).

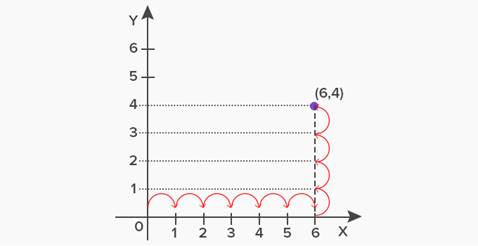
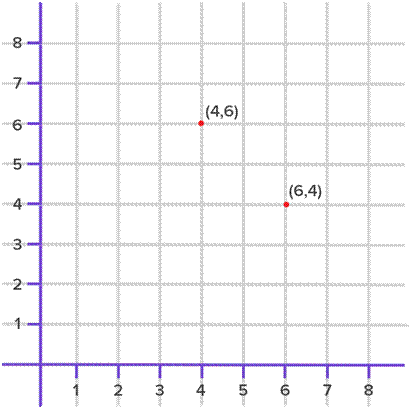
As the name “ordered pair” suggests, the order in which values are written in a pair is very important. The ordered pair (6, 4) is different from the pair (4, 6). Both represent two different points as shown below. 

APPLICATION

The concept of ordered pair is highly useful in data comprehension as well for word problems and statistics. 

The coordinate geometry uses ordered pairs to represent geometric figures and objects in an open space for visual comprehension. Geometric shapes like circle, triangle, square, rectangle and polygons use the ordered pairs to represent the center, vertices and the length of the sides with coordinates. 

CARTESIAN PRODUCT :

Before getting familiar with this term, let us understand what does Cartesian mean. Remember the terms used when plotting a graph paper like axes (x-axis, y-axis), origin etc. For example, (2, 3) depicts that the value on the x-plane (axis) is 2 and that for y is 3 which is not the same as (3, 2).

The way of representation is fixed that the value of the x coordinate will come first and then that for y (ordered way). Cartesian product means the product of the elements say x and y in an ordered way.

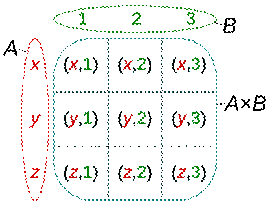
CARTESIAN PRODUCT OF SETS :

The Cartesian products of sets mean the product of two non-empty sets in an ordered way. Or, in other words, the collection of all ordered pairs obtained by the product of two non-empty sets. An ordered pair means that two elements are taken from each set.

For two non-empty sets (say A & B), the first element of the pair is from one set A and the second element is taken from the second set B. The collection of all such pairs gives us a Cartesian product.

The Cartesian product of two non-empty sets A and B is denoted by A × B. Also, known as the cross-product or the product set of A and B. The ordered pairs (a, b) is such that a ∈ A and b ∈ B. So, A × B = {(a,b): a ∈ A, b ∈ B}. For example, Consider two non-empty sets A = {a₁, a₂, a₃} and B = {b₁, b₂, b₃}

Cartesian product A×B = {(a₁,b₁), (a₁,b₂), (a₁,b₃), ( a₂,b₁), (a₂,b₂),(a_2,b₃), (a₃,b₁), (a₃,b₂), (a₃,b₃)}.

It is interesting to know that (a₁,b₁) will be different from (b₁,a₁). If either of the two sets is a null set, i.e., either A = Φ or B = Φ, then, A × B = Φ i.e., A × B will also be a null set

NUMBER OF ORDERED PAIRS :

For two non-empty sets, A and B. If the number of elements of A is h i.e., n(A) = h & that of B is k i.e., n(B) = k, then the number of ordered pairs in Cartesian product will be n(A × B) = n(A) × n(B) = hk.

Question 1:

Let P & Q be two sets such that n(P) = 4 and n(Q) = 2. If in the Cartesian product we have (m,1), (n,-1), (x,1), (y, -1). Find P and Q, where m, n, x, and y are all distinct.

ANSWER:

P = set of first elements = {m, n, x, y} and Q = set of second elements = {1, -1}

Question 2:

What is the Cartesian product used for?

Answer: 

A Cartesian product in computing is basically the exact same as in mathematics. It will be applicable to matrix applications. In SQL it explains a bug where you join two tables wrongly and get many records from one table being connected to each of the records of the other, instead of the expected one.

Question 3:

What is a Cartesian product example?

Answer:

As we know that the Cartesian product is the multiplication of two sets to make the set of all ordered pairs. The first element of the ordered pair will be belonging to the first set and the second pair belong the second set. For instance, Suppose, A = {cow, horse} B = {egg, juice} then, A×B = {(cow, egg), (horse, juice), (cow, juice), (horse, egg)}

Question 4:

What is the Cartesian product of Sets?

Answer:

 The Cartesian product of sets refers to the product of two non-empty sets in an ordered way. Or, in other words, the assortment of all ordered pairs attained by the product of two non-empty sets. An ordered pair basically means that two elements are taken from each set.

THE CARTESIAN PRODUCT OF SETS

1. Let  and  be two sets. The cartesian product of  and , denoted , is the set of all ordered pairs  such that  and .

For example, if  and , then

Graphic presentations can always help to understand; we represent the elements of  as points on an horizontal axis and the elements of  on a vertical axis, as in figure 18. The elements of the cartesian products are then represented by the crossing points of the lattice of parallels to the axes through the points defined above. In Figure , we display a graphical representation for the above example.

Figure 18: The cartesian product of two sets.

“Relations and Functions” is one of the most important topics in algebra. Relations and functions – these are the two different words having different meaning mathematically. You might get confused about their difference. Before we go deeper, let’s understand the difference between both with a simple example.

An ordered pair, represents as (INPUT, OUTPUT): 

Relation shows the relationship between INPUT and OUTPUT. Whereas

A function is a relation which derives one OUTPUT for each given INPUT.

Note: All functions are relations, but not all relations are functions.

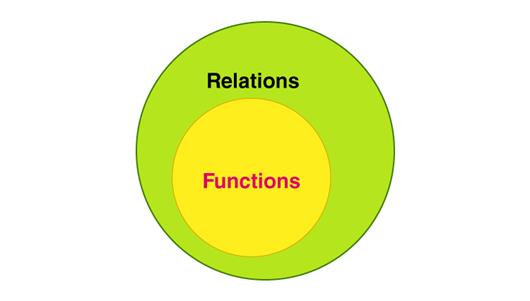
In this section, you will find the basics of the topic – definition of functions and relations,  Special functions, different types of relations and some of the solved examples.

WHAT IS A FUNCTION?

A function is a relation which describes that there should be only one output for each input. OR we can say that, a special kind of relation(a set of ordered pairs) which follows a rule i.e every X-value should be associated to only one y-value is called a Function.

For example:

Domain	Range
-1	-3
1	3
3	9

Let us also look at the definition of Domain and Range of a function.

Domain	It is a collection of the first values in the ordered pairs (Set of all input (x) values).
Range	It is a collection of the second values in the ordered pairs (Set of all output (y) values).

Example:

In the relation, {(-2, 3), {4, 5), (6, -5), (-2, 3)},

The domain is {-2, 4, 6} and Range is {-5, 3, 5}.

Types of Functions

In terms of relations, we can define the types of functions as:

One to one function or Injective function: A function f: P → Q is said to be One to One if for each element of P there is a distinct element of Q.

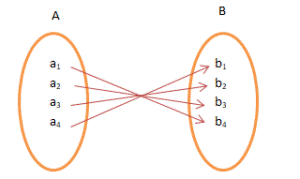
Many to one function: A function which maps two or more elements of P to the same element of set Q.

Onto Function or Surjective function: A function for which every element of set Q there is pre-image in set P

One-one and Onto function or Bijective function: The function f matches with each element of P with a discrete element of Q and every element of Q has a pre-image in P.

Special Functions in Algebra

There are some of the important functions as follow:

Constant Function

Identity Function

Linear Function

Absolute Value Function

Inverse Functions

What is the Relation?

It is a subset of the Cartesian product. Or simply, a bunch of points(ordered pairs).

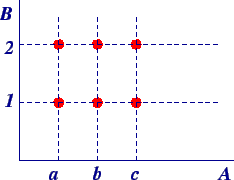
Example:

{(-2, 1), (4, 3), (7, -3)}, usually written in set notation form with curly brackets.

Relation Representation

There are other ways too to write the relation, apart from set notation such as through tables, plotting it on XY- axis or through mapping diagram.

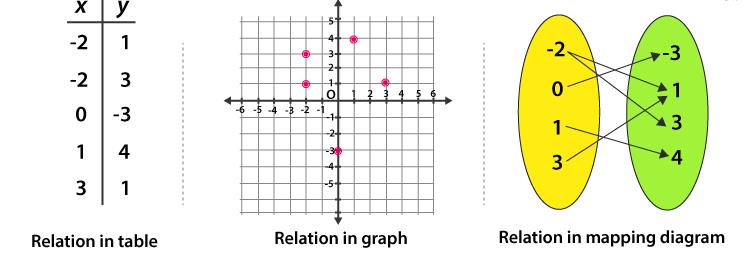
Types of Relations

Different types of relations are as follows:

Empty Relations

Universal Relations

Identity Relations

Inverse Relations

Reflexive Relations

Symmetric Relations

Transitive Relations

Let us discuss all the types one by one.

Empty Relation

When there’s no element of set X is related or mapped to any element of X, then the relation R in A is an empty relation also called as void. I.e R= ∅.

For example,

if there are 100 mangoes in the fruit basket. There’s no possibility of finding a relation R of getting any apple in the basket. So, R is Void as it has 100 mangoes and no apples.

Universal relation

R is a relation in a set, let’s say A is a universal Relation because, in this full relation, every element of A is related to every element of A. i.e R = A × A.

It’s a full relation as every element of Set A is in Set B.

Identity Relation

If every element of set A is related to itself only, it is called Identity relation.

I={(A, A), ∈ a}.

For Example,

When we throw a dice, the outcome we get is 36. I.e (1, 1) (1, 2), (1, 3)…..(6, 6). From these, if we consider the relation(1, 1), (2, 2), (3, 3) (4, 4) (5, 5) (6, 6), it is an identity relation.

Inverse Relation

If R is a relation from set A to set B i.e R ∈ A X B. The relation R−1 = {(b,a):(a,b) ∈ R}.

For Example,

If you throw two dice if R = {(1, 2) (2, 3)}, R−1= {(2, 1) (3, 2)}. Here the domain is the Range R−1 and vice versa.

Reflexive Relation

A relation is a reflexive relation If every element of set A maps to itself. I.e for every a ∈ A,(a, a) ∈ R.

Symmetric Relation

A symmetric relation is a relation R on a set A if (a,b) ∈ R then (b, a) ∈ R, for all a &b ∈ A.

Transitive Relation

If (a,b) ∈ R, (b,c) ∈ R, then (a,c) ∈ R, for all a,b,c ∈ A and this relation in set A is transitive.

Equivalence Relation

If and only if a relation is reflexive, symmetric and transitive, it is called an equivalence relation.

How to convert a Relation into a function?

A special kind of relation(a set of ordered pairs) which follows a rule i.e every X-value should be associated with only one y-value is called a Function.

1. Let A = {5, 6, 7, 8, 9, 10} and B = {7, 8, 9, 10, 11, 13}. Define a relation R from A to B by

R = {(x, y): y = x + 2}. Write down the domain, codomain and range of R.

Answer :

Here, R = {(5, 7), (6, 8), (7, 9), (8, 10), (9, 11)}.

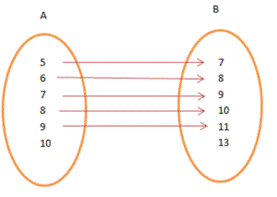
Domain = {5, 6, 7, 8, 9}

Range = {7, 8, 9, 10, 11}

Co-domain = {7, 8, 9, 10, 11, 13}.

Example 1:

Is A = {(1, 5), (1, 5), (3, -8), (3, -8), (3, -8)} a function?

Solution:

 If there are any duplicates or repetitions in the X-value, the relation is not a function.

But there’s a twist here. Look at the following example:

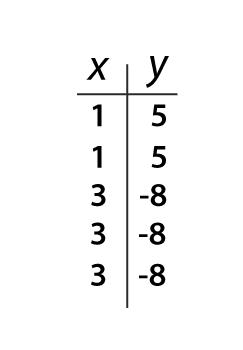
Though X-values are getting repeated here, still it is a function because they are associating with the same values of Y.

The point (1, 5) is repeated here twice and (3, -8) is written thrice. We can rewrite it by writing a single copy of the repeated ordered pairs. So, “A” is a function.

Example 2: 

Give an example of an Equivalence relation.

Solution: 

If we note down all the outcomes of throwing two dice, it would include reflexive, symmetry and transitive relations. that will be called an Equivalence relation.

Example 3:

All functions are relations, but not all relations are functions. Justify.

Solution:

Let’s suppose, we have two relations given in below table

A relation which is not a function	A relation that is a function
As we can see duplication in X-values with different y-values, then this relation is not a function.	As every value of X is different and is associated with only one value of y, this relation is a function

Composite Functions

Suppose f is a function which maps A to B. And there is another function g which maps B to C. Can we map A to C? The mapping of elements of A to C is the basic concept of Composition of functions. When two functions combine in a way that the output of one function becomes the input of other, the function is a composite function.

In mathematics, the composition of a function is a step-wise application. For example, the function f: A→ B & g: B→ C can be composed to form a function which maps x in A to g(f(x)) in C. All sets are non-empty sets. A composite function is denoted by (g o f) (x) = g (f(x)). The notation g o f is read as “g of f”.

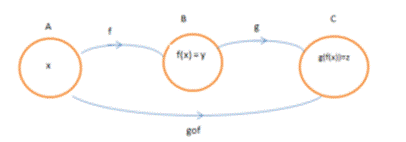
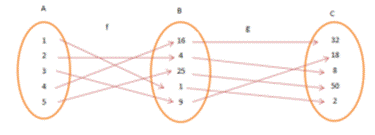
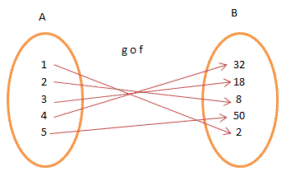
Consider the functions f: A→B and g: B→C. f = {1, 2, 3, 4, 5}→ {1, 4, 9, 16, 25} and g = {1, 4, 9, 16, 25} → {2, 8, 18, 32, 50}. A = {1, 2, 3, 4, 5}, B = {16, 4, 25, 1, 9}, C = {32, 18, 8, 50, 2}.Here, g o f = {(1, 2), (2, 8), (3, 18), (4, 32), (5, 50)}.

The composition of functions is associative in nature i.e., g o f = f o g. It is necessary that the functions are one-one and onto for a composition of functions.

Types of Functions

We have already learned about some types of functions like Identity, Polynomial, Rational, Modulus, Signum, Greatest Integer functions. In this section, we will learn about other types of function.

One to One Function

A function f: A → B is One to One if for each element of A there is a distinct element of B. It is also known as Injective. Consider if a₁ ∈ A and a₂ ∈ B, f is defined as f: A → B such that f (a₁) = f (a₂)

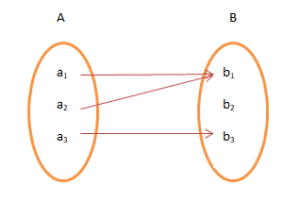
Many to One Function

It is a function which maps two or more elements of A to the same element of set B. Two or more elements of A have the same image in B.

Onto Function

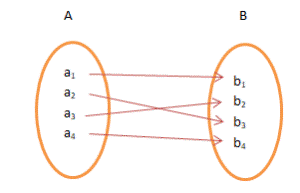
If there exists a function for which every element of set B there is (are) pre-image(s) in set A, it is Onto Function. Onto is also referred as Surjective Function.

One – One and Onto Function

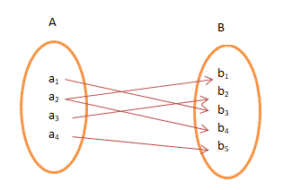
A function, f is One – One and Onto or Bijective if the function f is both One to One and Onto function. In other words, the function f associates each element of A with a distinct element of B and every element of B has a pre-image in A.

What is Bijective Function?

A function is said to be bijective or bijection, if a function f: A → B satisfies both the injective (one-to-one function) and surjective function (onto function) properties. It means that every element “b” in the codomain B, there is exactly one element “a” in the domain A. such that f(a) = b. If the function satisfies this condition, then it is known as one-to-one correspondence.

Bijective Function Properties

A function f: A → B is a bijective function if every element b ∈ B and every element a ∈ A, such that f(a) = b. It is noted that the element “b” is the image of the element “a”, and the element “a” is the preimage of the element “b”. The basic properties of the bijective function are as follows:

While mapping the two functions,i.e., the mapping between A and B (where B need not be different from A) to be a bijection,

each element of A must be paired with at least one element of B,

no element of A may be paired with more than one element of B,

each element of B must be paired with at least one element of A, and

no element of B may be paired with more than one element of A

Bijective Function Example

Example:

Show that the function f(x) = 3x – 5 is a bijective function from R to R.

Solution:

Given Function: f(x) = 3x – 5

To prove:

The function is bijective.

According to the definition of the bijection, the given function should be both injective and surjective.

(i) To Prove:

a. The function is injective

In order to prove that, we must prove that f(a)=c and f(b)=c then a=b.

Let us take,

f(a)=c and f(b)=c

Therefore, it can be written as:

c = 3a-5 and c = 3b-5

Thus, it can be written as:

3a-5 = 3b -5

Simplify the equation; we will get

a = b

Thus, the given function is injective

(ii) To Prove:

The function is surjective

To prove this case, first, we should prove that that for any point “a” in the range there exists a point “b” in the domain s, such that f(b) =a

Let, a = 3x -5

Therefore, b must be (a+5)/3

Since this is a real number, and it is in the domain, the function is surjective.

Thus, the given function satisfies the condition of one-to-one function, and onto function, the given function is bijective.

Hence, proved.

Horizontal Line Test

The horizontal line test is a convenient method that can determine whether a given function has an inverse, but more importantly to find out if the inverse is also a function.

Remember that it is very possible that a function may have an inverse but at the same time, the inverse is not a function because it doesn’t pass the vertical line test.

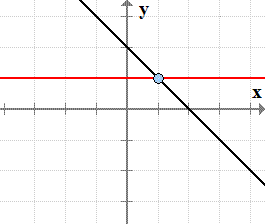
Horizontal Line Cutting or Hitting the Graph at Exactly One Point

• Graph of the line f\left( x \right) = - x + 2f(x)=−x+2.

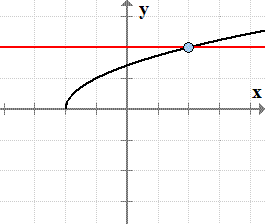
• Graph of the square root function f\left( x \right) = \sqrt {x + 1}f(x)=x+1
  
  

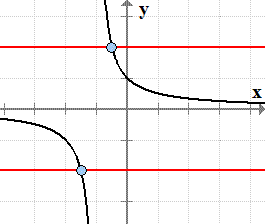
• Graph of the rational function f\left( x \right) = {1 \over {x + 1}}f(x)=x+11.
  
  

On the other hand, if the horizontal line can intersect the graph of a function in some places at more than one point, then the function involved can’t have an inverse that is also a function.

We say this function fails the horizontal line test.

Here are some examples of functions that fail the horizontal line test:

Horizontal Line Cutting or Hitting the Graph at More Than One Point

• Graph of the parabola f\left( x \right) = {x^2} - 2f(x)=x2−2.

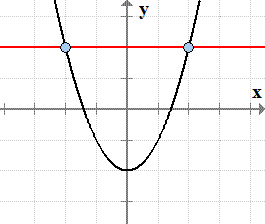
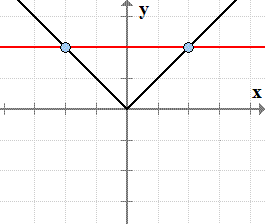
• Graph of absolute value function f\left( x \right) = \left| x \right|f(x)=∣x∣
  
  

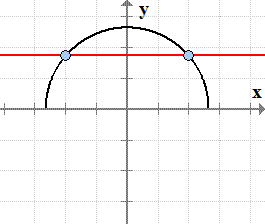
• Graph of semi-circle f(x) = √ (7 - x²} àf(x)=7−x2
  
  

`Special cases of function

There are some special cases of a function which will be very useful. We discuss some of them below

o Constant function

o Identity function

o Real – valued function

(i) Constant function

A function f : A → B is called a constant function if the range of f contains only one element. That is, f (x ) = c , for all x ∈ A and for some fixed c ∈ B.

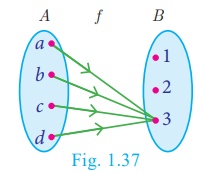
Illustration 16

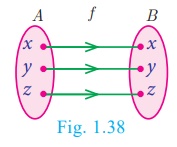
From Fig.1.37, A = {a,b,c,d} and B = {1, 2, 3} and  f  = {(a, 3),(b, 3),(c, 3),(d, 3)} . Since, f (x) = 3 for every x ∈ A ,  Range of  f  = {3} , f  is a constant function.

(ii) Identity function

Let A be a non–empty set. Then the function f: A → A defined by f (x) = x for all x ∈ A is called an identity function on A and is denoted by I_A.

iii) Real valued function

A function f: A → B is called a real valued function if the range of f is a subset of the set of all real numbers R . That is, f (A) ⊆ R.

1. Let f  be a function from R  to R defined by f (x) = 3x − 5 . Find the values of a and b given that (a, 4) and (1, b) belong to f.

Solution 

f (x) = 3x – 5 can be written as f   = {(x, 3x – 5) | x ∈ R}

(a, 4) means the image of a is 4. That is, f (a) = 4

3a – 5 = 4      ⇒ a = 3

(1, b) means the image of 1 is b.

That is, f (1) = b ⇒ b = −2

3(1) – 5 = b  b = –2

2. The distance S (in kms) travelled by a particle in time ‘t’ hours is given by S(t) = [ t² + t ]/2. Find the distance travelled by the particle after

(i) three and half hours.

(ii) eight hours and fifteen minutes.

Solution

The distance travelled by the particle in time t hours is given by 

(i) t = 3.5 hours. Therefore 

The distance travelled in 3.5 hours is 7.875 kms.

t = 8.25 hours. Therefore 

The distance travelled in 8.25 hours is 38.16 kms, approximately.

Composition of Functions

When a car driver depresses the accelerator pedal, it controls the flow of fuel which in turn influences  the speed of the car. Likewise, the  composition  of two functions is a kind of ‘chain reaction’, where the functions act upon one after another (Fig.1.40).

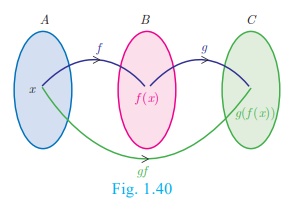
3. We can explain this further with the concept that a function is a ‘process’. If f and g are two functions then the composition g(f (x)) (Fig.1.41) is formed in two steps.

(i) Feed an input (say x) to f ;

(ii) Feed the output f(x) to g to get g(f (x)) and call it gf(x).

Find f  g and g  f when f (x) = 2x + 1 and g(x) = x² – 2

Solution

f (x) = 2x + 1 , g(x) = x² – 2

f  g(x) = f (g(x)) = f (x² − 2) = 2(x² − 2) + 1 = 2x² – 3

g  f (x) = g(f (x)) = g(2x + 1) = (2x + 1)² − 2 = 4x² + 4x – 1

Thus f  g = 2x² − 3, g  f = 4x² + 4x − 1. From the above, we see that f  g ≠ g  f .

Composition of three functions

Let  A,  B,  C,  D  be  four  sets  and let f  : A → B ,   g : B → Cand h  : C → D be three functions. Using composite functions f o g and g o h , we get two new functions like (f o g) o h and f o (g o h).

We observed that the composition of functions is not commutative. The natural question is about the associativity of the operation.

Linear Function

A linear function is a function which forms a straight line in a graph. It is generally a polynomial function whose degree is utmost 1 or 0.  Although the linear functions are also represented in terms of calculus as well as linear algebra. The only difference is the function notation. Knowing an ordered pair written in function notation is necessary too. f(a) is called a function, where a is an independent variable in which the function is dependent. Linear Function Graph has a straight line whose expression or formula is given by;

                                                      y = f(x) = px + q 

Linear Function Graph

Graphing a linear equation involves three simple steps:

1. Firstly, we need to find the two points which satisfy the equation, y = px+q.

2. Now plot these points in the graph or X-Y plane.

3. Join the two points in the plane with the help of a straight line.

The Graph of a Quadratic Function

A quadratic function is a polynomial function of degree 2 which can be written in the general form,

f(x)=ax²+bx+c

Here a, b and c represent real numbers where a≠0.a≠0. The squaring function f(x)=x² is a quadratic function whose graph follows.

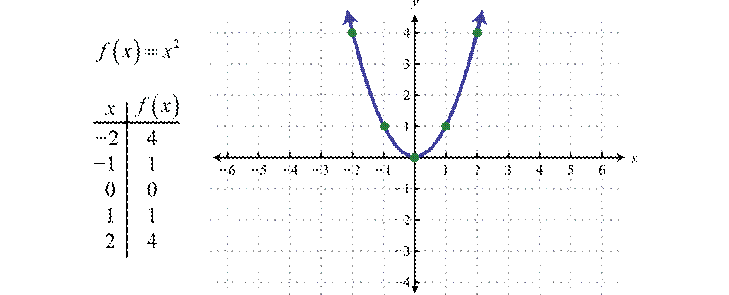
This general curved shape is called a parabola and is shared by the graphs of all quadratic functions. Note that the graph is indeed a function as it passes the vertical line test. Furthermore, the domain of this function consists of the set of all real numbers (−∞,∞ and the range consists of the set of nonnegative numbers [0,∞).

When graphing parabolas, we want to include certain special points in the graph. The y-intercept is the point where the graph intersects the y-axis. The x-intercepts are the points where the graph intersects the x-axis. The vertex is the point that defines the minimum or maximum of the graph. Lastly, the line of symmetry (also called the axis of symmetry) is the vertical line through the vertex, about which the parabola is symmetric.

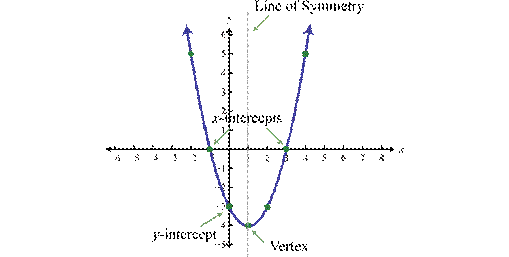
For any parabola, we will find the vertex and y-intercept. In addition, if the x-intercepts exist, then we will want to determine those as well. Guessing at the x-values of these special points is not practical; therefore, we will develop techniques that will facilitate finding them. Many of these techniques will be used extensively as we progress in our study of algebra.

Given a quadratic function f(x)=ax²+bx+c, find the y-intercept by evaluating the function where x=0. In general,  f(0)=a(0)²+b(0)+c=c, and we have

y-intercept      (0,c)

Next, recall that the x-intercepts, if they exist, can be found by setting f(x)=0. Doing this, we have a²+bx+c=0, which has general solutions given by the quadratic formula, x=−b±b²−4ac√2a. Therefore, the x-intercepts have this general form: