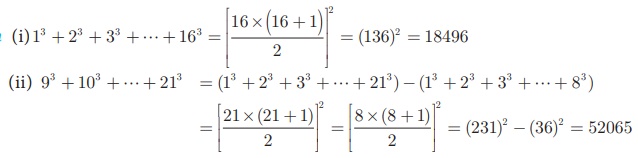NUMBERS AND SEQUENCE

INTRODUCTION:

A number is an arithmetic value used for representing the quantity and used in making calculations. A written symbol like “3” which represents a number is known as numerals. A number system is a writing system for denoting numbers using digits or symbols in a logical manner. The numeral system:

Represents a useful set of numbers

Reflects the arithmetic and algebraic structure of a number

Provides standard representation

Euclid’s Division Lemma:

According to Euclid’s Division Lemma if we have two positive integers a and b, then there exist unique integers q and r which satisfies the condition a = bq + r where 0 ≤ r ≤ b.

The basis of the Euclidean division algorithm is Euclid’s division lemma. To calculate the Highest Common Factor (HCF) of two positive integers a and b we use Euclid’s division algorithm. HCF is the largest number which exactly divides two or more positive integers. By exactly we mean that on dividing both the integers a and b the remainder is zero.

Euclid’s Division Lemma Algorithm

Consider we have two numbers 78 and 980 and we need to find the HCF of both of these numbers. To do this, we choose the largest integer first, i.e. 980 and then according to Euclid Division Lemma, a = bq + r where 0 ≤ r ≤ b;

980 = 78 × 12 + 44

Now, here a = 980, b = 78, q = 12 and r = 44.

Now consider the divisor as 78 and the remainder 44 and apply the Euclid division method again, we get

78 = 44 × 1 + 34

Similarly, consider the divisor as 44 and the remainder 34 and apply the Euclid division method again, we get

44 = 34 × 1 + 10

Following the same procedure again,

34 = 10 × 3 + 4

10=4×2+2

4=2×2+0

As we see that the remainder has become zero, therefore, proceeding further is not possible and hence the HCF is the divisor b left in the last step which in this case is 2. We can say that the HCF of 980 and 78 is 2.

Let us try another example to find the HCF of two numbers 250 and 75. As the larger the integer is 250, therefore, applying Euclid Division Lemma a = bq + r where 0 ≤ r ≤ b, we have

a = 250 and b = 75

⇒ 250 = 75 × 3 + 25

Applying the Euclid’s Division Algorithm again we have,

75 = 25 × 3 + 0

As the remainder becomes zero, we cannot proceed further. According to the algorithm, in this case the divisor is 25 and hence, the HCF of 250 and 75 is 25.

EXAMPLE

1. Show that the square of any odd integer is of the form 4q + 1 for some integer q:

By division algorithm we know here

0 ≤ r < 4 , So r = 0, 1, 2, 3.

When r = 0

a = 4m

Squaring both side , we get

a² = ( 4m )²

a² = 4 ( 4m²)

a² = 4q , where q = 4m²

When r = 1

a = 4m + 1

squaring both side , we get

a² = ( 4m + 1)²

a² = 16m² + 1 + 8m

a² = 4 ( 4m² + 2m ) + 1

a² = 4q + 1 , where q = 4m² + 2m

When r = 2

a = 4m + 2

Squaring both hand side , we get

a² = ( 4m + 2 )²

a² = 16m² + 4 + 16m

a² = 4 ( 4m² + 4m + 1 )

a² = 4q , Where q = 4m² + 4m + 1

When r = 3

a = 4m + 3

Squaring both hand side , we get

a² = ( 4m + 3)²

a² = 16m² + 9 + 24m

a² = 16m² + 24m + 8 + 1

a² = 4 ( 4m² + 6m + 2) + 1

a² = 4q + 1 , where q = 4m² + 6m + 2

THEOREM:

Let a & b are two positive integers such that a=bq+r. Prove that the common factor of a & b must be the common factor of b & r. 

ANSWER:

a=bq+r

Let a common factor of 'a' and 'b' be 'c'.

So a=cA and b=cB, where 'A' and 'B' are integers.

Substituting these values in the first equation, we get

cA = cBq + r

In the left hand side we have a multiple of 'c'. Hence, the right hand side should also be a multiple of 'c'.

cBq is a multiple of 'c'. So for 'cBq + r' to be a multiple of 'c', the second term 'r' must be a multiple of 'c'.

Hence, we can write 'r' as cR, where 'R' is some integer. 

Hence, 'c' is a common factor of 'b' and 'r'. (Proved)

EXAMPLE:

Find the HCF of 155 and 1385 by Eulcid's Algorithm and express it in a linear. combination of two numbers

By applying Euclid's Division Algorithm, we get

1385 = 155 × 8 + 145

Here the remainder (145) ≠ 0

155 = 145 × 1 + 10

Here the remainder (10) ≠ 0

145 = 10 × 14 + 5

Here the remainder (5) ≠ 0

10 = 5 × 2 + 0

Therefore HCF(155, 1385) = 5

Find the greatest number that will divide 445, 572 and 699 leaving reamainder 4, 5and 6 respectively:

Solution:

445 - 4 = 441 

                 572 - 5 = 567 

                 699 - 6 = 693 

Now find the greatest common factor of those 3 numbers: 

441 = 3 x 3 x 7 x 7 

572 = 3 x 3 x 3 x 3 x 7 

693 = 3 x 3 x 7 x 11 

The common factors are 3 x 3 x 7 = 63 

HCF Of (441,567,693) = 63 

445 / 63 = 7 remainder 4 

572 / 63 = 9 remainder 5 

699 / 63 = 11 remainder 6 

Fundamental Theorem of Arithmetic:

Fundamental Theorem of Arithmetic states that every integer greater than 1 is either a prime number or can be expressed in the form of primes. In other words, all the natural numbers can be expressed in the form of the product of its prime factors. To recall, prime factors are the numbers which are divisible by 1 and itself only. For example, the number 35 can be written in the form of its prime factors as:

35 = 7 × 5

Here, 7 and 5 are the prime factors of 35

Similarly, another number 114560 can be represented as the product of its prime factors by using prime factorization method,

114560 = 2⁷ × 5 × 179

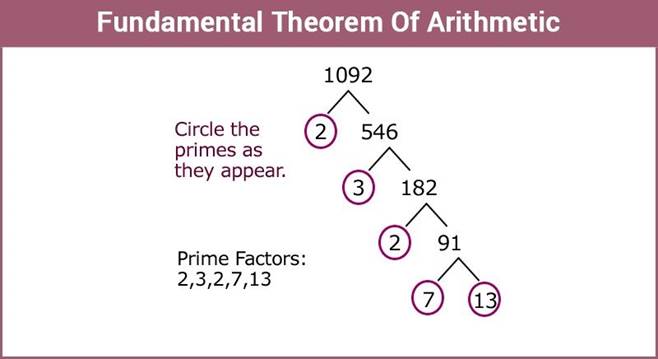
Proof for Fundamental Theorem of Arithmetic

In number theory, a composite number is expressed in the form of the product of primes and this factorization is unique apart from the order in which the prime factor occurs.

From this theorem we can also see that not only a composite number can be factorized as the product of their primes but also for each composite number the factorization is unique, not taking into consideration order of occurrence of the prime factors.

In simple words, there exists only a single way to represent a natural number by the product of prime factors. This fact can also be stated as:

The prime factorization of any natural number is said to be unique for except the order of their factors.

In general, a composite number “a” can be expressed as,

a = p₁ p₂ p₃ ………… p_n, where p₁, p₂, p₃ ………… p_n are the prime factors of a written in ascending order i.e. p₁≤p₂≤p₃ ………… ≤p_n.

Significance of the Fundamental Theorem of Arithmetic :

Every composite number can be expressed (factorised ) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur.

This theorem also says that the prime factorisation of a natural number is unique, except for the order of its factors.

For example 20 can be expressed as 2×2×52×2×5

Using this theorem the LCM and HCF of the given pair of positive integers can be calculated.

LCM = Product of the greatest power of each prime factor, involved in the numbers.

HCF = Product of the smallest power of each common prime factor in the numbers.

EXAMPLE:

Can The Number 6n,n being a natural number,end with digit 5?give reasons.

ANSWER:

Consider the number 6n , for n a natural number.

A number ending with digit 5, must be divisible by 5.

But 6 x 5 =30.

So 6 multiplied by any multiple of 5 has last digit zero.

so the last digit of 6n can never be 5.

EXAMPLE:

Is 7×5×3×2+3 a composite number?Justify your answer

ANSWER:

The said number will be a composite number, since the product 7×5×3×2 is divisible by 3 so the number 7×5×3×2 +3 will also be divisible by 3 hence it would be a composite number.  

Also, If we will divide 7×5×3×2 by 3 the answer will simply be 7×5×2, next we will consider the multiplication 3 (7×5×2+1) the answer will be 7×5×3×2+3 hence this number has factor other than one.

Thus, in common from the given expression 7×5×3×2 +3 will be written as -   = 3 (7×5×2+1) which proves the fact that 7×5×3×2+3 is a composite number

= 7 × 5 × 3 × 2 + 3 = 3(7 × 5 × 2 + 1)

= 3 ( 70+1)

= 3 × 71

Since, it has two factors other than itself and one, thus it is a composite number.

EXAMPLE:

Two positive integers a and b are such that a + b = (a/b) + (b/a). What is the value of a² + b²?

ANSWER:

a+b=a/b+b/a

-> Now take L.C.M

a+b=(a²+b²)/ab

-> Cross multiplying

(a+b)ab=a²+b²

a².b+b².a= a²+b²

Take a² and b² common

a²(b−1)+b²(a−1)=0 --(1)

Now since a and b are positive integers - their square can’t be zero.

So in order to make the equation 1 equal to zero:

(b−1) and (a−1)both has to be 0.

Therefore,

b−1=0 =>b=1

and,

a−1=0 =>a=1

Hence a=b=1

Thus

a²+b²=1²+1²

 =2

Modular Arithmetic:

When we divide two integers we will have an equation that looks like the following:

{A}/{B} = Q { remainder } RBA=Q remainder Rstart fraction, A, divided by, B, end fraction, equals, Q, start text, space, r, e, m, a, i, n, d, e, r, space, end text, R

AAA is the dividend
BBB is the divisor
QQQ is the quotient
RRR is the remainder

Sometimes, we are only interested in what the remainder is when we divide AAA by BBB.
For these cases there is an operator called the modulo operator (abbreviated as mod).

Using the same AAA, BBB, QQQ, and RRR as above, we would have: A { mod } B = RA mod B=RA, start text, space, m, o, d, space, end text, B, equals, R

We would say this as AAA modulo BBB is equal to RRR. Where BBB is referred to as the modulus.

For example:

13513 mod 5==2 remainder 33

Visualize modulus with clocks

Observe what happens when we increment numbers by one and then divide them by 3.

03132333435363=======0 remainder 00 remainder 10 remainder 21 remainder 01 remainder 11 remainder 22 remainder 0

The remainders start at 0 and increases by 1 each time, until the number reaches one less than the number we are dividing by. After that, the sequence repeats.

By noticing this, we can visualize the modulo operator by using circles.

We write 0 at the top of a circle and continuing clockwise writing integers 1, 2, ... up to one less than the modulus.

For example, a clock with the 12 replaced by a 0 would be the circle for a modulus of 12.

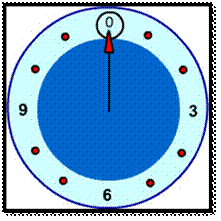
To find the result of A { mod } BA mod BA, start text, space, m, o, d, space, end text, B we can follow these steps:

1. Construct this clock for size BBB

2. Start at 0 and move around the clock AAA steps

3. Wherever we land is our solution.

(If the number is positive we step clockwise, if it's negative we step counter-clockwise.)

Connecting Euclid’s Division lemma and Modular Arithmetic

Let m and n be integers, where m is positive. Then by Euclid’s division lemma, we can write n = mq + r  where  0 ≤ r  < m  and q is an integer. Instead of writing n = mq + r we can use the congruence notation in the following way.

We say that n is congruent to r modulo m, if n = mq + r for some integer q.

n = mq + r

n–r = mq

n–r≡0 (mod m) 

n≡r (mod m)

Thus the equation n = mq + r through Euclid’s Division lemma can also be written n ≡ r (mod m).

 Modulo operations:

Similar to basic arithmetic operations like addition, subtraction and multiplication performed on numbers we can think of performing same operations in modulo arithmetic. The following theorem provides the information of doing this.

Example :

Find the remainders when 70004 and 778 is divided by 7.

Solution

Since 70000 is divisible by 7

70000   ≡ 0 (mod 7)

70000 + 4≡ 0 + 4 (mod 7)

70004 ≡ 4 (mod 7)

 Therefore, the remainder when 70004 is divided by 7 is 4

Since 777 is divisible by 7

777 ≡ 0 (mod 7)

777 + 1 ≡ 0 + 1 (mod 7)

778 ≡ 1 (mod 7)

Therefore, the remainder when 778 is divided by 7 is 1.

Example:

Determine the value of d such that 15 ≡ 3 (mod d).

Solution

15 ≡ 3 (mod d) means 15 − 3 = kd, for some integer k.

12 = kd.

gives d divides 12.

The divisors of 12 are 1,2,3,4,6,12. But d should be larger than 3 and so the possible values for d are 4,6,12.

 Example 3:

Find the least positive value of x such that

(i) 67 + x ≡ 1 (mod 4)

(ii) 98 ≡ (x + 4) (mod 5)

Solution

(i) 67 + x ≡ 1 (mod 4)

67 + x – 1 = 4n , for some integer n

66 + x = 4n

66 + x is a multiple of 4.

Therefore, the least positive value of x must be 2, since 68 is the nearest multiple of 4 more than 66.

(ii) 98 ≡ (x + 4) (mod 5)

98 − (x + 4) = 5n , for some integer n.

94 - x = 5n

94 - x is a multiple of 5.

Therefore, the least positive value of x must be 4

Since 94 − 4 = 90 is the nearest multiple of 5 less than 94.

Example :

Solve 8x ≡ 1 (mod 11)

Solution

8x ≡ 1 (mod 11) can be written as 8x − 1 = 11k, for some integer k.

x = (11k + 1) / 8

When we put k = 5, 13, 21, 29,... then 11k+1 is divisible by 8.

x = = (11× 5 + 1) /8=  7

= (11 × 13 + 1)/8 = 18

Therefore, the solutions are 7,18,29,40, …

Example :

Compute x, such that 10⁴ ≡ x (mod 19)

Solution

10² = 100 ≡ 5 (mod 19)

10⁴ = (10² )² ≡ 5² (mod 19)

 10⁴ ≡ 25 104 ≡ 25

10⁴ ≡ 6 (mod 19) (since 25  6(mod 19))

Therefore, x = 6.

Example :

Find the number of integer solutions of 3x ≡ 1 (mod 15).

Solution

3x ≡ 1 (mod 15) can be written as

3x − 1 = 15k for some integer k

3x = 15k + 1

x = [15k + 1] / 3

x = 5k + 1/3

Since 5k is an integer, 5k + (1/3) cannot be an integer.

So there is no integer solution.

Example :

A man starts his journey from Chennai to Delhi by train. He starts at 22.30 hours on Wednesday. If it takes 32 hours of travelling time and assuming that the train is not late, when will he reach Delhi?

Solution

Starting time 22.30, Travelling time 32 hours. Here we use modulo 24.

The reaching time is

22.30+32 (mod 24) ≡ 54.30 (mod24) 

                          ≡ 6.30 (mod24)

(Since 32 = (1×24)  +   8 Thursday Friday)

Thus, he will reach Delhi on Friday at 6.30 hours.

Example :

Kala and Vani are friends. Kala says, “Today is my birthday” and she asks Vani, “When will you celebrate your birthday?” Vani replies, “Today is Monday and I celebrated my birthday 75 days ago”. Find the day when Vani celebrated her birthday.

Solution

Let us associate the numbers 0, 1, 2, 3, 4, 5, 6 to represent the weekdays from Sunday to Saturday respectively.

Vani says today is Monday. So the number for Monday is 1. Since Vani’s birthday was 75 days ago, we have to subtract 75 from 1 and take the modulo 7, since a week contain 7 days.

–74 (mod 7) ≡ –4 (mod 7) ≡ 7–4 (mod 7) ≡ 3 (mod 7)

(Since, −74 – 3 = −77 is divisible by 7)

Thus, 1 − 75 ≡ 3 (mod 7)

The day for the number 3 is Wednesday.

Therefore, Vani’s birthday must be on Wednesday

SEQUENCES

Consider the following pictures

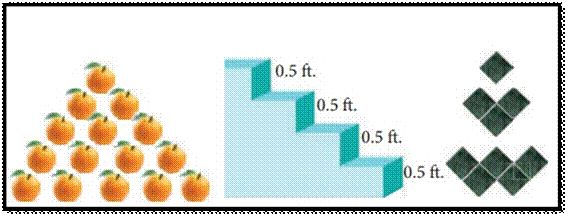
here is some pattern or arrangement in these pictures. In the first picture, the first row contains one apple, the second row contains two apples and in the third row there are three apples etc... The number of apples in each of the rows are 1, 2, 3, ... 

In the second picture each step have 0.5 feet height. The total height of the steps from the base are 0.5 feet,1 feet, 1.5 feet,... In the third picture one square, 3 squares, 5 squares, ....

These numbers belong to category called “Sequences”.

Illustration

1. 1,3,5,7,... is a sequence with general term a_n = 2n − 1 . When we put n = 1, 2, 3,..., we get a₁ =1, a₂ = 3, a₃ = 5, a₄ = 7,...

2. 1/2 , 1/3 , 1/4 , 1/5 ,... is a sequence with general term 1/ [n + 1] . When we put n = 1,2,3,.... we get

a₁  = 1/2 ,  a₂  = 1/3 , a₃  = 1/4 , a₄  = 1/5 ,...

If the number of elements in a sequence is finite then it is called a Finite sequence.  If the number of elements in a sequence is infinite then it is called an Infinite sequence

SEQUENCE AS A FUNCTION

A sequence can be considered as a function defined on the set of natural numbers N. In particular, a sequence is a function f : N → R , where R is the set of all real numbers.

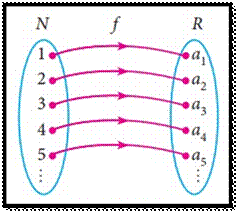
If the sequence is of the form a₁,a₂,a₃,...  then we can associate the function to the sequence a₁,a₂,a₃,... by f (k) = a_k , k = 1,2,3,...

Example :

Find the next three terms of the sequences

(i) 1/16 , 1/6 ,  1/14 , . . . .  (ii) 5, 2,- 1, -4,. . . . (iii) 1, 0.1, 0.01,. . .

Solution

(i)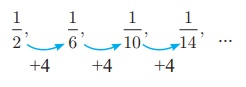 

In the above sequence the numerators are same and the denominator is increased by 4.

So the next three terms are

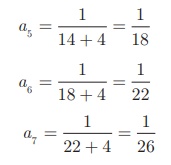
(ii)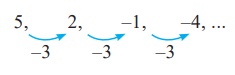 

Here each term is decreased by 3. So the next three terms are -7,  -10,  -13 .

(iii)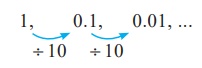 

Here each term is divided by 10. Hence, the next three terms are

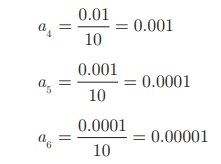
Example :

The general term of a sequence is defined as

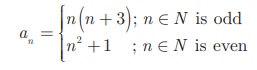
Find the eleventh and eighteenth terms.

Solution

To find a₁₁ , since 11 is odd, we put n = 11 in a_n = n(n + 3)

Thus, the eleventh term a₁₁ = 11(11 + 3) = 154 .

To finda₁₈ , since 18 is even, we put           n = 18 in a _n = n² + 1

Thus, the eighteenth term                           a₁₈ = 18 ² + 1 = 325.

Arithmetic Progression

Let us begin with the following two illustrations

Illustration 1

Make the following figures using match sticks

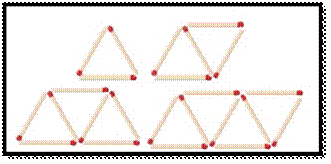
(i) How many match sticks are required for each figure? 3,5,7 and 9.

(ii) Can we find the difference between the successive numbers?

5 − 3 = 7 − 5 = 9 − 7 = 2

Therefore, the difference between successive numbers is always 2.

Illustration 2

A man got a job whose initial monthly salary is fixed at ₹10,000 with an annual increment of ₹2000. His salary during 1st , 2nd and 3rd years will be ₹ 10000, ₹ 12000 and ₹ 14000 respectively.

If we now calculate the difference of the salaries for the successive years, we get 12000 – 10000 = 2000; 14000 – 12000 = 2000 . Thus the difference between the successive numbers (salaries) is always 2000.

Did you observe the common property behind these two illustrations? In these two examples, the difference between successive terms always remains constant. Moreover, each term is obtained by adding a fixed number (2 and 2000 in illustrations 1 and 2 presented above) to the preceding term except the first term. This fixed number which is a constant for the differences between successive terms is called the “common difference”.

Example:

Check whether the following sequences are in A.P. or not?

 (i) x + 2,  2x + 3,  3x + 4,….

(ii) 2, 4, 8, 16,...

(iii) 3√2, 5√2, 7√2, 9√2,...

Solution

To check that the given sequence is in A.P., it is enough to check if the differences between the consecutive terms are equal or not.

(i) t ₂ -t₁ = (2x + 3) − (x + 2) = x + 1

t ₃ -t₂ = (3x + 4) − (2x + 3) = x + 1

t ₂ - t₁ = t ₃ − t₂

Thus, the differences between consecutive terms are equal.

Hence the sequence x + 2, 2x + 3, 3x + 4,... is in A.P.

(ii) t ₂ -t₁ = 4 − 2 = 2

t ₃ -t₂ = 8 − 4 = 4

t ₂ -t₁ = t ₃ −t₂

Thus, the differences between consecutive terms are not equal. Hence the terms of the sequence 2, 4, 8, 16, . . . are not in A.P.

(iii) t₂ -t₁  = 5√2 − 3√ 2 = 2√ 2

t₃ -t₂  = 7√2 − 5√ 2 = 2√ 2

t₄ -t₃  = 9√ 2 − 7√2 = 2√ 2

Thus, the differences between consecutive terms are equal. Hence the terms of the sequence 3√2, 5√2, 7√2, 9√2,... are in A.P

Example :

Write an A.P. whose first term is 20 and common difference is 8.

Solution

First term = a = 20 ; common difference = d= 8

Arithmetic Progression is a, a + d, a + 2d , a + 3d,...

In this case, we get 20, 20 + 8, 20 + 2(8),  20 + 3(8),...

So, the required A.P. is 20, 28, 36, 44,…..

Example :

Find the 15^th, 24^th and n^th term (general term) of an A.P. given by 3, 15, 27, 39,…….

Solution

We have, first term = a = 3 and common difference = d = 15 − 3 = 12 .

We know that n^{th  term} (general term) of an A.P. with first term a and common difference d is given by

t_n = a + (n −1)d

t₁₅ = a + (15 −1)d = a + 14d = 3 + 14 (12) = 171

(Here a = 3 and d = 12)

t₂₄= a + (24 −1)d = a + 23d = 3 +23(12) = 279

The n^th (general term) term is given by

t_n = a + (n − 1)d

Thus, t_n = 3 + (n −1)12

t_n = 12n − 9

Example:

Find the number of terms in the A.P. 3, 6, 9, 12,…, 111.

Solution

First term a = 3 ; common difference d = 6 − 3 = 3 ; last term l = 111

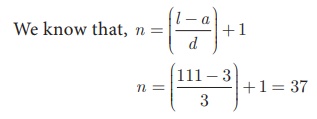
Thus the A.P. contain 37 terms.

Example :

Determine the general term of an A.P. whose 7^th term is −1 and 16^th term is 17.

Solution

Let the A.P. be t₁ , t ₂ ,t ₃ , t ₄,...

It is given that t₇ = −1 and t₁₆ = 17

a + (7 −1)d = −1 and a + (16 −1)d = 17

a + 6d = −1 ...(1)

a + 15d = 17 ...(2)

Subtracting equation (1) from equation (2), we get 9d = 18 gives d = 2

Putting d = 2 in equation (1), we get a + 12 = −1  so a = –13

Hence, general term t_n  = a + (n −1)d

= −13 + (n −1)×2 = 2n −15

Example :

If l^th , m^th and n^th terms of an A.P. are x, y, z respectively, then show that

(i) x (m − n ) + y (n − l ) + z (l − m) = 0 (ii) (x − y )n + (y − z )l + (z− x )m = 0

Solution

(i) Let a be the first term and d be the common difference. It is given that

t_l  = x, tm  = y, t_n  = z

Using the general term formula

a + (l −1)d = x ...(1)

a + (m −1)d = y ...(2)

a + (n −1)d = z ...(3)

We have, x (m − n ) + y(n − l ) + z (l −m)

=a [(m −n ) + (n − l ) + (l −m )] + d [(m −n)(l − 1) + (n − l )(m −1) + (l −m)(n −1)]

=a [0] +d[lm − ln −m + n + mn − lm −n + l +ln − mn −l + m]

=a(0) + d(0) = 0

(ii) On subtracting equation (2) from equation (1), equation (3) from equation (2) and equation (1) from equation (3), we get

x − y = (l −m)d

y− z = (m −n)d

z −x = (n −l)d

(x − y )n + (y − z )l + (z − x)m = [(l −m)n + (m −n )l + (n −l)m ]d = ln − mn + lm − nl + nm − lm d = 0

Example :

In an A.P., sum of four consecutive terms is 28 and their sum of their squares is 276. Find the four numbers.

Solution

Let us take the four terms in the form (a - 3d), (a -d), (a + d) and (a + 3d) .

Since sum of the four terms is 28,

a − 3d +a − d +a + d +a + 3d = 28

4a = 28 gives a = 7

Similarly, since sum of their squares is 276,

(a − 3d)²  + (a − d )²  + (a + d )²  + (a + 3d)² = 276.

a² − 6ad + 9d² + a² − 2ad + d² +a² + 2ad +d² + a² + 6ad + 9d²  = 276

4a²  + 20d²  =276 ⇒ 4(7)²  + 20d²  = 276. 

d²  = 4  gives d =  2

If d = 2 then the four numbers are 7 - 3(2),   7 – 2, 7 + 2, 7+3(2)

That is the four numbers are 1, 5, 9 and 13.

If a = 7, d = −2 then the four numbers are 13, 9, 5 and 1

Therefore, the four consecutive terms of the A.P. are 1, 5, 9 and 13.

Example:

A mother devides ₹207 into three parts such that the amount are in A.P. and gives it to her three children. The product of the two least amounts that the children had ₹4623. Find the amount received by each child.

Solution

Let the amount received by the three children be in the form of A.P. is given by

a –d , a, a + d . Since, sum of the amount is ₹207, we have

(a − d ) +a + (a +d) = 207

3a = 207 gives a = 69

It is given that product of the two least amounts is 4623.

(a − d )a = 4623

(69 − d )69 = 4623 

d = 2

Therefore, amount given by the mother to her three children are

₹(69−2), ₹69, ₹(69+2). That is, ₹67, ₹69 and ₹71.

SERIES

The sum of the terms of a sequence is called series. Leta₁, a₂, a₃,..., a_n ,... be the sequence of real numbers. Then the real number a₁ + a₂ + a₃ +… is defined as the series of real numbers.

If a series has finite number of terms then it is called a Finite series. If a series has infinite number of terms then it is called an Infinite series. Let us focus our attention only on studying finite series

SUM TO N TERMS OF AN A.P.

A series whose terms are in Arithmetic progression is called Arithmetic series.

Let a , a + d , a + 2d , a + 3d,... be the Arithmetic Progression.

The sum of first n terms of a Arithmetic Progression denoted by S_n is given by,

S_n=a +(a + d ) +(a + 2d ) +  + (a +(n −1)d )                 …….(1)

Rewriting the above in reverse order

S_n =(a +(n − 1)d) +(a + (n −2)d ) +  +(a + d ) +a         ..(2)

Adding (1) and (2) we get,

2S _n  =[a +a + (n −1)d ]+[ a +d +a +(n − 2)d ] + … + [a +(n − 2)d +(a +d )]+[a + (n −1)d +a]

= [2a +(n − 1)d ] +[2a + (n −1)d + .. .. +[2a + (n −1)d ]    (n terms)

2S_n= n ×[2a + (n −1)d ]      gives S_n  = n/2 [2a + (n − 1)d ]

Example:

Find the sum of first 15 terms of the A. P.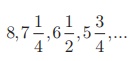

Solution

Here the first term a = 8, common difference d  =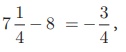

Sum of first n terms of an A.P. 

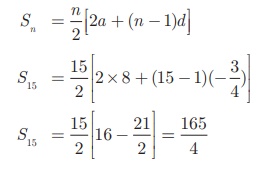
Example :

Find the sum of 0. 40 + 0. 43 + 0. 46 + + 1 .

Solution

Here the value of n is not given. But the last term is given. From this, we can find the value of n.

Given a = 0. 40 and l = 1 , we find d= 0. 43 − 0.40 = 0. 03 .

Therefore,

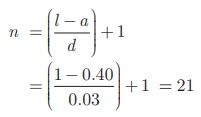
Sum of first n terms of an A.P. S_n = 

Here, n = 21 .  Therefore,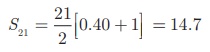 

So, the sum of 21 terms of the given series is 14.7.

Example :

How many terms of the series 1 + 5 + 9 + ... must be taken so that their sum is 190?

Solution

Here we have to find the value of n, such that S_n = 190.

First term a = 1, common difference d = 5 −1 = 4 .

Sum of first n terms of an A.P.

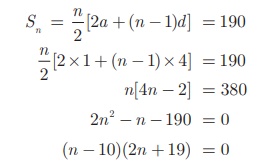
But n = 10 as n = −19/2 is impossible. Therefore, n = 10 .

Example:

The 13th term of an A.P. is 3 and the sum of first 13 terms is 234. Find the common difference and the sum of first 21 terms.

Solution

Given the 13^th term = 3 so, t₁₃ = a + 12d = 3             .........(1)

Sum of first 13 terms = 234  gives S ₁₃ =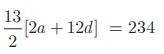 

2a + 12d = 36             .........(2)

Solving (1) and (2) we get, a = 33, d = −5 /2

Therefore, common difference is -5/2

Sum of first 21 terms = S₂₁

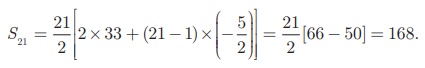
Example :

In an A.P. the sum of first n terms is 5n²/2 + 3n/2 . Find the 17^th term.

Solution 

The 17^th term can be obtained by subtracting the sum of first 16 terms from the sum of first 17 terms.

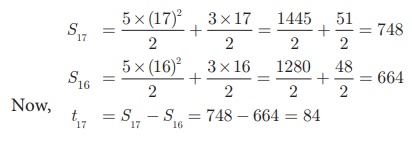
Example :

Find the sum of all natural numbers between 300 and 600 which are divisible by 7.

Solution

The natural numbers between 300 and 600 which are divisible by 7 are 301, 308, 315, …, 595.

The sum of all natural numbers between 300 and 600 is 301 + 308 + 315 + + 595.

The terms of the above series are in A.P.

First term a = 301 ; common difference d = 7 ; Last term l = 595.

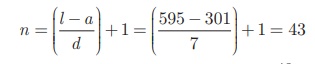
Since, S_n  = n/2 [a +l ] , we have S₅₇  = 43/2 [ 301 + 595]= 19264.

GEOMETRIC PROGRESSION

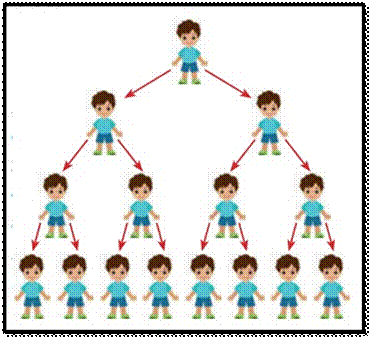
In the diagram given in Fig.2.13, ΔDEF is formed by joining the mid points of the sides AB, BC and CA of ΔABC. Then the size of the triangle ΔDEF is exactly one-fourth of the size of ΔABC. Similarly ΔGHI is also one-fourth of ΔFDE and so on. In general, the successive areas are one-fourth of the previous areas.

The area of these triangles are D ABC,

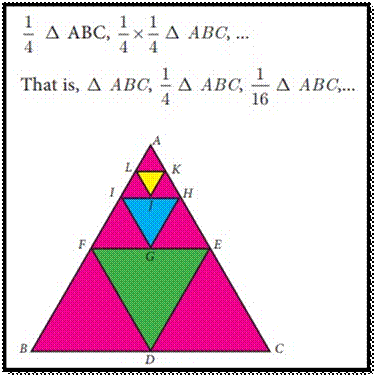
In this case, we see that beginning with ΔABC, we see that the successive triangles  are formed whose  areas are precisely one-fourth the area of the previous triangle. So, each term is obtained by multiplying 1/4 to the previous term.

1. GENERAL FORM OF GEOMETRIC PROGRESSION

Let a and r ≠ 0 be real numbers. Then the numbers of the form a , ar , ar² , ... ar^n-1... is called a Geometric Progression. The number ‘a’ is called the first term and number ‘r’ is called the common ratio.

We note that beginning with first term a, each term is obtained by multiplied with the common ratio ‘r’ to give ar , ar ² ,ar ³,...

2. GENERAL TERM OF GEOMETRIC PROGRESSION

We try to find a formula for n^th term or general term of Geometric Progression (G.P.) whose terms are in the common ratio.

a , ar , ar² ,..., ar^n-1, ... where a is the first term and ‘r’ is the common ratio. Let t_n be the n^th term of the G.P.

Then

t₁ = a = a × r⁰   = a ×r¹⁻¹

t₂ = t₁ × r = a × r = a × r²⁻¹

t₃ = t₂ × r = ar × r = ar² = ar³⁻¹

:            :

t_n = t_{n −1} × r = ar^{n −2} × r = ar^{n −2+1} = ar ⁿ⁻¹

Thus, the general term or n^th  term of a G.P. is t_n = ar^n-1

Example :

Which of the following sequences form a Geometric Progression?

(i) 7, 14, 21, 28, …

(ii) 1/ 2 , 1, 2, 4, ...

(ii) 5, 25, 50, 75, …

Solution

To check if a given sequence form a G.P. we have to see if the ratio between successive terms are equal.

(i) 7, 14, 21, 28, …

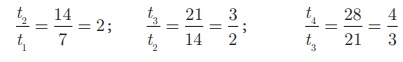
Since the ratios between successive terms are not equal, the sequence 7, 14, 21, 28, … is not a Geometric Progression.

(ii) 

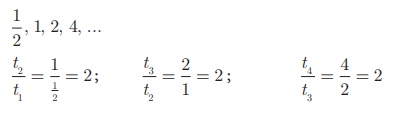
Here the ratios between successive terms are equal. Therefore the sequence 1/2 , 1, 2, 4, ... is a Geometric Progression with common ratio r= 2.

(iii) 5, 25, 50, 75,...

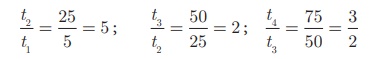
Since the ratios between successive terms are not equal , the sequence 5, 25, 50, 75,... is not a Geometric Progression.

Example :

Find the geometric progression whose first term and common ratios are given by

(i) a = −7 , r = 6

(ii) a = 256 , r = 0.5

Solution

(i) The general form of Geometric progression is a, ar, ar² ,.. .

 a = −7 , ar = −7 × 6 = −42 , ar ²  = −7 × 6²  = −252

(ii) The general form of Geometric progression is a, ar, ar² ,...

a = 256 , ar = 256 × 0.5 = 128 , ar ² = 256 ×(0.5)² = 64

Therefore the required Geometric progression is 256,128, 64,....

Example :

Find the 8^th term of the G.P. 9, 3, 1,…

Solution

To find the 8^th term we have to use the n^th term formula t_n = arⁿ⁻¹

First term a = 9 , common ratio r =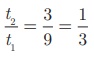 

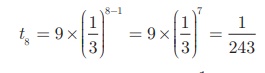
Therefore the 8^th term of the G.P. is 1/243

Example :

In a Geometric progression, the 4^th term is 8/9 and the 7^th term is 64/243. Find the Geometric Progression.

Solution

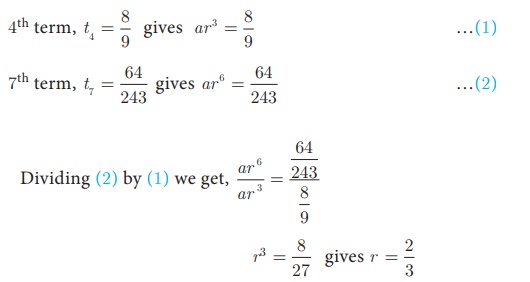
Substituting the value of r in (1), we get a × [2/3]³ = 8/9 ⇒ a = 3

Therefore the Geometric Progression is a, ar, ar² , … That is, 3, 2, 4/3,…..

SUM TO N TERMS OF A G.P :

A series whose terms are in Geometric progression is called Geometric series.

Let a, ar, ar² , ...ar^n-1 , ... be the Geometric Progression.

The sum of first n terms of the Geometric progression is

S_n = a +ar + ar ² +  + ar^{n −2} +arⁿ⁻¹                                                       ... (1)

Multiplying both sides by r, we get rS_n  = ar +ar² + ar³ +  + ar^n −1 +arⁿ … (2)

(2)−(1) gives rS_n − S _n  = arⁿ –a

S_n (r −1) = a(rⁿ –1)

Thus, the sum to n terms is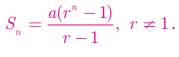

Find the sum of 8 terms of the G.P. 1, − 3, 9, −27…

Solutions

Here the first term a = 1 , common ratio r = -3/1 = -3 < 1, Here n = 8.

Sum to n terms of a G.P. is 

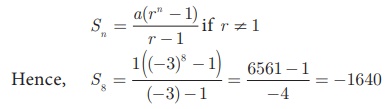
Find the first term of a G.P. in which S₆ = 4095 and r = 4.

Solution

Common ratio = 4 > 1 , Sum of first 6 terms S₆  = 4095 

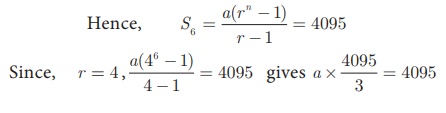
First term a = 3 .

How many terms of the series 1 + 4 + 16 + make the sum 1365 ?

Solution

Let n be the number of terms to be added to get the sum 1365

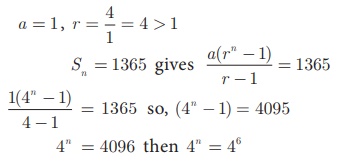
4ⁿ  = 4096 then 4ⁿ  = 4⁶

n = 6

Find the sum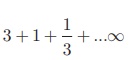 

Solution

Here a = 3 ,

Sum of infinite terms =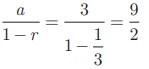 

Example 2.50 

Find the rational form of the number 0.6666¼

Solution

We can express the number 0.6666¼as follows

0.6666… = 0.6 + 0.06 + 0.006 + 0.0006 +

We now see that numbers 0.6, 0.06, 0.006 ... forms an G.P. whose first term a = 0.6

and common ration r = 0.06 / 0.6 = 0.1 . Also − 1 < r = 0.1 < 1

Using the infinite G.P. formula, we have

0.6666... = 0.6 + 0.06 + 0.006 + 0.0006 +  ...  = 

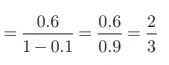
Thus the rational number equivalent of 0.6666 is 2/3

SPECIAL SERIES:

There are some series whose sum can be expressed by explicit formulae. Such series are called special series.

Here we study some common special series like

(i) Sum of first ‘n’ natural numbers

(ii) Sum of first ‘n’ odd natural numbers.

(iii) Sum of squares of first ‘n’ natural numbers.

(iv) Sum of cubes of first ‘n’ natural numbers.

We can derive the formula for sum of any powers of first n natural numbers using the expression (x + 1)^k +1 − x ^k +1 . That is to find 1^k + 2^k + 3^k + ... + n^k we can use the expression (x + 1)^{k +1} − x ^{k +1} .

1. Sum of first n natural numbers

To find1 + 2 + 3 + + n , let us consider the identity (x + 1)² − x ² = 2x + 1

When x = 1 , 2² − 1² = 2(1) + 1

When x = 2 , 3² − 2²  = 2(2) + 1

When x = 3 , 4² − 3²  = 2(3) + 1

                       :     :         :

When x = n −1 , n ² − (n −1)² = 2(n −1) + 1

When x = n −1 , (n + 1)²  - n ²= 2(n) + 1

Adding all these equations and cancelling the terms on the Left Hand side, we get,

(n + 1)² −1² = 2(1 + 2 + 3 +  + n ) + n

n ² + 2n= 2(1 + 2 + 3 +  + n ) + n

2(1 + 2 + 3 +  + n) = n ²  + n = n (n + 1)

1 + 2 + 3 +  + n= [n (n + 1)] / 2

2. Sum of first n odd natural numbers

1 + 3 + 5 + + (2n −1)

It is an A.P. with a = 1 , d = 2 and l = 2n −1

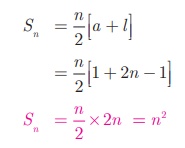
3. Sum of squares of first n natural numbers

To find1² + 2² + 3² + + n² , let us consider the identity (x + 1)³ − x ³  = 3x ²  + 3x + 1

When x = 1 , 2 ³ − 1³  = 3(1)²  + 3(1) + 1

When x = 2 , 3 ³ − 2 ³  = 3(2)²  + 3(2) + 1

When x = 3 , 4 ³ − 3 ³  = 3(3)² + 3(3) + 1

               :            :                     :

When x = n −1 , n ³ − (n −1)³ = 3(n −1)² + 3(n −1) + 1

When x = n , (n + 1)³ −n³ = 3n ² + 3n + 1

4. Sum of cubes of first n natural numbers

To find 1³ + 2³ + 3³ + + n³ , let us consider the identity 

(x + 1)⁴ − x ⁴  = 4x ³ + 6x ² + 4x + 1

When x = 1 , 2 ⁴ − 1⁴ = 4(1)² + 4(1) + 1

When x =2 , 3⁴ − 2 ⁴ = 4(2)³ + 4(2) + 1

When x = 3 , 4⁴ − 3 ⁴ = 4(3)³ + 6(3) + 1

               :                    :               :

When x = n −1 ,n⁴ − (n −1)⁴ = 4(n −1)³  + 4(n −1) + 1

When x = n , (n + 1)⁴ −n⁴  = 4n³ + 6n² + 4n + 1

Adding all these equations and cancelling the terms on the Left Hand side, we get,

(n+1)⁴–1⁴ = 4(1³ + 2^{3 +} 3 ³ +  + n ³ ) + 6(1² + 2² + 3² +  + n² ) + 4(1 + 2 + 3 +  + n ) + n

n⁴ + 4n³ + 6n² + 4n = 4(1³ + 2³ + 3 ³ +  + n ³ ) + 6 ×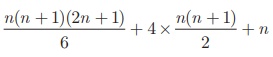 

4(1³ + 2³ + 3³ + … + n³ ) = n⁴    + 4n³ + 6n ² +4n − 2n³ −n² − 2n² − n − 2n² − 2n –n

4(1³ + 2³ + 3³ + … + n³ ) = n⁴    + 2n³ + n ² = n² (n² + 2n +1) = n²(n+1)²

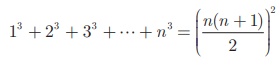
Example:

Find the value of (i) 1 + 2 + 3 + ... + 50 (ii) 16 + 17 + 18 + ... + 75

Solution

(i) 1+ 2 + 3 +  + 50

Using, 1 + 2 + 3 +  + n =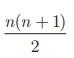 

 1+ 2 + 3 +  + 50  =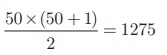 

(ii)  16 + 17 + 18 +  + 75  = (1 + 2 + 3 +  + 75) −(1 + 2 + 3 +  + 15) 

=75(75 + 1)/2 ₋ 15(15 + 1) / 2

=2850 −120 = 2730

Example :

Find the sum of

(i) 1 + 3 + 5 + … + to 40 terms

(ii) 2 + 4 + 6 + … + 80

(iii) 1+3 + 5 + … + 55

Solution

(i) 1+3 + 5 +… 40 terms = 40²  = 1600

(ii) 2 + 4 + 6 + … + 80 = 2(1 + 2 + 3 + … + 40) = 2 × [40 × (40 + 1)]/2 = 1640

(iii) 1 + 3 + 5 + …  + 55

Here the number of terms is not given. Now we have to find the number of terms using the formula, n = (l-a)/d + 1 gives n= [(55-1)/2] + 1 = 28

Therefore, 1 + 3 + 5 +  + 55 = (28)²  = 784

Example :

Find the sum of  

(i) 1² + 2² +  + 19²

(ii) 5² + 1 0² + 15² +  + 105² 

(iii) 15² + 16² + 17 ² +  + 28²

Solution

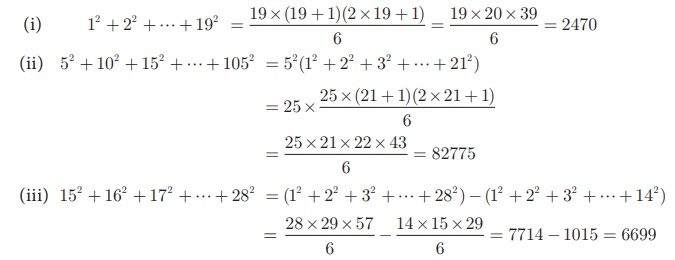
Example:

Find the sum of (i) 1³ + 2³ + 3³ +  + 16³ (ii) 9³ + 10³ +  + 21³

Solution