ALGEBRA
Differences between Simultaneous Linear Equations in Two Variables and
Simultaneous Linear Equations in Three Variables.
|
s.no |
Simultaneous Linear Equations in Two
Variables |
Simultaneous Linear Equations in Three
Variables |
|
1. |
Any first-degree equation containing two variables x
and y is called a linear equation in two variables. |
Any first-degree equation containing two variables
x, y and z is called a linear equation in three variables. |
|
2. |
The general form of linear equation in two variables
x and y is ax+by+c = 0, where at least one of a, b is non-zero and a, b, c
are real numbers. |
The general form of a linear equation in three
variables x, y and z is ax+by+cz +d = 0 where a, b, c, d are real numbers,
and at least one of a, b, c is non-zero. |
|
3. |
A linear equation in two variables of the form ax by
c ++ = 0, represents a straight line. |
A linear equation in three variables of the form ax
by cz d +++= 0, represents a plane. |
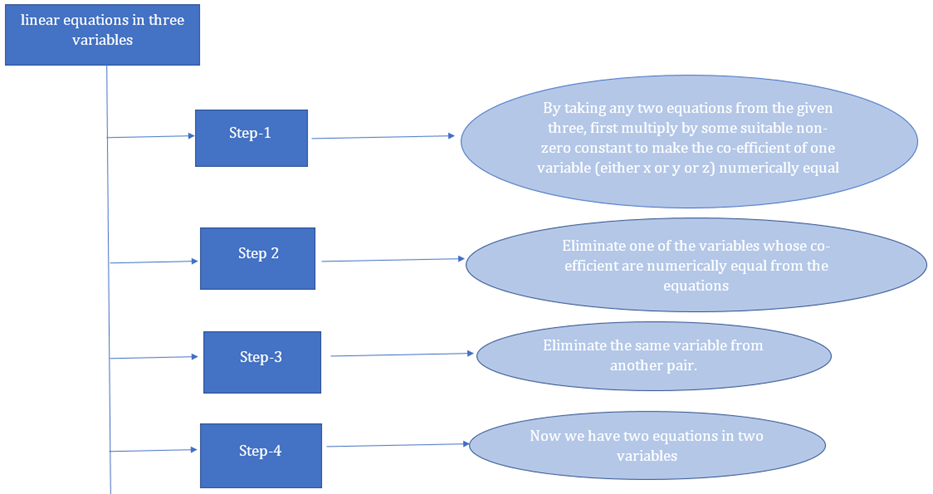
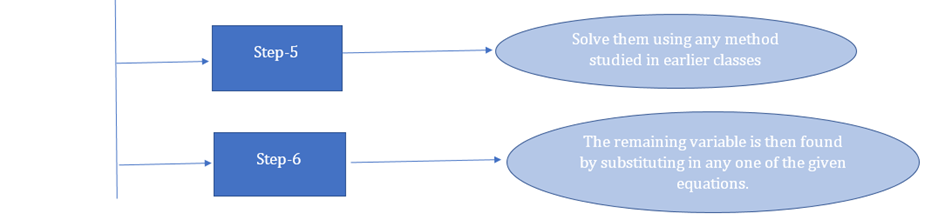
Procedure for solving system of linear equations in three variables
Rational Expressions
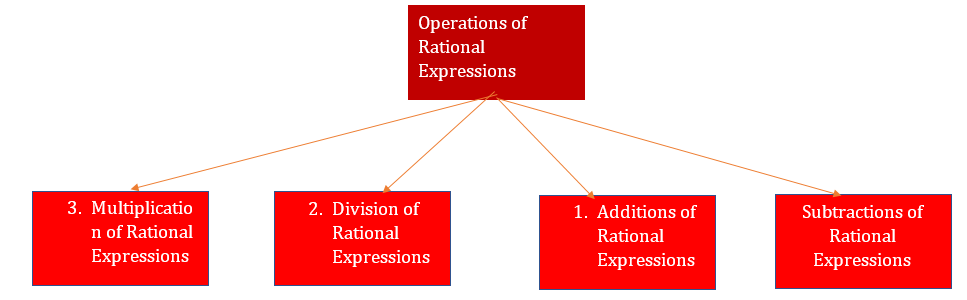
Operations of
Rational Expressions
1.
Multiplication of Rational Expressions
2.
Division of Rational Expressions
3.
Additions of Rational Expressions
4.
Subtractions of Rational Expressions
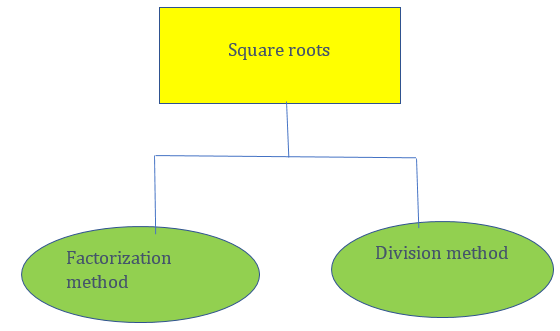
Square Root of
Polynomials
The following two methods are used to find the square root of
a given expression
(i)
Factorization method
(ii)
Division method
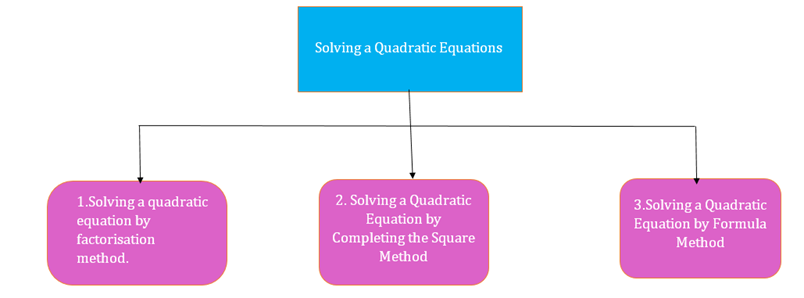
Quadratic Equations
Solving a Quadratic
Equations
1.
Solving a quadratic equation by factorisation
method.
2.
Solving a Quadratic Equation by Completing the
Square Method
3.
Solving a Quadratic Equation by Formula Method
Matrices
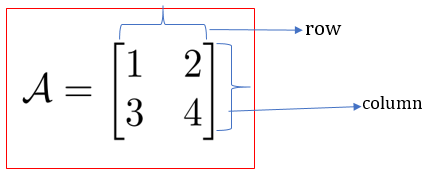
Matrix- A matrix is a rectangular
array of elements.
Rows- The horizontal arrangements are
called rows.
Columns- The vertical arrangements
are called columns.
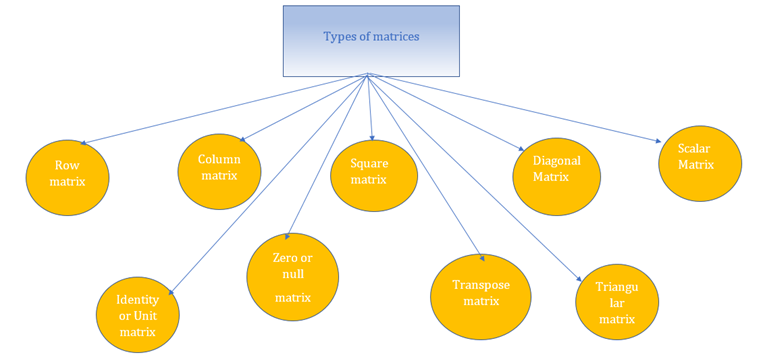
Types of Matrices
The following are the different types
of matrices
1.
Row Matrix
2.
Column Matrix
3.
Square Matrix
4.
Diagonal Matrix
5.
Scalar Matrix
6.
Identity (or) Unit Matrix
7.
Zero matrix (or) null matrix
8.
Transpose of a matrix
9. Triangular Matrix
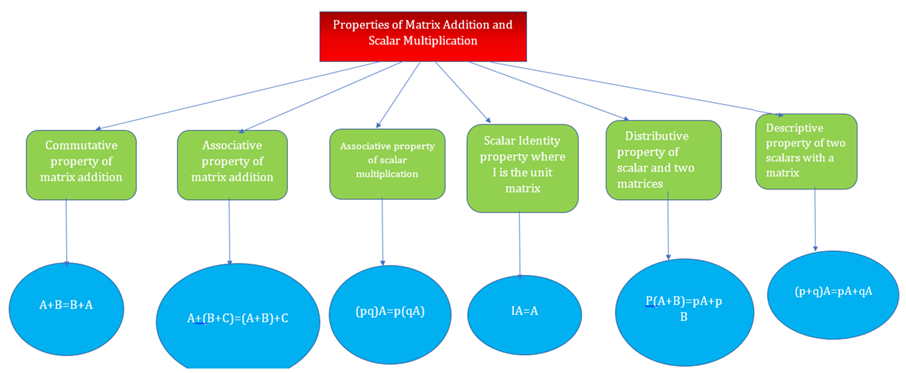
Properties of Matrix Addition and Scalar Multiplication