BASIC ALGEBRA

INTRODUCTION:

Algebra helps in solving the mathematical equations and to derive the unknown quantities, like the bank interest, proportions, percentages. The letter variables in the algebra can be used to represent the unknown quantities which are coupled with the ability to rewrite the equations making it easier in finding the data for a given set of equations.

The algebraic formulas are used in our daily life to find the distance, the volume of containers, and to figure out the sales prices as and when needed. Algebra is very helpful in stating a mathematical equation and relationship by making use of letters or other symbols representing as entities. The values of the equations of unknown quantities can be solved through algebra.

Some of the main topics coming under algebra include Basics of algebra, exponents, simplifying of algebraic expressions, polynomials, quadratic equations, etc.

Real Numbers:

Real numbers can be defined as the union of both the rational and irrational numbers. They can be both positive or negative and are denoted by the symbol “R”. All the natural numbers, decimals, and fractions come under this category.

Set of Real Numbers

The set of real numbers consist of different categories, such as natural and whole numbers, rational and irrational numbers and integers. In the table given here, all these numbers are defined with examples.

Category	Definition	Example
Natural Numbers	Contain all counting numbers which start from 1. N = {1,2,3,4,……}	All numbers such as 1, 2, 3, 4,5,6,…..…
Whole Numbers	Collection of zero and natural number. W = {0,1,2,3,…..}	All numbers including 0 such as 0, 1, 2, 3, 4,5,6,…..…
Integers	The collective result of whole numbers and negative of all natural numbers.	Includes: -infinity (-∞),……..-4, -3, -2, -1, 0, 1, 2, 3, 4, ……+infinity (+∞)
Rational Numbers	Numbers that can be written in the form of p/q, where q≠0.	Examples of rational numbers are ½, 5/4 and 12/6 etc.
Irrational Numbers	All the numbers which are not rational and cannot be written in the form of p/q.	Irrational numbers are non-terminating and non-repeating in nature like √2

Number Line:

A number line is a pictorial representation of numbers on a straight line. It’s a reference for comparing and ordering numbers. It can be used to represent any real number that includes every whole number and natural numbers. Just to recollect, the whole number is a set of numbers which include all counting numbers (1, 2, 3,4,5,6 …….) and zero (0), whereas the natural number is the set of all counting numbers i.e. 1, 2, 3, 4, 5, 6……..

Numbers on a Number Line

Arithmetic operations of numbers can be better explained on a number line. To begin with, one must know to locate numbers on a number line. Zero is the middle point of a number line. All (natural numbers) positive numbers occupy the right side of the zero whereas negative numbers occupy the left side of zero on the number line. As we move on to the left side value of a number decreases. For example, 1 is greater than -2. In a number line, integers, fractions, and decimals can also be represented easily.

Irrational Numbers:

An irrational number is a real number that cannot be expressed as a ratio of integers, for example, √ 2 is an irrational number. Again, the decimal expansion of an irrational number is neither terminating nor recurring. How do you know a number is irrational? The real numbers which cannot be expressed in the form of p/q, where p and q are integers and q ≠ 0 are known as irrational numbers. For Example  √ 2 and √ 3 etc. Whereas any number which can be represented in the form of p/q, such that, p and q are integers and q ≠ 0 is known as a rational number

Example:

Which of the following are Rational Numbers or Irrational Numbers?

2, -.45678…, 6.5, √ 3, √ 2

Solution:

Rational Numbers – 2, 6.5 as these are terminating numbers.

Irrational Numbers – -.45678…, √ 3, √ 2 as these are non-terminating numbers.

PROPERTIES OF REAL NUMBERS

There are four main properties which include commutative property, associative property, distributive property, and identity property. Consider “m, n and r” are the real numbers. Then based on these properties, we can define the numbers as;

COMMUTATIVE PROPERTY

If m and n are the numbers, then the general form will be m + n = n + m for addition and m.n = n.m for multiplication.

Addition: m + n = n + m. For example, 5 + 3 = 3 + 5, 2 + 4 = 4 + 2

Multiplication: m × n = n × m. For example, 5 × 3 = 3 × 5, 2 × 4 = 4 × 2

ASSOCIATIVE PROPERTY

If m, n and r are the numbers. The general form will be m + (n + r) = (m + n) + r for addition(mn) r = m (nr) for multiplication.

Addition: The general form will be m + (n + r) = (m + n) + r. An example of additive associative property is 10 + (3 + 2) = (10 + 3) + 2.

Multiplication: (mn) r = m (nr). An example of a multiplicative associative property is (2 × 3) 4 = 2 (3 × 4).

Distributive Property

For three numbers m, n, and r, which are real in nature, the distributive property is in the form of :

m (n + r) = mn + mr and (m + n) r = mr + nr.

Example of distributive property is: 5(2 + 3) = 5 × 2 + 5 × 3. Here, both sides will yield 25.

Identity Property

There are additive and multiplicative identities.

• For addition: m + 0 = m. (zero is additive identity)
• For multiplication: a × 1 = 1 × a = a. (1 is multiplicative identity).

ABSOLUTE VALUE:

The Value Which Refers to the distance of a number from the origin of a number line is called absolute values. It is represented as |a|, which defines the magnitude of any integer ‘a’. The absolute value of any integer, whether positive or negative, will be the real numbers, regardless of which sign it has.  It is represented by two vertical lines |a|, which are known as the modulus of a.

For Example: 5 is the absolute value for both 5 and -5.

|-5| = +5 and |+ 5| = +5

It helps in connecting the absolute value of complex numbers and the magnitudes of the vector.

We can define the absolute values like the following

{ a if a ≥ 0 }

|a| = { -a if a < 0 }

ABSOLUTE VALUE PROPERTIES

If x and y are real numbers and then the absolute values are satisfying the following properties,

Non-negativity

Positive-definiteness

Multiplicativeness:

Subadditivity:

Symmetry

Identity of indiscernible (equivalent to positive-definiteness)

Triangle inequality Triangle inequality (equivalent to subadditivity )

Preservation of division (equivalent to multiplicatively)

Equivalent to subadditivity

1.Non-negativity :

| x | ≥ 0

2.POSITIVE-DEFINITENESS:

| x | = 0 ↔ a = 0

3. MULTIPLICATIVENESS:

| x × y| = |x| × |y|

4. SUBADDITIVITY:

| x + y| ≤ | x | + | y |

5. SYMMETRY :

| – x | = | x |

6.IDENTITY OF INDISCERNIBLE (EQUIVALENT TO POSITIVE-DEFINITENESS) :

| x – y | = 0 ↔ a = b

7. TRIANGLE INEQUALITY TRIANGLE INEQUALITY (EQUIVALENT TO SUBADDITIVITY ) :

| x – y | ≤ | x – z | + | z – x |

8.PRESERVATION OF DIVISION (EQUIVALENT TO MULTIPLICATIVENESS) :

| x / y| = | x | / | y |

9. EQUIVALENT TO SUBADDITIVITY :

| x – y | ≥ | | x | – | y | |

LINEAR INEQUALITIES:

1. Solve 24x < 100, when

(i) x is a natural number.

(ii) x is an integer.

Solution:

(i) Given that 24x < 100

Now we have to divide the inequality by 24 then we get x < 25/6

Now when x is a natural integer then

It is clear that the only natural number less than 25/6 are 1, 2, 3, 4.

Thus, 1, 2, 3, 4 will be the solution of the given inequality when x is a natural number.

Hence {1, 2, 3, 4} is the solution set.

(ii) Given that 24x < 100

Now we have to divide the inequality by 24 then we get x < 25/6

now when x is an integer then

It is clear that the integer number less than 25/6 are…-1, 0, 1, 2, 3, 4.

Thus, solution of 24 x < 100 are…,-1, 0, 1, 2, 3, 4, when x is an integer.

Hence {…, -1, 0, 1, 2, 3, 4} is the solution set.

2. Solve – 12x > 30, when

(i) x is a natural number.

(ii) x is an integer.

Solution:

(i) Given that, – 12x > 30

Now by dividing the inequality by -12 on both sides we get, x < -5/2

When x is a natural integer then

It is clear that there is no natural number less than -2/5 because -5/2 is a negative number and natural numbers are positive numbers.

Therefore there would be no solution of the given inequality when x is a natural number.

(ii) Given that, – 12x > 30

Now by dividing the inequality by -12 on both sides we get, x < -5/2

When x is an integer then

It is clear that the integer number less than -5/2 are…, -5, -4, – 3

Thus, solution of – 12x > 30 is …,-5, -4, -3, when x is an integer.

Therefore the solution set is {…, -5, -4, -3}

3. Solve 5x – 3 < 7, when

(i) x is an integer

(ii) x is a real number

Solution:

(i) Given that, 5x – 3 < 7

Now by adding 3 both side we get,

5x – 3 + 3 < 7 + 3

Above inequality becomes

5x < 10

Again by dividing both sides by 5 we get,

5x/5 < 10/5

x < 2

When x is an integer then

It is clear that that the integer number less than 2 are…, -2, -1, 0, 1.

Thus, solution of 5x – 3 < 7 is …,-2, -1, 0, 1, when x is an integer.

Therefore the solution set is {…, -2, -1, 0, 1}

(ii) Given that, 5x – 3 < 7

Now by adding 3 both side we get,

5x – 3 + 3 < 7 + 3

Above inequality becomes

5x < 10

Again by dividing both sides by 5 we get,

5x/5 < 10/5

x < 2

When x is a real number then

It is clear that the solutions of 5x – 3 < 7 will be given by x < 2 which states that all the real numbers that are less than 2.

Hence the solution set is x ∈ (-∞, 2)

4. Solve 3x + 8 >2, when

(i) x is an integer.

(ii) x is a real number.

Solution:

(i) Given that, 3x + 8 > 2

Now by subtracting 8 from both sides we get,

3x + 8 – 8 > 2 – 8

The above inequality becomes,

3x > – 6

Again by dividing both sides by 3 we get,

3x/3 > -6/3

Hence x > -2

When x is an integer then

It is clear that the integer number greater than -2 are -1, 0, 1, 2,…

Thus, solution of 3x + 8 > 2is -1, 0, 1, 2,… when x is an integer.

Hence the solution set is {-1, 0, 1, 2,…}

(ii) Given that, 3x + 8 > 2

Now by subtracting 8 from both sides we get,

3x + 8 – 8 > 2 – 8

The above inequality becomes,

3x > – 6

Again by dividing both sides by 3 we get,

3x/3 > -6/3

Hence x > -2

When x is a real number.

It is clear that the solutions of 3x + 8 >2 will be given by x > -2 which states that all the real numbers that are greater than -2.

Therefore the solution set is x ∈ (-2, ∞).

QUADRATIC EQUATIONS:

Consider the quadratic equation: px²+qx+r=0 with real coefficients p, q, r and p≠0. Now, let us assume that the discriminant d < 0 i.e. b²−4ac<0. The solution of above quadratic equation will be in the form of complex numbers given by, x=−b±b²−4ac√2a = −b±i4ac−b²√2a

 Examples

1. Find the roots of equation x2+2=0

Solution: 

Give, x²+2=0

i.e. x²=−2 or x = ±2–√i

2. Solve x²+x+1=0

Solution: 

Given x²+x+1=0

Therefore, discriminant D = b²−4ac=1−4=−3

Therefore, the solution of given quadratic equation = −1±−3√2=−1±3i2

Quadratic Formula:

The roots of the quadratic equation: x = (-b ± √D)/2a, where D = b² – 4ac

2. Nature of roots:

D > 0, roots are real and distinct (unequal)

D = 0, roots are real and equal (coincident)

D < 0, roots are imaginary and unequal

3. The roots (α + iβ), (α – iβ) are the conjugate pair of each other.

4. Sum and Product of roots: If α and β are the roots of a quadratic equation, then

S = α+β= -b/a = coefficient of x/coefficient of x²

P = αβ = c/a = constant term/coefficient of x²

5. Quadratic equation in the form of roots: x² – (α+β)x + (αβ) = 0

6. The quadratic equations a₁x₂ + b₁x + c₁ = 0 and a₂x₂ + b₂x + c₂ = 0 have;

One common root if (b₁c₂ – b₂c₁)/(c₁a₂ – c₂a₁) = (c₁a₂ – c₂a₁)/(a₁b₂ – a₂b₁)

Both roots common if a₁/a₂ = b₁/b₂ = c₁/c₂

7. In quadratic equation ax² + bx + c = 0 or [(x + b/2a)² – D/4a²]

If a > 0, minimum value = 4ac – b²/4a at x = -b/2a.

If a < 0, maximum value 4ac – b²/4a at x= -b/2a.

8. If α, β, γ are roots of cubic equation ax³ + bx² + cx + d = 0, then, α + β + γ = -b/a, αβ + βγ + λα = c/a, and αβγ = -d/a

9. A quadratic equation becomes an identity (a, b, c = 0) if the equation is satisfied by more than two numbers i.e. having more than two roots or solutions either real or complex.

QUADRATIC INEQUALITIES:

Steps to Solve Quadratic Inequalities:

First solve ax2 + bx + c = 0.

If there are no real solutions, then one of the above inequality holds for all x ∈ R

If there are real solutions, which are called critical points, then label those points on the number line.

Note that these critical points divide the number line into disjoint intervals. (It is possible that there may be only one critical point.)

Choose one representative number from each interval.

Substitute that these representative numbers in the inequality.

(vii) Identify the intervals where the inequality is satisfied.

POLYNOMIAL FUNCTION:

A polynomial function is a function that can be expressed in the form of a polynomial. The definition can be derived from the definition of a polynomial equation. A polynomial is generally represented as P(x). The highest power of the variable of P(x)is known as its degree. Degree of a polynomial function is very important as it tells us about the behaviour of the function P(x) when x becomes very large. The domain of a polynomial function is entire real numbers (R).

If P(x) = a_n xⁿ + a_n-1 x^n-1+.……….…+a₂ x² + a₁ x + a₀, then for x ≫ 0 or x ≪ 0, P(x) ≈ a_n xⁿ. Thus, polynomial functions approach power functions for very large values of their variables.

Example:

A polynomial function has only positive integers as exponents. We can even perform different types of arithmetic operations for such functions like addition, subtraction, multiplication and division.

Some of the examples of polynomial functions are here:

x²+2x+1 = 0

3x-7=2

7x³+x²-2=0

All three expression above are polynomial since all of the variables have positive integer exponents. But expressions like;

5x^-1+1=0

4x^1/2+3x+1

(9x +1) ÷ (x)

are not polynomial equations, we cannot consider negative integer exponents or fraction exponent or division here.

Division Algorithm:

Given two polynomials f(x) and g(x), where g(x) is not the zero polynomial, there exist two polynomials q(x) and r(x) such that f(x) = q(x)g(x)+r(x) where degree of r(x) < degree of g(x).

Here, q(x) is called the quotient polynomial, and r(x) is called the remainder polynomial. If r(x) is the zero polynomial, then q(x), g(x) are factors of f(x) and f(x) = q(x)g(x). These terminologies are similar to terminologies used in division done with integers. If g(x) = x−a, then the remainder r(x) should have degree zero and hence r(x) is a constant. Todetermine the constant, write f(x) = (x − a)q(x) + c. Substituting x = a we get c = f(a).

RATIONAL FUNCTION:

A number that can be expressed in the form of pq where p and q are integers and q ≠ 0 , is a rational number.

A rational function R(x) is the function in the formP(x)Q(x)  where P(x) and Q(x) are polynomial functions and Q(x) is a non-zero polynomial.

R(x) = P(x)Q(x) ,Q(x) ≠ 0

From the given condition for Q(x),we can conclude that zeroes of the polynomial function in the denominator do not fall in the domain of the function. When Q(x) = 1,

i.e. a constant polynomial function, the rational function becomes a polynomial function.

PARTIAL FRACTIONS

Partial function: n algebraic fraction can be broken down into simpler parts known as “partial fractions“. Consider an algebraic fraction, (3x+5)/(2x²-5x-3). This expression can be split into simple form like ((2)/(x-3))-((1)/(2x+1))

The Simpler parts ((2)/(x-3))-((1)/(2x+1)) are known as partial fractions.

This means that an algebraic expression can be written in the form of

(3x+5)/(2x²-5x-3) = ((2)/(x-3))-((1)/(2x+1))

Partial Fractions From Rational Functions

Any number which can be easily represented in the form of p/q, such that p and q are integers and q≠0 are known as Rational numbers. Similarly, we can define a rational function as the ratio of two polynomial functions P(x) and Q(x), where P and Q are polynomials in x and Q(x)≠0. A rational function is known as proper if the degree of P(x) is less than the degree of Q(x) otherwise it is known as an improper rational function. With the help of the long division process, we can reduce improper rational functions to proper rational functions. Therefore, if P(x)/Q(x) is improper then it can be expressed as:

P(x)Q(x)=A(x)+R(x)Q(x)

Here, A(x) is a polynomial in x and R(x)/Q(x) is a proper rational function.

We know that the integration of a function f(x) is given by F(x) and it is represented by:

∫f(x)dx = F(x) + C

Here R.H.S. of the equation means integral of f(x) with respect to x.

Partial Fractions Decomposition

S.No	Rational Function	Partial Function
1	p(x)+q(x−a)(x−b)	Ax−a+B(x−b)
2	p(x)+q(x−a)^2	A1x−a+A2(x−a)^2
3	px^2+qx+r(x−a)(x−b)(x−c)	Ax−a+B(x−b)+C(x−c)
4	px^2+q(x)+r(x−a)2(x−b)	A1x−a+A2(x−a)^2+B(x−b)
5	px^2+qx+r(x−a)(x^2+bx+c)	Ax−a+Bx+Cx^2+bx+c

Example

Integrate the function 1(x−3)(x+1) with respect to x.

Solution:

The given integrand can be expressed in the form of partial fraction as:

1(x−3)(x+1)=A(x−3)+B(x+1)

To determine the value of real coefficients A and B, the above equation is rewritten as:

1= A(x+1)+B(x-3)

⇒1=x(A+B)+A-3B

Equating the coefficients of x and the constant, we have

A + B = 0

A – 3B = 1

Solving these equations simultaneously, the value of A =1/4 and B = -1/4. Substituting these values in the equation 1, we have

1(x−3)(x+1)=14(x−3)+−14(x+1)

Integrating with respect to x we have;

∫1(x−3)(x+1)=∫14(x−3)+∫−14(x+1)

According to the properties of integration, the integral of sum of two functions is equal to the sum of integrals of the given functions, i.e.,

∫[f(x) +g(x)]dx = ∫f(x)dx + ∫g(x)dx

Therefore,

=14∫1(x−3)–14∫1(x+1)

=14ln|x−3|–14ln|x+1|

=14ln∣∣x−3x+1∣∣

GRAPHICAL REPRESENTATION OF LINEAR INEQUALITIES:

An equation is a mathematical expression which involves “=” symbol. The right-hand side of the expression is equal to the left-hand side of the expression.

The statements involving symbols like ‘<’(less than), ‘>’ (greater than), ‘≤’’(less than or equal to), ‘≥’ (greater than or equal to) are called inequalities.

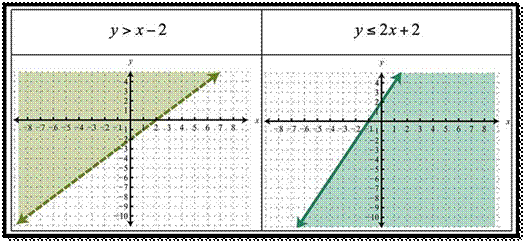
Example:

Following example validates the difference between equation and inequality:

Statement 1:

The distance between your house and school is exactly 4.5 kilometres,

The mathematical expression of the above statement is,

x = 4.5 km, where ‘x’ is the distance between house and the school.

Statement 2: The distance between your house and the school is at least 4.5 kilometers.

Here, the distance can be 4.5 km or more than that. Therefore the mathematical expression for the above statement is,

x ≥ 4.5 km, where ‘x’ is a variable which is equal to the distance between house and the school.

EXPONENTS:

Exponents are used to showing repeated multiplication of a number by itself. Writing large numbers sometimes becomes tedious. In large mathematical expressions, they occupy more space and take more time. This issue is resolved by the use of exponents. For example, 7 × 7 × 7 can be represented as 73. In this example, the exponent is ‘3’ which stands for the number of times the value is multiplied by itself. The number 7 is called the base which is the actual number that is getting multiplied. For instance, the speed of light is 300000000 m/s. This can be simply written as 3 × 108 m/s (approximate value). This process ofusing exponents is called as ‘raising to a power’ where the exponent is the power

Exponential Function:

An exponential function is a Mathematical function in form f (x) = a^x , where “x” is a variable and “a” is a constant which is called the base of the function and it should be greater than 0. The most commonly used exponential function base is the transcendental number e, which is approximately equal to 2.71828.

Exponential Function Formula

An exponential function is defined by the formula f(x) = a^x, where the input variable x occurs as an exponent. The exponential curve depends on the exponential function and it depends on the value of the x.

The exponential function is an important mathematical function which is of the form

f(x) = a^x

Where a>0 and a is not equal to 1.

x is any real number.

If the variable is negative, the function is undefined for -1 < x < 1.

Here,

“x” is a variable

“a” is a constant, which is the base of the function.

But, mostly the base of the exponential function is encountered by the transcendental number “e”, which is approximately equal to 2.71828.

Exponential Function Graph

The following figure represents the graph of exponents of x. It can be seen that as the exponent increases, the curves get steeper and the rate of growth increases respectively. Thus for x > 1, the value of y = f_n(x) increases for increasing values of (n).

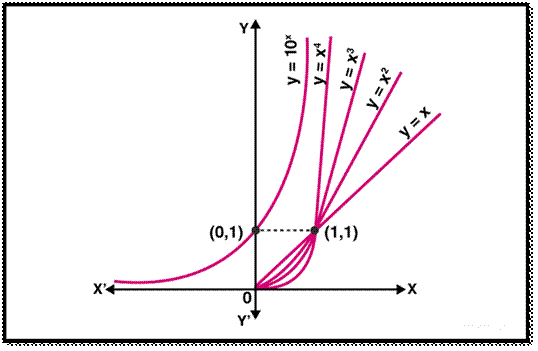
From the above discussion, it can be seen that the nature of polynomial functions is dependent on its degree. Higher the degree of any polynomial function, then higher is its growth. A function which grows faster than a polynomial function is y = f(x) = a^x, where a>1. Thus, for any of the positive integers n the function f (x) is said to grow faster than that of f_n(x).

Thus, the exponential function having base greater than 1, i.e., a > 1 is defined as y = f(x) = a^x. The domain of exponential function will be the set of entire real numbers R and the range are said to be the set of all the positive real numbers.

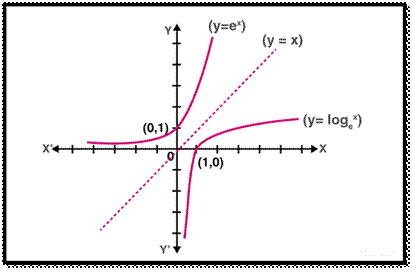
It must be noted that exponential function is increasing and the point (0, 1) always lies on the graph of an exponential function. Also, it is very close to zero if the value of x is largely negative.

Exponential function having base 10 is known as a common exponential function. Consider the following series:

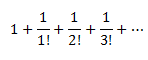
The value of this series lies between 2 &3. it is represented by e. Keeping e as base the function, we get y = e^x, which is a very important function in mathematics known as a natural exponential function.

For a > 1, the logarithm of b to base a is x if a^x = b. Thus, log_a b = x if a^x = b. This function is known as logarithmic function.

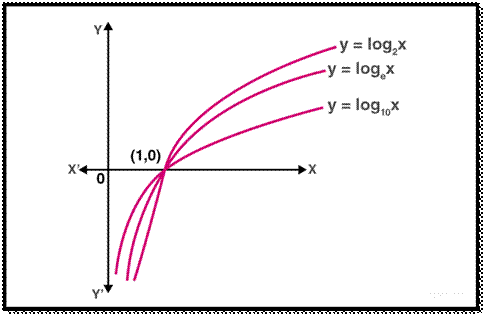
For base a = 10, this function is known as common logarithm and for the base a = e, it is known as natural logarithm denoted by ln x. Following are some of the important observations regarding logarithmic functions which have base a>1.

The domain of log function consists of positive real numbers only, as we cannot interpret the meaning of log functions for negative values.

For the log function, though the domain is only the set of positive real numbers, the range is set of all real values, I.e. R

When we plot the graph of log functions and move from left to right, the functions show increasing behaviour.

The graph of log function never cuts x-axis or y-axis, though it seems to tend towards them.

Log_ap = α, log_bp = β and log_ba = µ, then a^α = p, b^β = p and b^µ = a

Log_bpq = Log_bp + Log_bq

Log_bp^y = ylog_bp

Log_b (p/q) = log_bp – log_bq

LOGARITHM:

A logarithm is defined as the power to which number must be raised to get some other values. It is the most convenient way to express large numbers. A logarithm has various important properties that prove multiplication and division of logarithms can also be written in the form of logarithm of addition and subtraction.

“The logarithm of a positive real number a with respect to base b, a positive real number not equal to 1^{[nb 1]}, is the exponent by which b must be raised to yield a”.

i.e b^y= a and it is read as “the logarithm of a to base b.”

Logarithm Properties:

There are four basic rules of logarithms as given below:-

Log_b (mn)= log_b m + log_b n. In this rule, the multiplication of two logarithmic values is equal to the addition of their individual logarithms.

For example- log₃ ( 2y ) = log₃ (2) + log₃ (y)

Log_b (m/n)= log_b m – log_b This is called as division rule. Here the division of two logarithmic values is equal to the difference of each logarithm.

For example, log₃ ( 2/ y ) = log₃ (2) -log₃ (y)

Log_b (mⁿ) = n log_b ^m

         This is the exponential rule of logarithms. The logarithm of m with a rational exponent is equal to the exponent times its logarithm.

Log_b m = log_a m/ log_a b    

Logarithms Examples:

Solve log ₂ (64) =?

Solution:

since 2⁶= 2 × 2 × 2 × 2 × 2 × 2 = 64, 6 is the exponent value and log ₂ (64)= 6.

What is the value of log₁₀(100)?

Solution:

In this case, 10 ² yields you 100. So, 2 is the exponent value, and the value of log₁₀(100)= 2

Use of the property of logarithms, solve for the value of x for log₃ x= log₃ 4+ log₃ 7

Solution:

By the addition rule, log₃ 4+ log₃ 7= log ₃ (4 * 7 )

Log ₃ ( 28 ). Thus, x= 28.

Solve for x in log ₂ x = 5

Solution:

This logarithmic function can be written In the exponential form as 2 ⁵ = x

Therefore, 2 ⁵= 2 × 2 × 2 × 2 × 2 = 32, X= 32.

APPLICATION OF ALGEBRA IN REAL LIFE:

Algebra is used in many aspects of life. Financial planning is an area in daily life where algebra is used. Algebra concepts are used to calculate interest rates by bankers and as well as for calculating loan repayments. They are used to predict growth of money. Physical fitness is another area where calculations are made to determine the right amount of food intake for an individual taking into consideration such as the height, body mass of the person etc. Doctors use algebra in measuring drug dosage depending on age and weight of an individual. Architects depend on algebra to design buildings while civil engineers use it to design roads, bridges and tunnels. Algebra is needed to convert items to scale so that the structures designed have the correct proportions. It is used to programme computers and phones . Let us see some examples. Because of the extra-ordinary range of sensitivity of the human ear (a range of over 1000 million millions to one), it is useful to use logarithmic scale to measure sound intensity over this range. The unit of measure decibel is named after the inventor of the telephone Alexander Graham Bell. If we know the population in the world today, the growth, which is rapid, can be measured by approximating to an exponential function. The radioactive carbon-14 is an organism which decays according to an exponential formula.