TRIGONOMETRY

INTRODUCTION

Trigonometry is one of the major topics in Maths subject. Trigonometry deals with the measurement of angles and sides of a triangle. Usually, trigonometry logics are considered for the right-angled triangle. Also, its functions are used to find out the length of the arc of a circle, which forms a section in the circle with radius and its center point.

If we break the word trigonometry, ‘Tri’ is a Greek word which means ‘Three’, ‘Gon’ means ‘length’ and ‘metry’ means ‘measurement’. So basically, trigonometry is a study of triangles, which has angles and lengths on its side. Trigonometry basics consist of sine, cosine and tangent functions. T

ANGLE:

The amount of rotation about the point of intersection of two planes (or lines) which is required to bring one in correspondence with the other is called an Angle. There are many different types of angles which we will study in this article.

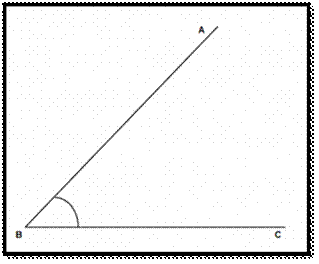
Angle :

In the angle ∠ABC(Like given above), it is generally represented by Greek letters such as θ, α, β etc.

It can also be represented by three letters of the shape that define the angle, with the middle letter being where the angle actually is (i.e.its vertex).

Eg. ∠ABC, where B is the given angle.

Angle measurement terms are – degree °, radians or gradians.

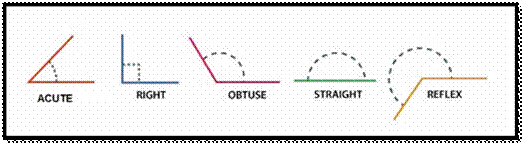
Types of Angles

Acute Angle – 0° to 90°, both exclusive.

Obtuse Angle – 90° to 180°, both exclusive.

Right Angle – Exactly 90°.

Straight Angle – Exactly 180°.

Reflex Angle – 180° to 360°, both exclusive.

Full Rotation – Exactly 360°

Different Systems of measurement of angle:

Sexagesimal System / Degree Measure

This is also called an English system.

In this system,

1^st right angle = 90^o

1^o = 60’

1’ = 60’’

Centesimal system of Angle Measurement

This is also known as French system.

{1}’ = {100}’\\ {1}’ = {100}”1’=100’1’=100”.

Circular system of Angle Measurement

This is very popularly known as radian system.

In this system, the angle is measured in radian

• A radian is an angle subtended at the centres of a circle by an arc, the whole length is equal to the radius of the circle.

Degree Measure:

The degree is a unit of measurement of angles and is represented by the symbol ◦. In degrees, we split up one complete rotation into 360 equal parts and each part is one degree, denoted by 1◦. Thus, 1◦ is 1/360 of one complete rotation. To measure a fraction of an angle and also for accuracy of measurement of angles, minutes and seconds are introduced. One minute (1 ) corresponds to 1/60 of a degree and in turn a second (1) corresponds to 1/60 of a minute (or) 1/3600 of a degree. We shall classify a pair of angles in the following way for better understanding and usages.

Two angles that have the exact same measure are called congruent angles.

Two angles that have their measures adding to 90◦ are called complementary angles.

Two angles that have their measures adding to 180◦ are called supplementary angles.

Two angles between 0◦ and 360◦ are conjugate if their sum equals 360◦.

Angles in Standard Position:

An angle is said to be in standard position if its vertex is at the origin and its initial side is along the positive x-axis. An angle is said to be in the first quadrant, if in the standard position, its terminal side falls in the first quadrant. Similarly, we can define for the other three quadrants. Angles in standard position having their terminal sides along the x-axis or y-axis are called quadrantal angles. Thus, 0◦, 90◦, 180◦, 270◦ and 360◦ are quadrantal angles. The degree measurement of a quadrantal angle is a multiple of 90◦.An angle is said to be in standard position if its vertex is at the origin and its initial side is along the positive x-axis. An angle is said to be in the first quadrant, if in the standard position, its terminal side falls in the first quadrant. Similarly, we can define for the other three quadrants. Angles in standard position having their terminal sides along the x-axis or y-axis are called quadrantal angles. Thus, 0◦, 90◦, 180◦, 270◦ and 360◦ are quadrantal angles. The degree measurement of a quadrantal angle is a multiple of 90◦.

Conterminal angles:

Conterminal angles 45° 405° -315° x y Initial Side Figure 3.3 One complete rotation of a ray in the anticlockwise direction results in an angle measuring of 360◦. By continuing the anticlockwise rotation, angles larger than 360◦ can be produced. If we rotate in clockwise direction, negative angles are produced. Angles 57◦, 417◦ and −303◦ have the same initial side and terminal side but with different amount of rotations, such angles are called coterminal angles. Thus, angles in standard position that have the same terminal sides are coterminal angles . Hence, if α and β are coterminal angles, then β = α + k(360◦), k is an integer. The measurements of coterminal angles differ by an integral multiple of 360◦. For example, 417◦ and −303◦ are coterminal because 417◦ − (−303◦) = 720◦ = 2 (360◦).

Basic Trigonometric ratios using a right triangle:

It is defined as the values of all the trigonometric function based on the value of the ratio of sides in a right-angled triangle. The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle. Consider a right-angled triangle, right-angled at B.

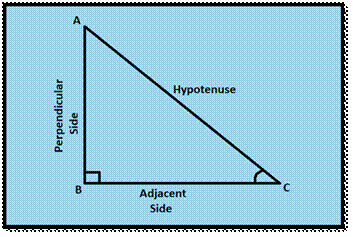
With respect to ∠C, the ratios of trigonometry are given as:

sine: Sine of an angle is defined as the ratio of the side opposite(perpendicular side) to that angle to the hypotenuse.

cosine: Cosine of an angle is defined as the ratio of the side adjacent to that angle to the hypotenuse.

tangent: Tangent of an angle is defined as the ratio of the side opposite to that angle to the side adjacent to that angle.

cosecant: Cosecant is a multiplicative inverse of sine.

secant: Secant is a multiplicative inverse of cosine.

cotangent: Cotangent is the multiplicative inverse of the tangent.

The above ratios are abbreviated as sin, cos, tan, cosec, sec and tan respectively in the order they are described. So, for Δ ABC, the ratios are defined as:

sin C = (Side opposite to ∠C)/(Hypotenuse) = AB/AC

cos C = (Side adjacent to ∠C)/(Hypotenuse) = BC/AC

tan C = (Side opposite to ∠C)/(Side adjacent to ∠C) = AB/AC = sin ∠C/cos ∠C

cosec C= 1/sin C = (Hypotenuse)/ (Side Opposite to ∠C) = AC/AB

sec C = 1/cos C = (Hypotenuse)/ (Side Opposite to ∠C) = AC/BC

cot C = 1/tan C = (Side adjacent to ∠C)/(Side opposite to ∠C)= BC/AB

In right Δ ABC, if ∠A and ∠C are assumed as 30° and 60°, then there can be infinite right triangles with those specifications but all the ratios written above for ∠C in all of those triangles will be same. So, all the ratios for any of the acute angles (either ∠A or ∠C) will be the same for every right triangle. This means that the ratios are independent of lengths of sides of the triangle. Also, check out trigonometric functions to learn about each of these ratios or functions in detail.

Trigonometric Ratios Table

Below is the table where each ratios values are given with respect to different angles, particularly used in calculations.

Angle	0°	30°	45°	60°	90°
Sin C	0	1/2	1/√2	√3/2	1
Cos C	1	√3/2	1/√2	½	0
Tan C	0	1/√3	1	√3	∞
Cot C	∞	√3	1	1/√3	0
Sec C	1	2/√3	√2	2	∞
Cosec C	∞	2	√2	2/√3	1

Exact values of trigonometric functions of widely used angles:

there are some special angles provided with the trigonometric numbers. To simplify the way of calculation of the trigonometric numbers at various angles, reference angles are used which are derived from the primary trigonometric functions. We can derive values in degrees like 0°, 30°, 45°, 60°, 90°, 180°, 270° and 360°. The trigonometric table is given below, which defines all the values of trigonometric ratios.

Angle (in Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
Angle (in Radians)	0	π/6	π/3	π/4	π/2	π	3π/2	2π
Sin	0	1/2	1/√2	√3/2	1	0	-1	0
Cos	1	√3/2	1/√2	1/2	0	-1	0	1
Tan	0	1/√3	1	√3	∞	0	∞	0
Cot	∞	√3	1	1/√3	0	∞	1	∞
Sec	1	2/√3	√2	2	∞	-1	∞	1
Cosec	∞	2	√2	2/√3	1	∞	-1	∞

Basic Trigonometric Identities:

cos ² x+sin ² x=1

sec ² x−tan ²x=1

cosec ² x−cot ² x=1

cos(2nπ+x)=cosx

sin(2nπ+x)=sinx

cos(−x)=cosx

sin(−x)=−sinx

cos(x+y)=cosxcosy−sinx siny

cos(x−y)=cosxcosy+sinx siny

sin(x+y)=sinxcosy+cosx siny

sin(x−y)=sinxcosy−cosx siny

cos ² x=cos ² x−sin ² x=2cos ² x−1=1−2sin ² x=1−tan ² x / 1−tan ² x

sin2x=2cosx.sinx=2tanx / 1+ tan2x

Radian Measure:

The radian is the standard unit of angular measure. An angle’s measurement in radians is numerically equal to the length of a corresponding arc of a unit circle. The relationship or the connection between the arc length and radius of a circle defines radian of a circle. Degree and radian formula used to convert, degree to radian or radian to degree.

Radian=ArcLength / RadiusLength

Radian=Degree×/π / 180

few Degree Measures and their corresponding Radian Measures – 

30°=π / 6

45°=π/4

60°=π/3

90°=π/2

120°=2π/3

135°=3π/4

150°=5π/6

180°=π

210°=7π/6

225°=5π/4

240°=4π/3

270°=3π/2

300°=5π/3

315°=7π/4

330°=11π/6

360°=2π

Question 1:

Convert 220° into radian measure?

Solution:

Given Degree = 220°

Formula is,

Radian =  degree×π180

Radian = 220×π180

Radian = 11×π9

Radian = 3.837

Trigonometric Functions of real numbers:

Trigonometric Functions of real numbers 1 B w(1) A(1,0) w(2) w(t) t 2 x y O Figure 3.8 For applications of trigonometry to the problems in higher mathematics including calculus and to problems in physics and chemistry, scientists required trigonometric functions of real numbers. This was skillfully done by exhibiting a correspondence between an angle and an arc length denoting a real number on a unit circle. Consider a unit circle with the centre at the origin. Let the angle zero (in radian measure) be associated with the point A(1, 0) on the unit circle. Draw a tangent to the unit circle at the point A(1, 0). Let t be a real number such that t is y- coordinate of a point on the tangent line.

For each real number t, identify a point B(x, y) on the unit circle such that the arc length AB is equal to t. If t is positive, choose the point B(x, y) in the anticlockwise direction, otherwise choose it in the clockwise direction. Let θ be the angle subtended by the arc AB at the centre. In this way, we have a function w(t) associating a real number t to a point on the unit circle. Such a function is called a wrapping function . Then s = rθ gives arc length t = θ. Now, define sin t = sin θ and cost = cos θ. Clearly, sin t = sin θ = y and cost = cos θ = x. Using sin t and cost, other trigonometric functions can be defined as functions of real numbers.

Allied Angles:

Two angles are said to be allied when their sum or difference is either zero or a multiple of 90°. The angles — θ, 90° ± θ, 180° ± θ, 270° + θ, 360° —θ etc., are angles allied to the angle θ, if θ is measured in degrees.

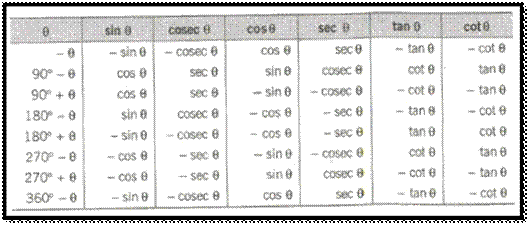
Some Characteristics of Trigonometric Functions:

For example,

Sine and cosine functions are complementary to each other in the sense that sin (90◦ − θ) = cos θ and cos (90◦ − θ) = sin θ.

As cos θ and sin θ are obtained as coordinates of a point on the unit circle, they satisfy the inequalities −1 ≤ cos θ ≤ 1 and −1 ≤ sin θ ≤ 1. Hence, cos θ,sin θ ∈ [−1, 1]

Trigonometric function repeats its values in regular intervals.

Sine and cosine functions have an interesting property that cos (−θ) = cos θ and sin (−θ) = − sin θ

TRIGONOMETRIC IDENTITIES:

Sum and difference identities or compound angles formulas:

A compound angle is an algebraic sum of two or more angles.  We use trigonometric identities to connote compound angles through trigonometric functions. The sum and difference of functions in trigonometry can be solved using the compound angle formula or the addition formula. Here, we shall deal with functions like (A+B) and (A-B). The formula for trigonometric ratios of compound angles are as follows:

sin (A + B)  =  sin A cos B + cos A sin B

sin (A – B)  =  sinA cosB – cosA sinB

cos (A + B)  =  cosA cosB – sinA cosB

cos (A – B)  =  cosA cosB + sinA cosB

tan (A + B)  =  [tanA + tanB] / [1 – tanA tanB]

tan (A – B)  =  [tan A – tan B] / [1 + tan A tan B]

sin(A + B) sin(A – B) = sin² A – sin² B = cos² B – cos² A.

cos(A + B) cos(A – B) = cos² A – sin² A – sin² B = cos² B – sin² A.

Multiple angle identities and submultiple angle identities:

Double Angle Identities :

Sum and difference identities and examine some of the consequences that come from them. Double angle identities are a special case of the sum identities. That is, when the two angles are equal, the sum identities are reduced to double angle identities. They are useful in solving trigonometric equations and also in the verification of trigonometric identities. Further double angle identities can be used to derive the reduction identities (power reducing identities). Also double angle identities are used to find maximum or minimum values of trigonometric expressions.

Triple-Angle Identities Using double angle identities, we can derive triple angle identities.

Identity 3.12: sin 3A = 3 sin A − 4 sin ³ A

Proof.

We have, sin 3A = sin(2A + A) = sin 2A cos A + cos 2A sin A

= 2 sin A cos2 ² A + ( 1 − 2 sin ² A )sin A = 2 sin A
= 2 sin A (1-sin ²A)+ (1- 2 sin ² A)sin A

= 3sin A-4 sin³ A

Submultiples of an Angle

As the name suggests, trigonometric ratio of a submultiple of an angle means when we try to find out some trigonometric value of an angle of the type A/2 or A/3.

Some of the trigonometric identities for the submultiple of an angle are:

| sin A/2 + cos A/2| = √(1 + sin A)

| sin A/2 - cos A/2| = √(1 - sin A)

tan A/2 = ±√(1 - cos A)/(1 + cos A)

Question 1: 

Prove that sinx+sin2x1+cosx+cos2x=tanx

Solution:

Using the identities and formulas above we can solve the question as follows:

sinx+sin2x / 1+cosx+cos2x=tanx

=sinx+2sinxcosx / 2+cos2x+cosx

=sinx(1+2cosx) / cosx(2cos+1)=tanx

Conditional trigonometric identities:

Conditional trigonometric identities we will discuss certain relationship exists among the angles involved. We know some of the trigonometric identities which were true for all values of the angles involved. These identities hold for all values of the angles which satisfy the given conditions among them and hence they are called conditional trigonometric identities.

Such identities involving different trigonometrical ratios of three or more angles can be deduced when these angles are connected by some given relation. Suppose, if the sum of three angles be equal to two right angles then we can establish many important identities involving trigonometrical ratios of those angles. To establish such identities we require to use the properties of supplementary and complementary angles.

If A, B and C denote the angles of a triangle ABC, then the relation A + B + C = π enables us to establish many important identities involving trigonometric ratios of these angles The following results are useful to obtain the said identities.

If A + B + C = π, then the sum of any two angles is supplementary to the third i.e.,

(i) B + C = π - A or, C + A = π - B or A + B = π - C.

(ii) If A + B + C = π then sin (A + B) = sin (π - C) = sin C

sin (B + C) = sin (π - A) = sin A 

sin (C + A) = sin (π - B) = sin B

(iii) If A + B + C = π then cos (A + B) = cos (π - C) = - cos C  
                                  cos (B + C) = cos (π - A) = - cos A
                                  cos (C + A) = cos (π - B) = - cos B

(iv) If A + B + C = π then tan (A + B) = tan (π - C) = - tan C

tan (B + C) = tan (π - A) = - tan A

tan (C + A) = tan (π - B) = - tan B

TRIGONOMETRIC EQUATIONS:

Question 1

Solution 1

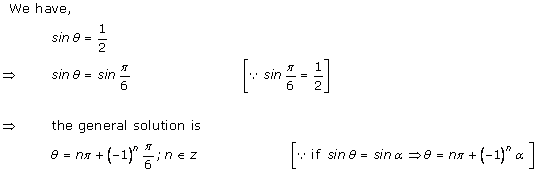
Question 2

Solution 2

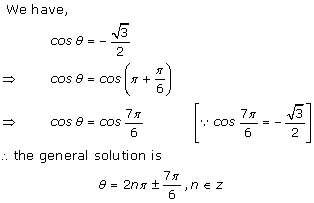
Question 3:

Solution 3:

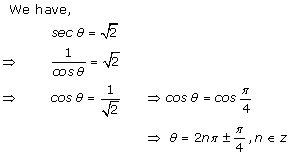
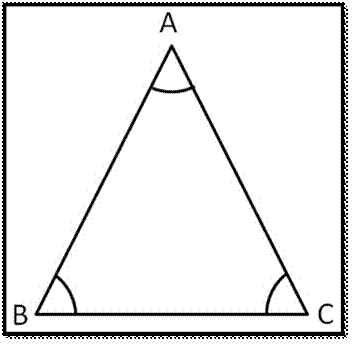
PROPERTIES OF TRIANGLE:

Properties of Triangle One important use of trigonometry is to solve practical problems that can be modeled by a triangle. Determination of all the sides and angles of a triangle is referred as solving the triangle. In any triangle, the three sides and three angles are called basic elements of a triangle. Pythagorean theorem plays a vital role in finding solution of the right triangle. The law of sines and the law of cosines are important tools that can be used effectively in solving an oblique triangle ( a triangle with no right angle). In this section, we shall discuss the relationship between the sides and angles of a triangle and derive the law of sines and the law of cosines. Notation: Let ABC be a triangle. The angles of ABC corresponding to the vertices A, B, C are denoted by A, B, C themselves. The sides opposite to the angles A, B, C are denoted by a, b, c respectively. Also we use the symbol to denote the area of a triangle.

THE LAW OF SINES OR SINE FORMULA:

Law of Sines

In general, the law of sines is defined as the ratio of side length to the sine of the opposite angle. It holds for all the three sides of a triangle respective of their sides and angles.

aSinA=bSinB=cSinC

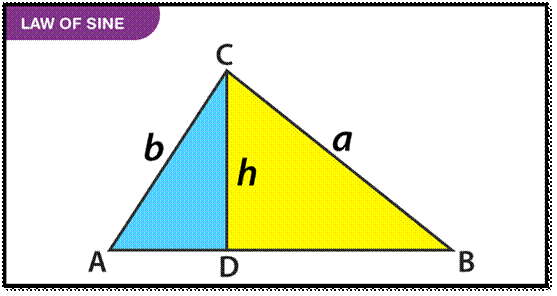
Formula

The formulas used with respect to law of sine are given below.

a / Sin A= b/ Sin B= c / Sin C

a: b: c = Sin A: Sin B: Sin C

a / b = Sin A / Sin B

b / c = Sin B / Sin C

It denotes that if we divide side a by the Sine of ∠A, it is equal to the division of side b by the Sine of∠ B and also equal to the division of side c by Sine of ∠C (Or) The sides of a triangle are to one another in the same ratio as the sines of their opposite angles.

Here, Sin A is a number and a is the length.

Law of Sines Proof

We need a right-angled triangle to prove the above as the trigonometric functions are mostly defined in terms of this type of triangle only.

Given:

△ABC.

Construction: Draw a perpendicular, CD ⊥ AB. Then CD = h is the height of the triangle. “h” separates the △ ABC in two right-angled triangles, △CDA and △CDB.

To Show:

a / b = Sin A / Sin B

Proof:

 In the  △CDA,

Sin A= h/b

And in  △CDB,

Sin B = h/a

Therefore, Sin A / Sin B = (h / b) / (h / a)= a/b

And we proved it.

Similarly, we can prove, Sin B/ Sin C= b / c and so on for any pair of angles and their opposite sides.

Law of Cosines:

In Trigonometry, the law of Cosines, also known as Cosine Rule or Cosine Formula basically relates the length of the triangle to the cosines of one of its angles.

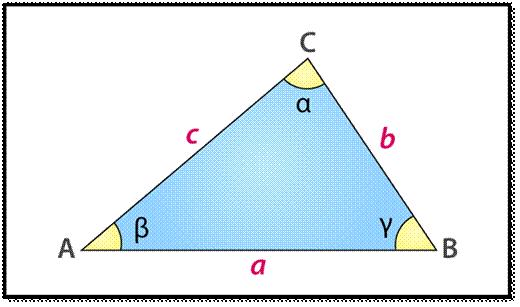
Law of cosines

Law of Cosines Formula

As per the cosines law formula, to find the length of sides of triangle say △ABC, we can write as;

a² = b² + c²– 2bc cos (A)

b² = a² + c² – 2ac cos (B)

c² = a² + b² – 2bc cos (C)

And if we want to find the angles of △ABC, then the cosine rule is applied as;

cos A= (b² + c² – a²)/2bc

cos B = (a² + c²– b²)/2ac

cos C = (a² + b²– c²)/2ab

Where a, b and c are the lengths of legs of a triangle.

Cosines Law Proof

Now let us learn the law of cosines proof here;

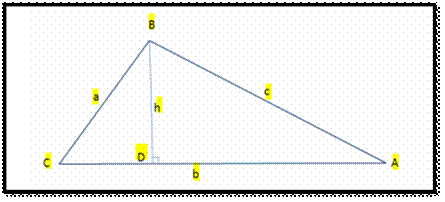
Law of Cosines Proof

In the right triangle BCD, by the definition of cosine function:

cos C = CD/a

or

CD=a cos C

Subtracting above equation from side b, we get

DA = b − acosC ……(1)

In the triangle BCD, according to Sine definition

sin C = BD/a

or

BD = a sinC ……(2)

In the triangle ADB, if we apply the Pythagorean Theorem, then

c² = BD² + DA²

Substituting for BD and DA from equations (1) and (2)

c² = (a sin C)² + (b-acosC)²

By Cross Multiplication we get:

c² = a² sin²C + b² – 2abcosC + a² cos²C

Rearranging the above equation:

c² = a² sin²C + a² cos²C + b² – 2ab cosC

Taking out a² as a common factor, we get;

c² = a²(sin²C + cos²C) + b² – 2ab cosC

Now from the above equation, you know that,

sin²θ + cos²θ = 1

∴ c² = a² + b² – 2ab cosC

Hence, the cosine law is proved.

PROJECTION FORMULA:

The geometrical interpretation of the proof of projection formulae is the length of any side of a triangle is equal to the algebraic sum of the projections of other sides upon it.

2. In any triangle ABC,

(i) a = b cos C + c cos B

(ii)  b = c cos A + a cos C

(iii) c = a cos B +  b cos A

Proof:   

In any triangle ABC we have a 

asinAasinA = bsinBbsinB = csinCcsinC = 2R ……………………. (1)

Now convert the above relation into sides in terms of angles in terms of the sides of any triangle.

a/sin A = 2R

⇒ a = 2R sin A ……………………. (2)

b/sin B = 2R

⇒ b = 2R sin B ……………………. (3)

c/sin c = 2R

⇒ c = 2R sin C ……………………. (4)

(i) a = b cos C + c cos B

Now, b cos C + c cos B

= 2R sin B cos C + 2R sin C cos B

= 2R sin (B + C)

= 2R sin (π - A), [Since, A + B + C = π]

= 2R sin A

= a [From (2)]

Therefore, a = b cos C + c cos B.        Proved.

(ii) b = c cos A + a cos C

Now, c cos A + a cos C

= 2R sin C cos A + 2R sin A cos C

= 2R sin (A + C)

= 2R sin (π - B), [Since, A + B + C = π]

= 2R sin B

= b [From (3)]

Therefore, b = c cos A + a cos C.       

Therefore, a = b cos C + c cos B.        Proved.

(iii) c = a cos B +  b cos A

Now, a cos B + b cos A

= 2R sin A cos B + 2R sin B cos A

= 2R sin (A + B)

= 2R sin (π - C), [Since, A + B + C = π]

= 2R sin C

= c [From (4)]

Therefore, c = a cos B + b cos A.       

Therefore, a = b cos C + c cos B.        Proved.

AREA OF A TRIANGLE :

The area of a triangle is defined as the total space that is enclosed by any particular triangle. The basic formula to find the area of a given triangle is A = 1/2 × b × h, where b is the base and h is the height of the given triangle, whether it is scalene, isosceles or equilateral.

Example: To find the area of the triangle with base b as 3 cm and height h as 4 cm, we will use the formula for:

Area of a Triangle, A = 1/2 × b × h = 1/2 × 4 cm × 3 cm = 2 cm × 3 cm = 6 cm²

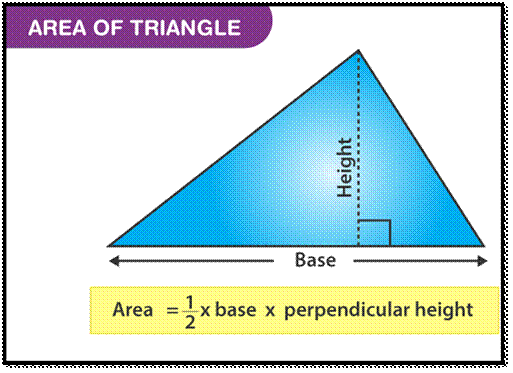
Area of a Triangle Formula

The area of the triangle  is given by the formula mentioned below:

· Area of a Triangle = A = ½ (b × h) square units

where b and h are the base and height of the triangle, respectively.

Heron’s formula :

Heron’s formula is one of the most important concepts used to find the area of a triangle when all the sides are known. Hero of Alexandria was a great mathematician who derived the formula for the calculation of the area of a triangle using the length of all three sides. It is also termed as Hero’s Formula. He also extended this idea to find the area of quadrilateral and also higher-order polygons. This formula has its huge applications in trigonometry such as proving the law of cosines or law of cotangents, etc

Hero’s Formula For Triangle

According to Heron, we can find the area of any given triangle, whether it is a scalene, isosceles or equilateral, by using the formula, provided the sides of the triangle. Suppose, a triangle ABC, whose sides are a, b and c, respectively. Thus, the area of a triangle can be given by;

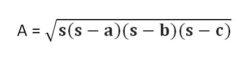
Where “s” is semi-perimeter = (a+b+c) / 2

And a, b, c are the three sides of the triangle.

Example: A triangle PQR has sides a=4, b=13 and c=15. Find the area of the triangle.

Semiperimeter of triangle PQR, s = (4+13+15)/2 = 32/2 = 16

By heron’s formula, we know;

A = √[s(s-a)(s-b)(s-c)]

Hence, A = √[16(16-4)(16-13)(16-15)] = √(16 x 12 x 3 x 1) = √576 = 24

This formula is applicable to all types of triangles. Now let us derive the area formula given by Heron.

APPLICATION TO TRIANGLE:

Trigonometry helps to calculate the correct angle for the triangular support. Also trigonometry envisages the builders to correctly layout a curved structure. For a right triangle, any two information with atleast one side say SS, SA are sufficient to find the remaining elements of the triangle. But, to find the solution of an oblique triangle we need three elements with atleast one side. If any three elements with atleast one side of a triangle are given, then the Law of Sines, the Law of Cosines, the Projection formula can be used to find the other three elements.

Rule:

In a right triangle, two sides determine the third side via the Pythagorean theorem and one acute angle determine the other by using the fact that acute angles in a right triangle are complementary.

If all the sides of a triangle are given, then we can use either cosine formula or half-angle formula to calculate all the angles of the triangle.

If any two angles and any one of the sides opposite to given angles are given, then we can use sine formula to calculate the other sides.

If any two sides of a triangle and the included angle are given, we cannot use the Law of sines; but then we can use the law of cosines to calculate other side and other angles of the triangle. In this case we have a unique triangle.

• All methods of solving an oblique triangle require that the length of atleast one side must be provided.

INVERSE TRIGONOMETRIC FUNCTIONS:

The inverse trigonometric functions are also known as the anti trigonometric functions or sometimes called as arcus functions or cyclometric functions. The inverse trigonometric functions of sine, cosine, tangent, cosecant, secant, and cotangent are used to find the angle of a triangle from any of the trigonometric functions. It is widely used in many fields like geometry, engineering, physics etc. But in most of the time, the convention symbol to represent the inverse trigonometric function using arc-prefix like arcsin(x), arccos(x), arctan(x), arccsc(x), arcsec(x), arccot(x). To determine the sides of a triangle when the remaining side lengths are known.

Consider, the function y = f(x), and x = g(y) then the inverse function is written as g = f^-1,

This means that if y=f(x), then x = f^-1(y).

Such that f(g(y))=y and g(f(y))=x.

Example of Inverse trigonometric functions: x= sin^-1y

The list of inverse trigonometric functions with domain and range value is given below:

Functions	Domain	Range
Sin^-1 x	[-1, 1]	[-π/2, π/2]
Cos^-1x	[-1, 1]	[0, π/2]
Tan^-1 x	R	(-π/2, π/2)
Cosec^-1 x	R-(-1,1)	[-π/2, π/2]
Sec^-1 x	R-(-1,1)	[0,π]-{ π/2}
Cot^-1 x	R	[-π/2, π/2]-{0}