COMBINATORICS
AND MATHEMATICAL INDUCTION
Combinatory has many real life applications where counting of
objects are involved. For example, we may be interested to know if there are
enough mobile numbers to meet the demand or the number of allowable passwords
in a computer system. It also deals with counting techniques and with optimisation methods, that is, methods related to finding
the best possible solution among several possibilities in a real problem. In
this chapter we shall study counting problems in terms of ordered or unordered
arrangements of objects. These arrangements are referred to as permutations and
combinations. Combinatorics are largely used in the counting problems of
Network communications, Cryptography, Network Security and Probability theory.
We shall explore their properties and apply them to counting problems
FUNDAMENTAL PRINCIPLES OF COUNTING
1. The Sum Rule: Let us consider two tasks which need to be completed. If the
first task can be completed in M different ways and the second in N different
ways, and if these cannot be performed simultaneously, then there are M + N
ways of doing either task. This is the sum rule of counting.
2. The Product
Rule: Let us suppose that a task comprises of two procedures. If
the first procedure can be completed in M different ways and the second procedure
can be done in N different ways after the first procedure is done, then the
total number of ways of completing the task is M × N
3. The
Inclusion-Exclusion Principle: Suppose two tasks A and B can be performed simultaneously.
Let n(A) and n(B) represent the number of ways of
performing the tasks A and B independent of each other. Also let n(A ∩ B) be the number of ways of performing the two
tasks simultaneously. We cannot use the sum rule to count the number of ways of
performing one of the tasks as that would lead to over counting. To obtain the
correct number of ways we add the number of ways of performing each of the two
tasks and then subtract the number of ways of doing both tasks simultaneously.
This method is referred to as the principle of inclusion - exclusion. Using the
notation of set theory we write it as
n(A ∪ B) = n(A) + n(B) − n(A ∩ B).
Suppose we have to find the number of positive integers
divisible by 2 or 7 (but not both), upto 1000. Let n(A) denote the number of integers divisible by 2, n(B)
denote the number of integers divisible by 7 and n(A ∩ B) the number of
integers divisible by both 2 and 7. Then the number of positive integers
divisible by 2 or 7 is given by
n(A ∪ B) = n(A) + n(B) − n(A ∩ B) = 500 + 142
− 71 = 571.
(Note that n(A) will include all
multiples of 2 upto 1000, n(B) will include all
multiples of 7 upto 1000 and so on.)
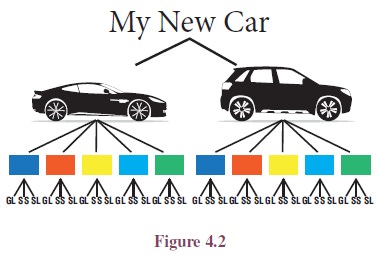
TREE DIAGRAMS:
Tree diagrams are often helpful in representing the
possibilities in a counting problem. Typically in a tree the branches represent
the various possibilities. For example, suppose a person wants to buy a Car for
the family. There are two different branded cars and five colours
are available for each brand. Each colour will have
three different variant on it namely GL,SS,SL. Then
the various choices for choosing a car can be represented through a tree
diagram as follows:
FACTORIALS
Factorial of a natural number n is the product of the first n
natural numbers. It is denoted by n!.
That is,
n!=1 × 2 × 3 ×···× n.
We read this symbol as “n factorial” or “factorial
of n”. The notation n! was
introduced by the French mathematician Christian Kramp
in the year 1808. Note that for a positive integer n
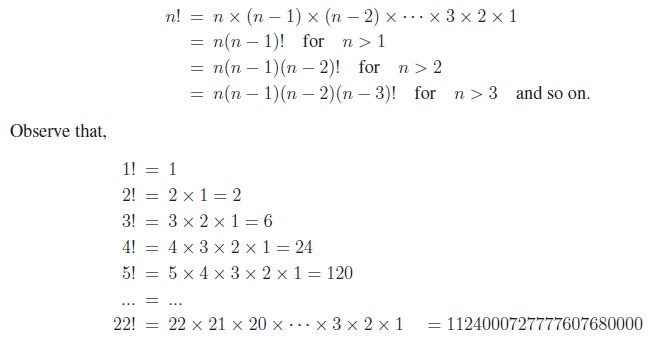
The number 22 ( the Birth date of
Ramanujan) has a special place with respect to factorial that, it is the least
integer N greater than 1 whose factorial has exactly N digits.
It will be a good exercise for both students and teachers to
find the next number N such that N! has exactly N digits.
Note that 0! = 1 is evident by substituting n =
0 in the equation (n + 1)! = (n + 1) × n! as 1! = (0 + 1) × 0! ⇒ 0! = 1! / 1 = 1.
This way, we talk of factorial for non-negative integers. Note that
factorials can be extended to certain negative numbers and also to complex
numbers, which are beyond the scope of this book.
We shall now discuss certain examples in order to familiarise the computation of factorials.
PERMUTATIONS
What is a permutation ?
Permuations come in various disguises.
Suppose three friends A, B and C have to stand in line for a
photograph. In how many order can they stand? Some of the possible arrangements
(from left to right) are
A, B, C: A, C, B: B, A, C
B, C, A: C, B, A: C, A, B.
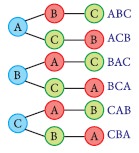
Thus there are six possible ways in which they can arrange
themselves for the photograph.
Thus if 3 objects have to be arranged in a row there
are 3 × 2 × 1 = 3! possible permutations. The number of permutations of 4
objects taken all at a time is 4 × 3 × 2 × 1
= 4! Thus if n objects have to be arranged in a line
there are n × (n − 1) × (n − 2) ×
· · · × 3 × 2 × 1 = n! possible arrangements or permutations.
Suppose you have 7 letters A,B,C,D,E,F
and G. We want to make a 4 letter string. We have 7 choices for the 1st letter.
Having chosen the first letter, we have 6 choices for the second letter.
Proceeding this way, we have 4 choices for the 4th letter.
Hence, the number of permutations of 4 letters chosen from 7
letters is
1. Permutations of distinct objects
In terms of function on any finite set say S = {x1,
x2, ...xn}, a permutation can be defined as
a bijective mapping on the set S onto itself. The number of
permutation on the set S is the same as the total number of
bijective mappings on the set S.
We denote the number of permutations by nPr.
1. If n, r are
positive integers and r ≤ n, then the
number of permutations of n distinct objects taken r at
a time is n (n − 1) (n − 2) ·
· · (n − r + 1).
Proof.
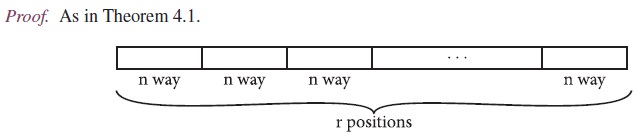
A permutation is an ordering. A permutation of n distinct objects taken r at a time is formed by filling of r positions,
in a row with objects chosen from the given n distinct
objects.
There are n objects that can be filled in the first
position. For the second position there are remaining n − 1 objects.
There are n − 2 objects for the third
position. Continuing like this until finally we place one of the (n − (r − 1)) possible
objects in the rth position.
By the rule of product we conclude nPr = n (n − 1)
(n − 2) · · · (n − r +
1).
Theorem 4.3: The number of
permutations of n different objects taken r at a time where
repetition is allowed, is nr.
We can fill the first position with n objects.
For the second position (still we can use the object used in first position),
there are n objects, and so on the rth position
can be filled with n objects.By the
rule of product, The number of permutations of n different
objects taken r at a time when repetition allowed is n × n × n ×
· · · n (r times) = nr
2. Properties of Permutations
3. Objects always together (String method)
The number of permutations of n different objects, taken all at a time, when m specified objects are always together,
Consider a string of m specified
objects as a single unit
Then we have (n − m +
1) objects. Permute this (n − m +
1) objects in (n − m +
1)! ways.
Then permute the m specified
objects between themselves in m! ways.
Finally, the answer is m! × (n − m +
1)!.
4. No two things are together (Gap method)
To obtain the number of permutations of n different objects when no two of k given objects occur together and there are no restrictions
on the remaining m = n − k objects, we follow the procedure as follows:
First of all, arrange the m objects
on which there is no restriction in a row. These m objects can be permuted
in mPm = m! ways.
Then count the number of gaps
between every two of m objects on which there is no
restriction including the end positions. Number of such gaps will be one more
than m that is (m + 1). In this m +
1 gaps, we can permute the k objects in m+1Pk ways.
Then the required number of
ways are m! ×(m+1) Pk
5. Permutations of not all distinct objects
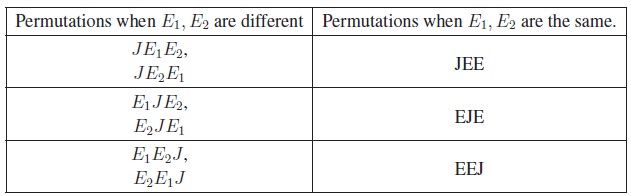
Consider permuting the letters of the word JEE. In this case the
letters of the word are not different. There are 2 E’s, which are of same kind.
Let us treat, temporarily, the 2 E’s as different, say E1 and E2.
The number of permutations of 3 different letters taken all at a time is 3!.
COMBINATIONS
Let us suppose there are four persons A, B, C and D (actual
names may be used here) and we have to select three of them to be a part of a
committee. In how many ways can we make this selection? For example, A,
B, C is one possible choice. Here the order of selection is
immaterial. Thus A, B, C is the same as B, A, C or C,
A, B as long as the same three persons are selected. Thus the possible
distinct choices or selections are A, B, C; A, B, D; A,
C, D and B, C, D. We may thus conclude that there are 4
ways of selecting 3 people out of 4. Each choice or selection is referred to as
a combination of 4 different objects taken 3 at a time.
Suppose two persons are to be selected from four persons. The
possible choices are: A, B : A, C: A, D : B,
C : B, D : C, D. Thus the number of
combinations of 4 different objects taken 2 at a time is 6.
The number of combinations of n different objects taken r at
a time is represented by nCr.
From the above we may conclude that 4C3 =
4 and 4C2 = 6. Now, 4C3 is
the number of combinations of 4 objects taken 3 at a time.
Note that in each combination, the three objects may be arranged
in 3! ways.
Thus the total number of permutations of 4 objects taken 3 at a
time is 4C3 × 3!. This is also equal to 4P3.
Hence 4P3 =4 C3 × 3!.
1. Properties of Combinations
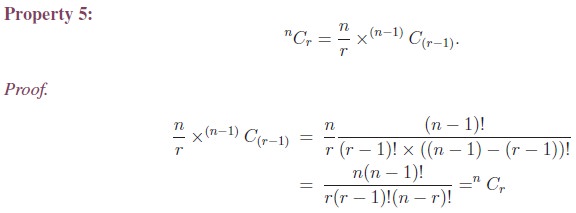
MATHEMATICAL INDUCTION
Let us consider the sum of the first n positive odd numbers.
These are 1, 3, 5, 7, ·
· · , 2n − 1.
The first odd number 1 which is equal to 1. The first two odd
numbers are 1 and 3 and their sum is 4. Writing these
as follows helps us to see a pattern.
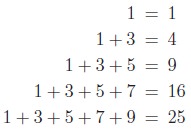
and so on. We note that the
right hand side of the expressions are the perfect squares 1, 4, 9, 16, 25 ·
· · .
This pattern compels us to make the conjecture that the sum of the first n odd
numbers is equal to n2. Symbolically, we express this
as,
1 + 3 + 5 + · · · + (2n − 1)
= n2.
However we have only made a conjecture. In order to prove the
conjecture we shall use the Principle of Mathematical Induction. Mathematical
Induction is a method or technique of proving mathematical results or theorems
of the above kind. This technique relies upon making conjectures by observing
all possible cases of a specific result. It is well suited for proving results
in algebra or in other disciplines of mathematics where results or theorems are
stated in terms of n, n being a positive integer.
The process of Mathematical Induction may be compared to that of climbing an
infinite staircase.
In order to ensure that we complete the climb, it is sufficient
to ensure the following.
a. We can climb the first step.
b. Once we have reached a
particular step of the staircase, we can climb to the next step.
Being sure of (a) and (b) will enable us to climb all the steps
in the staircase. Similarly, when we apply this method to prove a mathematical
statement P (n), the process of induction involves the
following steps.
One of the interesting method of proof in Mathematics is by the
Mathematical induction. We shall illustrate the method through problems. As an
illustration of the process let us revisit a well known result through an
example below:
