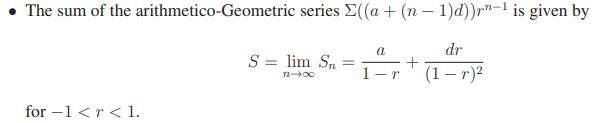Binomial Theorem, Sequences and Series

Introduction

· Binomial theorem facilitates the algebraic expansion of the binomial (a + b) for a positive integral exponent n.

· Greek Mathematician Euclid mentioned the special case of binomial theorem for exponent 2. Binomial theorem for exponent 3 was known by 6th century in India. In 1544, Michael Stifel (German Mathematician) introduced the term binomial coefficient and expressed (1 + x)ⁿ in terms of (1 + x)ⁿ⁻¹.

Binomial Theorem

The prefix bi in the words bicycle, binocular, binary and in many more words means two. The word binomial stands for expressions having two terms. For examples (1 + x), (x + y),

(x² + xy) and (2a + 3b) are some binomial expressions.

Binomial Coefficients

We know that

Since occurs as the coefficients of x^r in (1 + x)ⁿ n ∈ N and as the coefficients of a^r b^n−r in (a + b)ⁿ, they are called binomial coefficients.

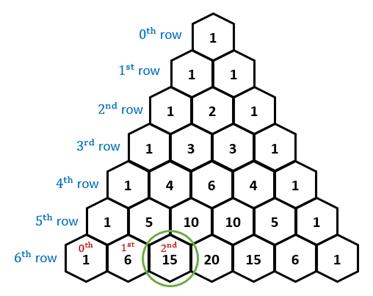
Pascal Triangle

The Pascal triangle is an arrangement of the numbers in a triangular form. The (k + 1)^st row consists of the numbers.

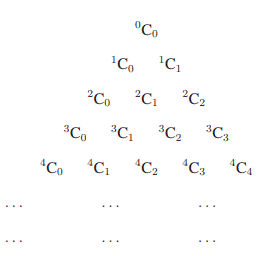
The Binomial Expansion of (a + b)ⁿ

(a + b)ⁿ =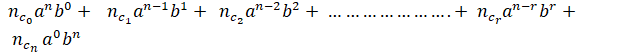

which is the binomial expansion of (a + b)ⁿ. The binomial expansion of (a + b)ⁿ for any n ∈ N can be written using Pascal triangle

For example, (a + b)⁵ =

Binomial theorem for positive integral index

If n is any positive integer, then

(a + b)ⁿ =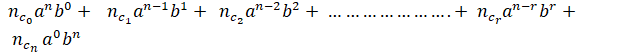

Observation –

(i) The expansion of (x + a)ⁿ, n ∈ N can also be written as

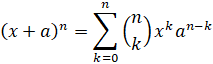
(ii) The expansion of (a + b)ⁿ, n ∈ N, contains exactly (n + 1) terms.

(iii) In , the powers of x decreases by 1 in each term, whereas the powers of a increases by 1 in each term. However, the sum of powers of x and a in each term is always n.

(iv) The (r + 1)^th term in the expansion of (a + b)ⁿ, n ∈ N, is

(v) In the product (a + b)(a + b)···(a + b), n times, to get br, we need any r factors out of these n factors. This can be done in nCr ways. That is why, we have nCr as the coefficient of a^n−r b^r .

(vi) In the expansion of (a + b)ⁿ, n ∈ N, the coefficients at equidistant from the beginning and from the end are equal due to the fact that ⁿC_r = ⁿC_n−r .

(vii) In the expansion of (a + b)ⁿ, n ∈ N, the greatest coefficient is ⁿC _n/2 if n is even and the greatest coefficients are ⁿC _{n−1/ 2} or ⁿC _n+1/2 , if n is odd.

(viii) In the expansion of (a + b)ⁿ, n ∈ N, if n is even, the middle term is = ⁿC _n/2 a ^{n− n/2} b ^n/2 . If n is odd, then the two middle terms are and .

Example - Find the middle term in the expansion of (x + y)⁶.

Sol: Here n = 6; which is even.

Thus the middle term in the expansion of (x+y)⁶ is the term containing x ^6/2 y ^6/2 , that is the term ⁶C₃ x³y³ which is equal to 20x³y³.

Finite Sequences

· If X is any set and n ∈ N, then any function f : {1, 2, 3,...,n} → X is called a finite sequence on X and any function g : N → X is called an infinite sequence on X. The value f(n) of the function f at n is denoted by a_n and the sequence itself is denoted by (a_n).

· If the set X happens to be a set of real numbers, the sequence is called a numerical sequence or a sequence of real numbers.

· Though every sequence is a function, a function is not necessarily a sequence.

· Unlike sets, where elements are not repeated, the terms in a sequence may be repeated. In particular, a sequence in which all terms are same is called a constant sequence.

· A useful way to visualise a sequence (a_n) is to plot the graph of {(n, a_n) : n ∈ N} which gives some details about the sequence.

Arithmetic Progression (AP)

A sequence of the form

a, a + d, a + 2d, a + 3d, . . . , a + (n − 1)d, a + nd, . . .

is called an arithmetic progression or an arithmetic sequence. In other words, each term (other than the first term) of the sequence is obtained by adding a constant to its previous term; the constant d is called common difference and the term a is called the initial term or first term.

The nth term of an arithmetic progression is given by T_n = a + (n − 1)d.

• The sequences √2, √2 + √3, √2+2√3, √2+3√3, ... and 12, 9, 6, 3, ... are arithmetic sequences with common differences √3 and −3 respectively.

• It is interesting to observe that 3, 7, 11 are three prime numbers which form an AP.

• For n ∈ N, T_n = an + b where a and b are relatively prime, form an AP which contains infinitely many prime numbers along with infinitely many composite numbers.

Geometric Progression (GP)

• A sequence of the form

a, ar, ar² , ar³ , . . . , ar ⁿ⁻¹ , arⁿ, ... with a ≠ 0, and r ≠0

is called a geometric progression or a geometric sequence. In other words, each term (other than the first term) of the sequence is obtained by multiplying its previous term by a constant; the constant r is called common ratio and the term a is called the initial term or first term.

• The nth term of a geometric progression is given by T_n = ar ⁿ⁻¹.

• The sequences 1, 2, 4, 8, 16, ... and √2, 2, 2 √2, 4, 4 √2, 16, ... are geometric sequences with common ratios 2 and √2 respectively.

• Taking logarithm of each term in a geometric progression with positive common ratio yields an arithmetic progression. i.e., If a, ar, ar²,... is a GP with r > 0, then log a, log(ar), log(ar²),... is an AP with common difference log r.

Arithmetico-Geometric Progression (AGP)

A sequence of the form

a, (a + d)r, (a + 2d)r² , (a + 3d)r³ , ..., (a + (n − 1)d)r ⁿ⁻¹ , (a + nd)rⁿ, ......

is called an arithmetico-geometric progression or an arithmetico-geometric sequence.

Harmonic Progression (HP)

A sequence h₁, h₂, h₃ ,... is said to a harmonic sequence or a harmonic progression if , ..... is an arithmetic sequence.

Example - If the 5th and 9th terms of a harmonic progression are 1/19 and 1/35, find the 12th term of the sequence.

Sol: Let h_n be the harmonic progression and let a_n = , Then a₅ = 19 and a₉ = 35. As a_n’s from an arithmetic progression,

we have a + 4d = 19 and a + 8d = 35.

Solving these two equations, we get

a = 3 and d = 4. Thus

a₁₂ = a + 11d = 47.

Thus the 12th term of the harmonic progression is 1/47.

Arithmetic Mean

Let n be any positive integer. Let a₁, a₂, a₃,...,a_n be n numbers . Then the number

is called the arithmetic mean of the numbers a₁, a₂, a₃,...,a_n.

Geometric Mean

Let n be any positive integer. Let a₁, a₂, a₃,...,a_n be n non-negative numbers. Then the number

is called the geometric mean of the numbers a₁, a₂, a₃,...,a_n.

Theorem - If AM and GM denote the arithmetic mean and the geometric mean of two nonnegative numbers, then AM ≥ GM. The equality holds if and only if the two numbers are equal.

Important Result - If a₁, a₂, a₃,...,a_n is a geometric progression, every term a_k (k > 1) is the geometric mean of its immediate predecessor a _k−1 and immediate successor a _k+1.

Harmonic Mean

The harmonic mean of a set {h₁, h₂,...,h_n} of positive numbers is defined as

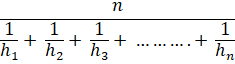
Theorem - If GM and HM denote the geometric mean and the harmonic mean of two nonnegative numbers, then GM ≥ HM. The equality holds if and only if the two numbers are equal.

We know that AM ≥ GM and now we have GM ≥ HM. Combining these two, we have an important inequality AM ≥ GM ≥ HM.

Result - For any two positive numbers, the three means AM, GM and HM are in geometric progression.

Note –

• If b is the arithmetic mean of a and c, then a, b, c is an arithmetic progression.

• If b is the geometric mean of a and c, then a, b, c is a geometric progression.

• If b is the harmonic mean of a and c, then a, b, c is a harmonic progression.

Finite Series

If (a_n) is a sequence of numbers, then the expression a₁ + a₂ + ··· + a_n is called a finite series.

Sum of Arithmetic Progressions

• A series is said to be an arithmetic series if the terms of the series form an arithmetic sequence.

• The sum S_n of the first n terms of the arithmetic sequence (a + (n − 1)d) is given by S_n = na + d = [2a + (n − 1)d].

Sum of Geometric Progressions

· A series is said to be a geometric series if the terms of the series form a geometric sequence.

· The sum S_n of the first n terms of the geometric sequence (ar ⁿ⁻¹) is given by S_n = provided r ≠ 1. If r = 1, then the sequence is nothing but the constant sequence a, a, a, . . . and the sum of the first n terms is clearly na. Thus, if r ≠ 1, then 1 + r + r² + ··· + r ⁿ⁻¹ = .

Sum of Arithmetico-Geometric Progressions

• A series is said to be an arithmetico-Geometric series if the terms of the series form an arithmetico-Geometric sequence.

• The sum S_n of the first n terms of the arithmetico-Geometric sequence ((a + (n − 1)d)r ⁿ⁻¹) is given by

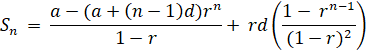
Telescopic Summation for Finite Series

Telescopic summation is a more general method used for summing a series either for finite or infinite terms. This technique expresses sum of n terms of a given series just in two terms, usually first and last term, by making the intermediate terms cancel each other. After canceling intermediate terms, we bring the last term which is far away from the first term very close to the first term. So this process is called “Telescopic Summation”.

Infinite Sequences and Series

Fibonacci Sequence

The Fibonacci sequence is a sequence of numbers where a number other than first two terms, is found by adding up the two numbers before it. Starting with 1, the sequence goes

1, 1, 2, 3, 5, 8, 13, 21, 34, and so forth.

Written as a rule, the expression is x_n = x _n−1 + x _n−2, n ≥ 3 with x₀ = 1, x₁ = 1.

Infinite Series

Let be a series of real numbers and let

s_n = a₁ + a₂ + a₃ + ··· + a_n, n ∈ N

The sequence (s_n) is called the partial sum sequence of . If (s_n) converges and if = s, then the series is said to be a convergent series and s is called the sum of the series.

Infinite Geometric Series

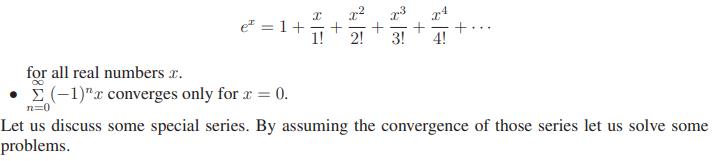
Infinite Arithmetico-Geometric Series