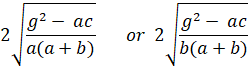Two Dimensional Analytical Geometry
Introduction
·
Francois viete(1540-1603)
introduced the first systematic algebraic notation and contributed to the
theory of equations.
·
Two French
mathematicians-philosophers Rene Descartes ´ and Pierre de Fermat independently
founded analytical geometry in the-1630s by adapting Francois viete’s algebra
to the study of geometric loci.
·
The problem of the shortest line
plays a chief and historically important role in the foundations of geometry.

Locus of a
point
·
A point is an exact position or location
on a plane surface.
·
The path traced out by a moving
point under certain conditions is called the locus of that point.
Alternatively, when a point moves in accordance with a geometrical law, its
path is called locus. The plural of locus is loci.
Illustration 1
In cricket, when a ball is bowled by a bowler, the
path traced out by the ball is the locus of the ball. Whenever there is dispute
between batsmen and the fielders for leg before wicket (LBW) decisions, the
locus of the ball solves the crises, raised by the players for review, through
the third umpire. The likely path of the ball can be projected forward, through
the batsman’s legs, to see whether it would have hit the stumps or not.
Consultation of the third umpire, for conventional slow motion or HawkEye, the
probable decision will be taken. This method is currently sanctioned in
international cricket.

Illustration
2
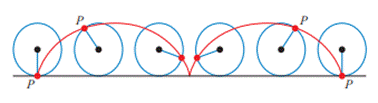
Suppose P be a point on
the rim (circumference) of a circular wheel. When the circle is rolling without
slipping along a straight line, the locus of the point P on the rim is shown in
figure. The path traced out by the point P is known as cycloid.
Illustration
3
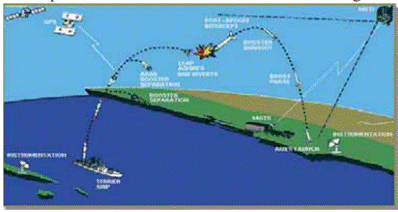
A missile is launched from
the army ship to attack and another from the land to intercept it. The loci of
the missiles are shown in figure.
Procedure
for finding the equation of the locus of a point
(i) If we are finding the
equation of the locus of a point P, assign coordinates, say (h, k) to P
(ii) Express the given
conditions as equations in terms of the known quantities and unknown
parameters.
(iii) Eliminate the parameters, so that the
resulting equation contains only h, k and known quantities.
(iv) Replace h by x, and k
by y, in the resulting equation. The resulting equation is the equation of the
locus of point P.
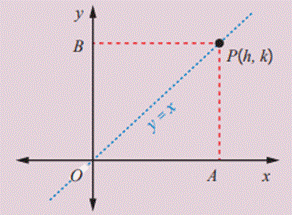
Example - Find the locus of a point which moves such that its distance from the x-axis is equal to the distance from the y-axis.
Sol: Let P (h,
k) be a point on the locus.
Let A and B be the foot of the perpendiculars
drawn from the point P on the x-axis and the y-axis respectively.
Therefore P is (OA,
OB)=(BP, AP)=(h, k)
Given that AP = BP ⇒ k = h
replacing h and k by
substituting h = x and k = y
The locus of P is, y = x
, is a line passing through the origin
·
Whenever the parameters are in
trigonometric form, try to use trigonometric identities to eliminate θ
sin2
θ + cos2 θ = 1, sec2 θ − tan2
θ = 1, cosec2θ − cot2 θ = 1.
Straight Lines
Linear equations can be rewritten using the laws
of elementary algebra into several different forms. These equations are often
referred to as the “equations of the straight line.” In the general form the
linear equation is written as:
ax + by + c = 0
where a and b are not both equal to zero. The name
“linear” comes from the fact that the set of solutions of such an equation
forms a straight line in the plane.
The
relationship between the angle of inclination and slope
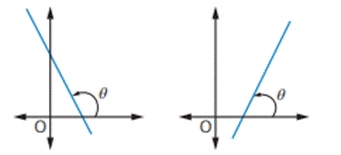
The angle of inclination of a straight line is the
angle, say θ, made by the line with the x-axis measured in the counter
clockwise (positive) direction.
The slope or gradient of a straight line is a
number that measures its “direction and steepness”.
The slope of a line in the plane containing the x
and y axes, is generally represented by the letter m. It can be measured in
many ways as given below:
(i) When
θ is the angle of inclination of the line with the x-axis measured in the
counter clockwise direction then the slope
![]()
![]()
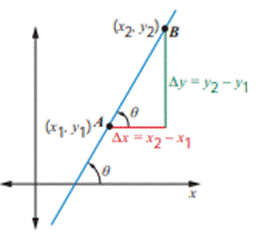
(ii) When (x1, y1) and (x2,
y2) are any two points on the line with x2 ≠ x1, then the
slope is the change in the y coordinate divided by the corresponding change in
the x coordinate. This is described by the following equation.
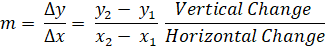
(iii) When the general form of the linear equation
ax + by + c = 0 is given, then the slope of the line is
![]()
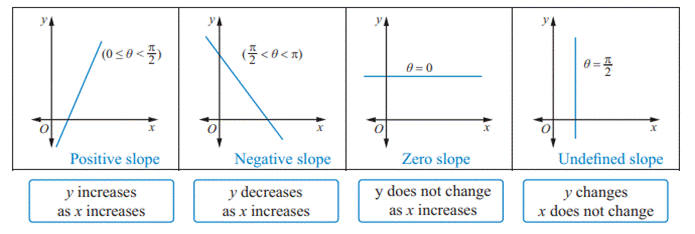
The slope of a line can be a positive or negative
or zero or undefined as shown below:
In a plane three or more points are said to be
collinear if they lie on a same straight line.
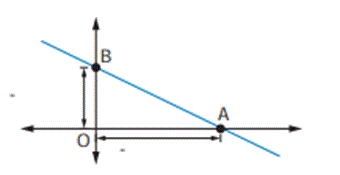
Intercepts of a Line
The intercept of a line is the point at which the
line crosses either the x-axis or the y-axis.
(i) the equation of the y-axis is x = 0.
(ii) the equation of the x-axis is y = 0.
In the figure OA is the x-intercept and OB is the
y-intercept.
Different Forms
of an equation of a straight line
(i) Slope and intercept form
(ii) Point and Slope form
(iii) The two Point form
(iv) Intercepts form
(v) Normal
form
(vi) Parametric form
Slope and Intercept form
![]()
(1) when b = 0 and m ≠ 0, the line passes
through the origin and its equation is y = mx.
(2) when b = 0 and m = 0, the line coincides with
the x-axis and its equation is y = 0.
(3) when b ≠ 0 and m = 0, the line is
parallel to the x-axis and its equation is y = b.
Point - Slope form
![]()
![]()
Since, the slope m is undefined for lines parallel
to the y-axis, the point-slope form of the equation will not give the equation
of a line through A (x1, y1) parallel to the y-axis.
However, this presents no difficulty, since for any such line the abscissa of any
point on the line is x1. Therefore, the equation of such a line is x
= x1.
Two Points form
![]()
Intercepts form:
![]()
Normal form:
![]()
Parametric form:
![]()
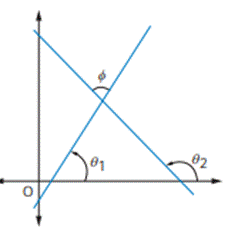
Angle between
two straight lines
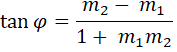
Condition for Parallel Lines
![]()
(i)
The lines parallel to ax + by + c = 0 are of the form ax + by = k.
(ii)
The line parallel to ax + by + c = 0 and passing through a point (x1,
y1), then its equation is ax + by = ax1 + by1.
Condition for perpendicular Lines
![]()
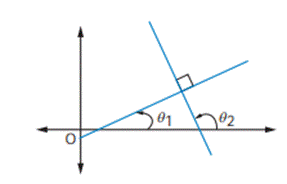
(i) The perpendicular line to ax + by + c = 0 are
of the form bx − ay = k.
(ii) The perpendicular line to ax + by + c = 0 and
passes through the point (x1, y1), then the required
equation is bx − ay = bx1 − ay1.
Position of a
point with respect to a straight line
Any line ax + by + c =0(c ≠ 0),divides the
whole plane in to two parts:
(i) one containing the origin called origin side
of the line and
(ii) the other not containing the origin called
non-origin side of the line.
A point P (x1, y1) is on the
origin side or non-origin side of the line ax + by + c =0(c ≠ 0),
according as ax1 + by1 + c and c are of the same sign or
opposite sign.
If c > 0, then P (x1, y1)
is on the origin side or non orign side of the line ax + by + c = 0 , according
as ax1 + by1 + c is positive or negative.
Distance
Formulas
(i) The distance between two points (x1,
y1) and (x2, y2) is given by the formula
![]()
(ii) The distance from a point P (x1, y1)
to a line ax + by + c = 0 is
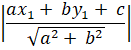
(iii) The distance between two parallel lines a1x
+ b1y + c1 = 0 and a1x + b1y + c2
= 0 is
![]()
Family of lines
One condition yields a linear relation among two
arbitrary constants and hence each arbitrary constant determines the other.
Therefore, the lines which satisfy one condition contain a single arbitrary
constant. Such a system of lines is called one parameter family of lines and
the unknown arbitrary constant is called, the parameter.
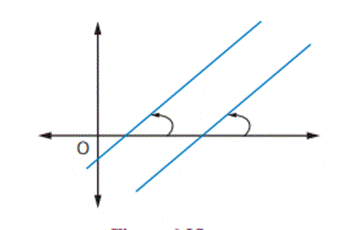
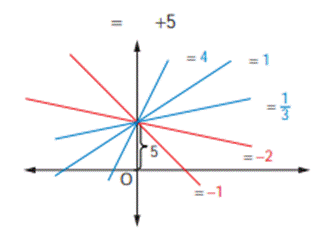
One parameter families
(i) when m is arbitrary and b is a fixed constant
Let us find the family of equations of straight
lines for the line y = m x + b by considering m is arbitrary constant and b is
a fixed constant say b = 5. Therefore the equation, for different real values
of m, represents a family of lines with y-intercept 5 units. A few members of
this family are shown in figure.
(ii) when b is arbitrary and m is a fixed
constant.
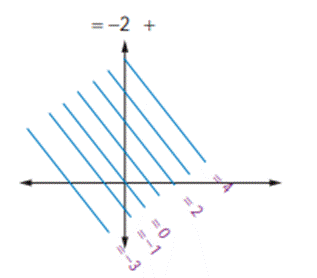
Family of parallel lines: Family of parallel lines
to ax+by +c = 0 is of the form ax+by +λ = 0. For different values of
λ , we get different lines parallel to ax + by + c = 0.
Family of perpendicular lines: Family of
perpendicular lines to ax + by + c = 0 is of the form bx − ay + λ =
0. For different values of λ, we get different lines perpendicular to ax +
by + c = 0.
Two parameters families
Let
L1 ≡ a1x + b1y + c1 = 0 and L2
≡ a2x + b2y + c2 = 0, be the equation of
two given lines. The family of equations of straight lines through the point of
intersection of the above lines is
L1
+ λL2 = 0 where λ is a parameter. That is, for
different real values of λ we get different equations.
Pair of Straight Lines
Let L1 ≡ a1x + b1y
+ c1 = 0 and L2 ≡ a2x + b2y +
c2 = 0, be separate equations of two straight lines. If P (x1,
y1) is a point on L1, then it satisfies the equation L1 =
0. Similarly, if P (x1, y1) is on L2 then L2
= 0. If P (x1, y1) lies either on L1 = 0 or L2
= 0, then P (x1, y1) satisfies the equation (L1
) (L2)=0, and no other point satisfies L1 ·L2
= 0. Therefore the equation L1 ·L2 = 0 represents the
pair of straight lines L1 = 0 and L2 = 0.
Angle between Pair of Straight Lines
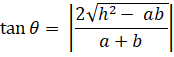
As a consequence of this formula, we can conclude
that
1. The lines are real and distinct, if m1
and m2 are real and distinct, that is if h2 − ab
> 0
2. The lines are real and coincident, if m1
and m2 are real and equal, that is if h2 − ab = 0
3. The lines are not real (imaginary), if m1
and m2 are not real, that is if h2 − ab < 0
Also, we see that the lines are parallel (since both pass through the
origin, the lines are coincident lines) if tan θ = 0, that is h2
− ab = 0, and perpendicular if cot θ = 0 that is a + b = 0.
Equation of the bisectors of the
angle between the lines ax2 + 2hxy + by2 = 0
![]()
General form of Pair of Straight
Lines
ax2 + 2hxy + by2
+ 2gx + 2fy + c = 0
The above equation is a non homogenous equation of
degree two.
Condition that the general second degree equation
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 should represent a
pair of straight lines
abc + 2fgh − af 2 − bg2 − ch2 =
0
Results
(i)
Two straight lines represented by the equation ax2 + 2hxy + by2
+ 2gx + 2fy + c = 0 are parallel if
![]()
(ii) If ax2 + 2hxy + by2 +
2gx + 2fy + c = 0 represents a pair of parallel straight lines, then the
distance between them is