PROBABILITY DISTRIBUTIONS

History

The history of random variables and how they evolved into mapping from sample space to real numbers was a subject of interest. The modern interpretation certainly occurred after the invention of sets and maps (1900), but as Eremenko says, random variables were used much earlier. Mathematicians felt the need to interpret random variables as maps. In 1812, Laplace published his book on Theory analytique des probabilities in which he laid down many fundamental results in statistics.

1.PNG

Random Variable

A random variable X is a function defined on a sample space S into the real numbers R such that the inverse image of points or subset or interval of R is an event in S, for which probability is assigned.

2.PNG

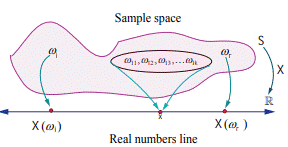
Illustration 1

                 Suppose a coin is tossed once. The sample space consists of two sample points H (head) and T (tail).

                                            That is S = { T, H }

                                            Let   X : S R  be the number of heads

                                       Then X(T) = 0 and X(H) = 1

Thus X is a random variable that takes on the values 0 and 1. If X (ω) denotes the number of heads, then

                                                             

3.gif

Illustration 2

            A batch of 150 students is taken in 4 buses to an excursion. There are 38 students in the first bus, 36 in second bus, 32 in the third bus, and the remaining students in the fourth bus. When the buses arrive at the destination, one of the 150 students is randomly chosen. Suppose that X denotes the number of students on the bus of that randomly chosen student. Then X takes on the values 32, 36, 38, and 44.

Illustration 3

           A coin is tossed until head occurs. 

           The sample space is S = {H,TH,TTH,TTTH,……….}.

            Suppose X denotes the number of times the coin is tossed until head occur.

           Then the random variable X takes on the values 1 2, ,3,……………

Illustration 4

 Suppose N is the number of customers in the queue that arrive at a service desk during a time period, then the sample space should be the set of non-negative integers. That is S = { 0, 1,2, 3….. } and N is a random variable that takes on the values 0,1,2, 3,…..

Illustration 5

                     If an experiment consists in observing the lifetime of an electrical bulb, then a sample space would be the life time of electrical bulb. Therefore the sample space is S ­= [0, . Suppose X denotes the lifetime of the bulb, then X is a random variable that takes on the values in .

Illustration 6

                Let D be a disk of radius r. Suppose a point is chosen at random in D. Let X denote the distance of the point from the centre. Then the sample space S = D and X is the random variable that takes any number from 0 to r. That is

 

Types of Random Variable

       Discrete random variables

                A random variable X is defined on a sample space S into the real numbers R is called discrete random variable if the range of X is countable, that is, it can assume only a finite or countably infinite number of values, where every value in the set S has positive probability with total one.

        Probability Mass Function

             If X is a discrete random variable with discrete values x1,x2,x3,……….. then the function denoted by f (.) or p(.) and defined by

            f(xk) = P(X = Xk) ,    for k = 1,2,3……  is called the probability mass function of X.

    Example  Two fair coins are tossed simultaneously (equivalent to a fair coin is tossed twice). Find the probability mass function for number of heads occurred.

     Sol:   The sample space S = {H,T} x {H,T}

               That is S = {TT,HT,TH,HH}

 Let X be the random variable denoting the number of heads. Therefore

                       X(TT) = 0          X(TH) = 1              X(HT) = 1            X(HH) = 2

 Then the random variable X takes on the values 0, 1 and 2

 3.PNG

The probabilities are given by

                f(0) = P(X = 0) =

                f(1) = P(X = 1) =

               f(2) = P(X = 2) =

              The function f (x) satisfies the conditions

                (i) f(x) ≥ 0 for x = 0,1,2

                (ii)  =  = f(0) + f(1) + f(2)   =  = 1

Therefore f (x) is a probability mass function given by

                                        5.PNG

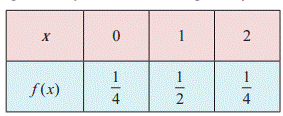
Cumulative Distribution Function or Distribution Function with probability mass function

       The cumulative distribution function F (x) of a discrete random variable X , taking the values x1,x2,x3,…. such that x1<x2<x3<……  with probability mass function f(xi) is F(x) = P(X≤x) =  , xR.

Cumulative Distribution Function from Probability Mass function

          Both the probability mass function and the cumulative distribution function of a discrete random variable X contain all the probabilistic information of X. The probability distribution of X is determined by either of them. In fact, the distribution function F of a discrete random variable X can be expressed in terms of the probability mass function f(x) of X and vice versa.

Example - If the probability mass function f (x) of a random variable X is

                           6.PNG

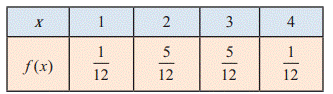
Find (i) its cumulative distribution function, hence find (ii) P (X ≤ 3) and, (iii) P (X ≥ 2)

Solution – P(X<1) = 0 for

                     F(1) = P(X≤1) = P(X<1) + P(X = 1) = 0 +  =

                    F(2) = P(X≤2) = P(X<1) + P(X = 1) + P(X = 2) =

                     F(3) = P(X<1) + P(X = 1) + P(X = 2) + P(X = 3) =

                     F(4) = P(X<1) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) =

Therefore the cumulative distribution function is

                                                            7.PNG

 

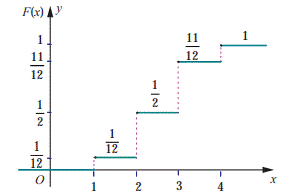
                  P(X≤3) = F(3) =

                  P(X≥2) = 1 – F(1) = 1 -

Probability Mass Function from Cumulative Distribution Function

Suppose X is a discrete random variable taking the values x1,x2,x3,---- such that x1<x2<x3<----  and F(xi) is the distribution function. Then the probability mass function f(xi)  is given by

Example -  A random variable X has the following probability mass function.

                          8.PNG

Find (i) P(2<X<6) (ii) P(2≤X<5) (iii) P(X≤4)  (iv) P (3<X)

Sol :              Since the given function is a probability mass function, the total probability is one. That is

                         k+2k+6k+5k+6k+10k =1

                          30k = 1

                            k =

Therefore the probability mass function is

                                         9.PNG

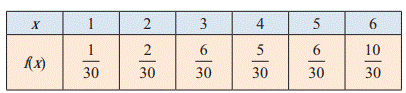
        (i) P(2<X<6) = f(3) +f(4) + f(5) =

         (ii) P(2≤X<5) = f(2) + f(3) +f(4) =

        (iii) P(X≤4)  = f(1) + f(2) + f(3) +f(4) =  =

        (iv) P (3<X) = f(4) + f(5) + f(6) =  +  =

 

Continuous Distributions

           Let S be a sample space and let a random variable X:SR that takes on any value in a set I of ℝ . Then X is called a continuous random variable if P(X=x) = 0 for every x in I.

Probability density function

A non-negative real valued function f (x) is said to be a probability density function if, for each possible outcome x, x  of a continuous random variable X having the property

       

10.PNG

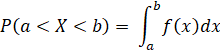
Distribution function (Cumulative distribution function)

The distribution function or cumulative distribution function F (x) of a continuous random variable X with probability density f(x) is

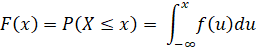
Distribution function from Probability density function

 Both the probability density function and the cumulative distribution function (or distribution function) of a continuous random variable X contain all the probabilistic information of X . The probability distribution of X is determined by either of them. Let us learn the method to determine the distribution function F of a continuous random variable X from the probability density function f (x) of X and vice versa.

Example -         If X is the random variable with probability density function f (x­) given by,

f(x) =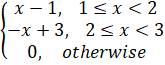                                                           

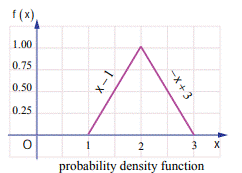
    11.PNG

       Find the distribution function F(x).

Sol:                                By definition,  F(x) = P(X ≤ x) =

                          When x<1,       F(x) = P(X ≤ x) =  = 0

                          When 1≤x<2,       F(x) = P(X ≤ x) =  +  =

                          When 2≤x<3   F(x) = P(X ≤ x) =  +  +  = 1-

                         When x≥ 3,  F(x) = P(X ≤ x) =  +  +  +   = 1

 

These give F(x) =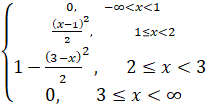

Probability density function from Probability distribution function

                Suppose F (x) is the distribution function of a continuous random variable X . Then the probability density function f (x­)is given by

                                                                                        when ever derivative exists.

Mathematical Expectation

              Suppose X is a random variable with probability mass (or) density function f (x)­. The expected value or mean or mathematical expectation of X , denoted by E (X) or μ is

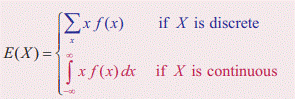
12.PNG

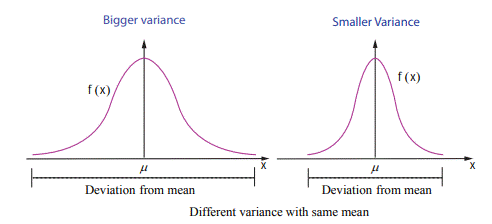
Variance

      The variance of a random variable X denoted by Var(X) or V(X) or ( or ) is

                  V(X) = E(X-E(X))2 = E(X - µ) 2

·         Square root of variance is called standard deviation.

Properties of Mathematical expectation and variance

              (i) E(aX+b) =  aE (X) + b ­ , where a and b are constants

Corollary 1: E (aX) = aE (X) (when b = 0 )

 Corollary 2: E (b) = b (when a = 0 )

               (ii) Var (X) ­ = E(X2) -  E(X)2

               (iii) Var(aX +b) = a2 Var(X) where a and b are constants

Corollary 3: V (aX) = a2 V (X) (when b = 0)

 Corollary 4: V (b) = 0 (when a = 0)

13.PNG

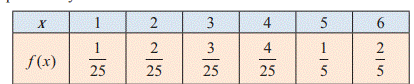
Example -       Suppose that f (x) given below represents a probability mass function,

                                                               14.PNG

Find (i) the value of c (ii) Mean and variance.

Sol:          (i)

              c2 + 2c2 + 3c2 + 4c2  + c + 2c = 1

             c =

Hence, the probability mass function is

                                                15.PNG                                                        

 

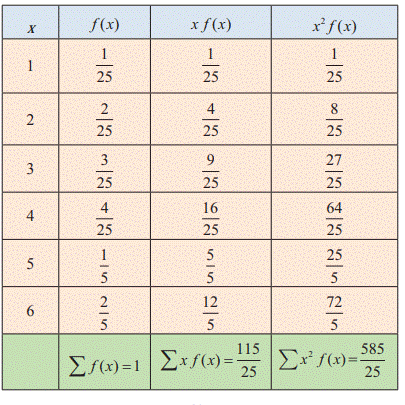
(ii) To find mean and variance, let us use the following table

                                                          16.PNG

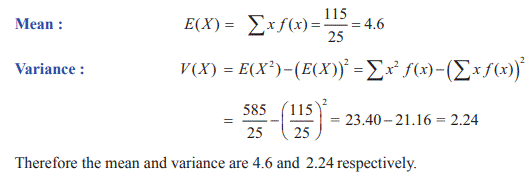
                                              17.PNG

Theoretical Distributions: Some Special Discrete Distributions                        

       The One point distribution

·        The random variable X has a one point distribution if there exists a point x0 such that, the probability mass function f (x) is defined as f (x) = P(X = x0) =1.

·        the mean and the variance are respectively x0 and 0 .

The Two point distribution

Unsymmetrical Case:  The random variable X has a two point distribution if there exists two values x1 and x2, such that

         

·        The mean and the variance are respectively px1  + qx2   and pq(x2 – x1)2

     Symmetrical Case: When p = q =

     The mean and variance respectively are  and

    The Bernoulli distribution

     Let X be a random variable associated with a Bernoulli trial by defining it as X (success) = 1 and X (failure) = 0, such that

       X is called a Bernoulli random variable and f (x) is called the Bernoulli distribution.

·        X is a Bernoulli’s random variable following with parameter p, the mean μ and variance σ2 of Bernoulli distribution are

                                                                                                  µ = p and

 

 The Binomial Distribution

                A discrete random variable X is called binomial random variable, if X is the number of successes in n -repeated trials such that

(i) The n- repeated trials are independent and n is finite

(ii) Each trial results only two possible outcomes, labelled as ‘success’ or ‘failure’

(iii) The probability of a success in each trial, denoted as p, remains constant.

  

·        The binomial random variable X, equals the number of successes with probability p for a success and q= 1- p ­for a failure in n-independent trials, has a binomial distribution denoted by X B(n, p). The probability mass function of X is

                       ,       x = 0,1,2, ………..

·        If X is a binomial random variable with parameters p and n, the mean μ and variance σ2 of binomial distribution are

                           µ = np  and

 

Example - Find the binomial distribution function for a fair die is rolled 10 times and X denotes the number of times 4 appeared.

Sol:       A fair die is rolled ten times and X denotes the number of times 4 appeared. X is binomial random variable that takes on the values 0,1,2,3,……,10 with n = 10 and p = .

             Probability of getting a four in a die is p =  and q = 1 – p = .

             Therefore the binomial distribution is