DISCRETE MATHEMATICS

Introduction

Continuous Mathematics - It is based upon the results concerning the set of real numbers which is uncountably infinite.

Discrete Mathematics - It involves distinct values which are either finite or countably infinite; i.e. between any two points, there are finite or countably infinite number of points.

· The mathematicians who lived in the latter part of the 19th and early in the 20th centuries developed a new branch of mathematics called discrete mathematics consisting of concepts based on either finite or countably infinite sets like the set of natural numbers.

· The main advantage of studying discrete mathematics is that its results serve as very good tools for improving the reasoning and problems solving capabilities.

· Some of the branches of discrete mathematics are combinatorics, mathematical logic, boolean algebra, graph theory, coding theory etc.

Symbols

- belongs to

- such that

- for every

- implies

- there exists

· In general, the word ‘operation’ refers to the process of operating upon either a single or more number of elements at a time.

· For instance, finding the negative of an element in Z involves a single¢For instance, finding the negative of an element in element at a time. So it is called an unary operation.

· On the other hand the process of finding the sum of any two elements in Z involves two elements at a time. This kind of operation is called a binary operation and in general an operation involving n elements is called an n-ary operation, n∈N.

Binary Operations

Definitions

· Any operation defined on a nonempty set is called a binary operation or a binary composition on the set in abstract algebra.

· Any operation * defined on a non-empty set S is called a binary operation on S if the following conditions are satisfied:

(i) The operation * must be defined for each and every ordered pair (a, b)∈ S X S.

(ii) It assigns a unique element a ∗ b of S to every ordered pair (a , b)∈ S X S.

· A binary operation defined by ∗: SXS → S; ∗(a, b) = a ∗ b ∈ S demands that the output a ∗ b must always lie the given set S and not in the complement of it. Then we say that ‘∗ is closed on S ’ or ‘ S is closed with respect to ∗ ’. This property is known as the closure property.

Algebraic structure - Any non-empty set on which one or more binary operations are defined is called an algebraic structure. Another way of defining a binary operation ∗ on S is as follows:

∀ a,b∈ S, a ∗b is unique and a ∗ b ∈ S .

Note –

· It follows that every binary operation satisfies the closure property.

· The operation∗ is just a symbol which may be +, ×, −, ÷ matrix addition, matrix multiplication, etc. depending on the set on which it is defined.

· For instance, though + and × are binary on N, - is not binary operation on N.

Operation	N	Z	Q	R	C	Q\{0}	R\{0}	C\{0}
+	Binary	Binary	Binary	Binary	Binary	Not Binary	Not Binary	Not Binary
-	Not Binary	Binary	Binary	Binary	Binary	Not Binary	Not Binary	Not Binary
X	Binary	Binary	Binary	Binary	Binary	Binary	Binary	Binary
	Not Binary	Not Binary	Not Binary	Not Binary	Not Binary	Binary	Binary	Binary

Example - Examine the binary operation (closure property) of the following operations on the respective sets (if it is not, make it binary):

(i) (ii)

Sol: (i) Since × is binary operation on Z, a,b Z ⇒a x b = abZ ------- (1)

The fact that + is binary operation on Z and (1) ⇒3ab = (ab +ab +ab) Z and (2)

Also a and 3ab -------------- (3)

(2),(3) yield a * b the closure property of - on Z yield a * b = . Since a * b is a binary operation on Z.

(ii) In this problem a ∗ b is in the quotient form. Since the division by 0 is undefined, the denominator b -1must be nonzero.

It is clear that b – 1 = 0 if b =1. As 1∈Q, * is not a binary operation on the whole of Q. However it can be found that by omitting 1 from Q, the output a ∗ b exists in Q\{1}.

Hence ∗ is a binary operation on Q\{1}.

Some more properties of a binary operation

Commutative property - Any binary operation ∗ defined on a nonempty set S is said to satisfy the commutative property, if

Associative property - Any binary operation ∗ defined on a nonempty set S is said to satisfy the associative property, if

Existence of identity property - An element e ∈ S is said to be the Identity Element of S under the binary operation∗ if for all a ∈ S we have that a ∗ e = a and e ∗ a = a .

Existence of inverse property - If an identity element e exists and if for every a ∈ S , there exists b in S such that a ∗ b = e and b ∗ a = e then b ∈ S is said to be the Inverse Element of a . In such instances, we write b = a^-1.

Note –

· a^-1 is an element of S. It should be read as the inverse of a and not as .

· The multiplicative identity is 1 in Z and it is the one and only one element with the property n.1 = 1.n = n, ∀ n ∈ Z

· The multiplicative inverse of any element, say 2 in Q is and no other nonzero rational number x has the property that 2.x = x.2 = 1.

Theorem: (Uniqueness of Identity)

· In an algebraic structure the identity element (if exists) must be unique.

Theorem: (Uniqueness of Inverse)

· In an algebraic structure the inverse of an element (if exists) must be unique.

Example - Verify the (i) closure property, (ii) commutative property, (iii) associative property (iv) existence of identity and (v) existence of inverse for the arithmetic operation – on Z.

Sol: (i) Though - is not binary on N, it is binary on Z. To check the validity of any more properties satisfied by – on Z, it is better to check them for some particular simple values. (ii) Take m = 4 , n = 5 and (m – n) = (4 – 5) = −1 and (n – m) =(5 – 4) = 1. Hence (m – n) ≠ (n – m). So the operation - is not commutative on Z.

(iii) In order to check the associative property, let us put m = 4,n = 5 and p = 7 in both (m – n) - p and m – (n – p) .

(m – n)− p = (4 – 5) − 7 = -8 -------(1)

m – (n−p) = 4 – (5 – 7) = 6 -------(2)

From (1) and (2), it follows that (m – n) - p ≠ m - (n – p).

Hence – is not associative on Z.

(iv)Identity does not exist.

(v) Inverse does not exist.

Some binary operations on Boolean Matrices

· A Boolean Matrix is a real matrix whose entries are either 0 or 1.

·

where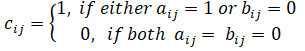

·

where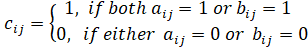

Properties satisfied by join and meet

Let 𝔹 be the set of all boolean matrices of the same type. We only state the properties of meet and join.

Closure property – A, B ∈𝔹, A V B = V = 𝔹.

Associative property - A ∨ (B ∨ C) = (A V B) V C, 𝔹. ∨ is associative.

Existence of identity property - ∀ A ∈ 𝔹, ∃ the null matrix 0∈𝔹⋺ A∨0 = 0∨A = 0. The identity element for ∨ is the null matrix.

Existence of inverse property - The inverse does not exist

Modular Arithmetic

The modular arithmetic refers to the process of dividing some number a by a positive integer (n > 1), called modulus, and then equating a with the remainder b modulo n and it is written as a ≡ b (mod n), read as ‘a is congruent to b modulo n .’

· The addition modulo n is defined as follows. Let a b ∈ Z_n. Then a +_n b = n the remainder of a + b on division by n.

· The multiplication modulo n is defined as follows. Let a, b ∈ Z_n. Then a ×_n b the remainder of a x b on division by n.

Mathematical Logic

The reputed Greek philosopher Aristotle (384-322BC(BCE))wrote the first book on logic. The famous German philosopher and mathematician Gottfried Leibnitz of 17^th century framed the idea of using symbols in Logic. Later this idea was realized by George Boole and Augustus de Morgan in 19^th century. George Boole established the fact that logic is very much related to mathematics by linking logic, symbols, and algebra together. Mathematical Logic was developed in the late 19^th and early 20^th centuries.

Statement and its truth value

The simplest part of Mathematical Logic is the Propositional Logic and its building blocks are statements or propositions. Mostly communication needs the use of language through which we impart our ideas. They are in the form of sentences. There are various types of sentences like

(1) Declarative (Assertive type)

(2) Imperative (A command or a request type)

(3) Exclamatory (Emotions, excitement type)

(4) Interrogative (Question type)

(5) Open type

· Any declarative sentence is called a statement or a proposition which is either true or false but not both.

· Any imperative sentence such as exclamatory, command and any interrogative sentence cannot be a proposition.

· The truth value of a statement refers to the truth or the falsity of that particular statement.

· The truth value of a true statement is true and it is denoted by T or 1.

· The truth value of a false statement is false and it is denoted by F or 0.

· An open sentence is a sentence whose truth can vary according to some conditions, which are not stated in the sentence.

Example - Identify the valid statements from the following sentences.

Solution: (1) Mount Everest is the highest mountain of the world.

(2) 3 4 + = 8

(3) 751 + > 0

(4) Give me that book

(5) (10 – x) = 7

(6) How beautiful this flower is!

(7) Where are you going?

(8) Wish you all success

(9) This is the beginning of the end

The truth value of the sentences (1) and (3) are T, while that of (2) is F. Hence they are statements. The sentence (5) is true for x = 3 and false for x ≠ 3 and hence it may be true or false but not both. So it is also a statement. The sentences (4),(6),(7),(8) are not statements, because (4)is a command,(6)is an exclamatory, (7) is a question while (8) is a sentence expressing one’s wishes and (9) is a paradox.

Compound Statements, Logical Connectives, and Truth Tables

· Any sentence which cannot be split further into two or more statements is called an atomic statement or a simple statement. If a statement is the combination of two or more simple statements, then it is called a compound statement or a molecular statement. Hence it is clear that any statement can be either a simple statement or a compound statement.

· To connect two or more simple sentences, we use the words or a group of words such as “and”, “or”, “if-then”, “if and only if”, and “not”. These connecting words are known as logical connectives.

· In order to construct a compound statement from simple statements, some connectives are used. Some basic logical connectives are negation (not), conjunction (and) and disjunction (or).

· A statement formula is an expression involving one or more statements connected by some logical connectives.

· A table showing the relationship between truth values of simple statements and the truth values of compound statements formed by using these simple statements is called truth table.

Logical Connectives and their Truth Tables

Truth Table for NOT [¬] (Negation)

p	¬ p
T	F
F	T

Truth table for AND [ ∧ ] (Conjunction)

p	q	p q
T	T	T
T	F	F
F	T	F
F	F	F

The truth tables for OR [∨ ] (Disjunction)

p	q	p V q
T	T	T
T	F	T
F	T	T
F	F	F

Conditional Statement

The conditional statement of any two statements p and q is the statement, “If p, then q” and it is denoted by p → q . Here p is called the hypothesis or antecedent and q is called the conclusion or consequence. p → q is false only if p is true and q is false. Otherwise it is true.

p	q	p q
T	T	T
T	F	F
F	T	T
F	F	T

Consequences

From the conditional statement p → q , three more conditional statements are derived. They are listed below.

(i) Converse statement q → p .

(ii) Inverse statement ¬ p→ ¬q.

(iii) Contrapositive statement ¬ q→ ¬p.

Bi-conditional Statement

The bi-conditional statement of any two statements p and q is the statement “ p if and only if q ” and is denoted by p ↔ q . Its truth value is T, whenever both p and q have the same truth values, otherwise it is false.

p	q	p ↔ q
T	T	T
T	F	F
F	T	F
F	F	T

Exclusive OR (EOR) [∨]

Let p and q be any two statements. Then p EOR q is such a compound statement that its truth value is decided by either p or q but not both. It is denoted by p ⊽ q. The truth value of p ⊽ q is T whenever either p or q is T, otherwise it is F. The truth table of p ⊽ q is given below.

p	q	p q
T	T	F
T	F	T
F	T	T
F	F	F

Exercise - Construct the truth table for.

Tautology, Contradiction, and Contingency

· A statement is said to be a tautology if its truth value is always T irrespective of the truth values of its component statements. It is denoted by 𝕋.

· A statement is said to be a contradiction if its truth value is always F irrespective of the truth values of its component statements. It is denoted by 𝔽.

· A statement which is neither a tautology nor a contradiction is called contingency.

Observations –

1. For a tautology, all the entries in the column corresponding to the statement formula will contain T.

2. For a contradiction, all the entries in the column corresponding to the statement formula will contain F.

3. The negation of a tautology is a contradiction and the negation of a contradiction is a tautology.

4. The disjunction of a statement with its negation is a tautology and the conjunction of a statement with its negation is a contradiction. That is p ∨¬p is a tautology and p ∧¬p is a contradiction. This can be easily seen by constructing their truth tables as given below.

Example for tautology –

p	¬p	p V ¬p
T	F	T
F	T	T

Example for contradiction –

p	¬p	p ∧ ¬p
T	F	F
F	T	F

Example for contingency –

p	q		¬q	p¬q	¬(p→ ¬q)	(p↔q) ∧ ¬ (p →¬q)
T	T	T	F	F	T	T
T	F	F	T	T	F	F
F	T	F	F	T	F	F
F	F	T	T	T	F	F

Duality –

The dual of a statement formula is obtained by replacing ∨ by ∧ , ∧ by ∨ , T by F, F by T . A dual is obtained by replacing 𝕋 (tautology) by 𝔽 (contradiction), and, 𝔽 by 𝕋.

Remarks –

(1) The symbol ¬ is not changed while finding the dual.

(2) Dual of a dual is the statement itself.

(3) The special statements 𝕋 (tautology) and 𝔽 (contradiction) are duals of each other.

(4) T is changed to F and vice-versa

Logical Equivalence –

Any two compound statements A and B are said to be logically equivalent or simply equivalent if the columns corresponding to A and B in the truth table have identical truth values. The logical equivalence of the statements A and B is denoted by A ≡ B or A ⇔ B.

Some Laws of Equivalence –

1. Idempotent Laws

(i) p ∨ p ≡ p (ii) p ∧ p ≡ p

2. Commutative Laws

(i) p ∨ q ≡ q ∨ p (ii) p ∧ q ≡ q ∧ p

3. Associative Laws

(i) p ∨ (q ∨ )r ≡ (p ∨ q) ∨ r (ii) p ∧(q ∧ r) ≡ (p ∧ q) ∧ r

4. Distributive Laws

(i) p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) (ii) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (P ∧ r)

5. Identity Laws

(i) p ∨ 𝕋 ≡𝕋 and p ∨ 𝔽 ≡ p (ii) p ∧ 𝕋≡ p and p ∧ 𝔽 ≡ 𝔽

6. Complement Laws

(i) p ∨ ¬p ≡ 𝕋 and p ∧ ¬p ≡ 𝔽 (ii) ¬𝕋 ≡ 𝔽 and ¬𝔽 ≡ 𝕋

7. Involution Law or Double Negation Law

¬(¬ p) ≡ p

8. de Morgan’s Laws

(i) ¬ (p ∧ q) = ¬p ∨ ¬q (ii) ¬(p ∨ q) ≡ ¬p ∧ ¬q

9. Absorption Laws

(i) p ∨ (p ∧ q) ≡ p (ii) p ∧ (p ∨ q) = p