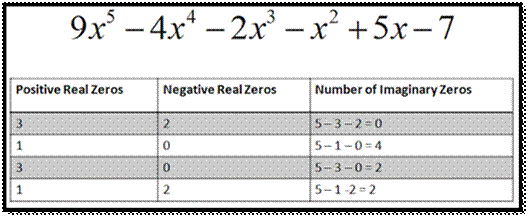Theory Of Equation

Introduction:

In algebra, the theory of equations is the study of algebraic equations (also called “polynomial equations”), which are equations defined by a polynomial. The main problem of the theory of equations was to know when an algebraic equation has an algebraic solution.

Equation of nth degree has a total ‘n’ real or imaginary roots. If α is the root of Equation f (x) = 0, then the polynomial f (x) is exactly divisible by (x – α) i.e. (x – α) is the factor of the given polynomial f (x).

Polynomial Equation:

The equations formed with variables, exponents and coefficients are called as polynomial equations. It can have a number of different exponents, where the higher one is called the degree of the equation. We can solve polynomials by factoring them in terms of degree and variables present in the equation.

A polynomial function is an equation which consists of a single independent variable, where the variable can occur in the equation more than one time with different degree of the exponent. Students will also learn here to solve these polynomial functions. The graph of a polynomial function can also be drawn using turning points, intercepts, end behavior and the Intermediate Value Theorem.

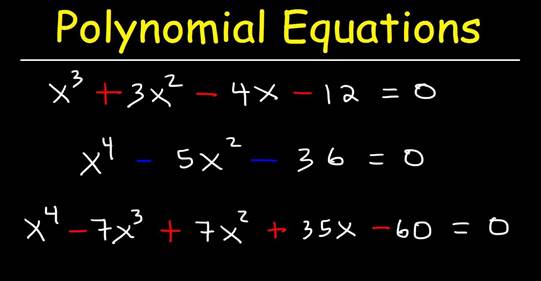
Example of polynomial function:

f(x) = 3x²+ 5x + 19

Polynomial	Example	Degree
Linear	2x+1	1
Quadratic	3x²+2x+1	2
Cubic	4x³+3x²+2x+1	3
Quartic	5x⁴+4x³+3x²+2 x+1	4

Vieta’s Formulae and Formation of Polynomial Equations

Vita’s Formula - Forming Quadratics :

x 2 + b x + c ≡ x 2 − ( p + q ) x + p q . x²+bx+c\x²-(p+q)x+pq. ...

This is the so-called Vita’s formula for a quadratic polynomial. It can be similarly extended to polynomials of higher degree.

In mathematics, Vieta’s formulas are formulas that relate the coefficients of a polynomial to sums and products of its roots. It was discovered by the Francois Viete. The most simplest application of Viete’s formula is quadratics and are used specifically in algebra.

Basic formula of Vieta’s in any general polynomial of degree n:

P(x)=anxn+an−1xn−1+….+a1x+a0

Equivalently stated, the (n−k)th coefficient an−k is related to a signed sum of all possible subproducts of roots, taken k at-a-time:

∑1≤i1<i2….ik≤nri1ri2….rik=(−1)kan−kan

for k = 1, 2, …, n (where we wrote the indices ik in increasing order to ensure each sub product of roots is used exactly once).

Applications Of Geometry :

Despite all of the different subject areas of mathematics that exist, perhaps geometry has the most profound impact on our everyday lives. Consider the environment you are in right now. Everything around you has a shape, volume, surface area, location, and other physical properties. Since its origins, geometry has significantly impacted the ways people live.

Common Applications of Geometry :

While we may not immediately think "geometry" when we perform everyday tasks, geometry is all around us. For instance, stop signs have the shape of an octagon, fish tanks must be carefully filled so as to prevent overflowing, and gifts need a certain amount of wrapping paper to look nice, just to name a few real-life applications. In this geometry section, you will learn many more applications of geometry that you can use on an everyday basis.

Advanced Applications Of Geometry :

As we find ourselves in a dynamic, technologically-driven society, geometry is becoming a subject of increasing importance. For example, molecular modeling is a growing field that requires an understanding of various arrangements of spheres as well as the ability to compute molecular properties like volume and topology. Architecture is another major application of geometry. The construction of a building and the structure of its components are important to consider in order to maximize building safety. Robot motion planning uses a subarea of computational geometry that focuses on the control of robot movement

NATURE OF ROOTS AND NATURE OF COEFFICIENTS OF POLYNOMIAL EQUATIONS :

The number of roots of a polynomial equation is equal to its degree. Hence, a quadratic equation has 2 roots. Let α and β be the roots of the general form of the quadratic equation : ax² + bx + c = 0. We can write:

α = (-b-√b²-4ac)/2a and

β = (-b+√b²-4ac)/2a

Here a, b, and c are real and rational. Hence, the nature of the roots α and β of equation ax² + bx + c = 0 depends on the quantity or expression (b² – 4ac) under the square root sign. We say this because the root of a negative number can’t be any real number. Say x² = -1 is a quadratic equation. There is no real number whose square is negative. Therefore for this equation, there are no real number solutions.

Hence, the expression (b² – 4ac) is called the discriminate of the quadratic equation ax² + bx + c = 0. Its value determines the nature of roots as we shall see. Depending on the values of the discriminate , we shall see some cases about the nature of roots of different quadratic equations.

Nature of roots	Discriminate	a>0a>0	a<0a<0
Roots are non-real	Δ<0Δ<0
Roots are real and equal	Δ=0Δ=0
Roots are real and unequal: · rational roots · irrational roots	Δ>0Δ>0 · Δ=Δ= squared rational · Δ=Δ= not squared rational

Roots of Higher Degree Polynomial Equations :

Factoring can also be applied to polynomials of higher degree, although the process of factoring is often a bit more laborious. Recall that a polynomial of degree n has n zeros, some of which may be the same (degenerate) or which may be complex. Consider the simple polynomial f(x) = x³; this polynomial can be factored as follows.

f(x) = (x)(x)(x)

As we can see from this expression, there are three zeros, all of which are at x = 0. Now, let's reverse our view of factoring a bit to illustrate the principle. Let's say we have a third-degree polynomial p(x) defined below.

p(x) = (x – 1)(x – 2)(x – 3) = (x² – 3x + 2)(x – 3) = x³ – 6x² + 11x – 6

Notice that we start with the factored form, which obviously has three zeros (one at x = 1, one at x = 2, and one at x = 3), and then use distributivity of multiplication to find the polynomial expression. Let's take a look at the graph of this function to confirm the location of the zeros.

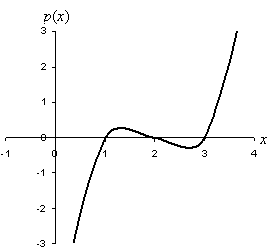
As we can see in the graph, the function crosses the x-axis at x = 1, x = 2, and x = 3. This confirms our assumption that the factored form elucidates the zeros of the function. As a result, we can construct a polynomial of degree n if we know all n zeros. Stated in another way, the n zeros of a polynomial of degree n completely determine that function. This same principle applies to polynomials of degree four and higher.

For example:

1. Add: 5x + 3y, 4x – 4y + z and -3x + 5y + 2z

First we need to write in the addition form.

Thus, the required addition

= (5x + 3y) + (4x – 4y + z) + (-3x + 5y + 2z)

= 5x + 3y + 4x – 4y + z - 3x + 5y + 2z

Now we need to arrange all the like terms and then all the like terms are added.

= 5x + 4x - 3x + 3y – 4y + 5y + z + 2z

= 6x + 4y + 3z

2. Add: 3a² + ab – b², -a² + 2ab + 3b² and 3a² – 10ab + 4b²

First we need to write in the addition form.

Thus, the required addition

                                            = (3a² + ab – b²) + (-a² + 2ab + 3b²) + (3a² – 10ab + 4b²)

                                             = 3a² + ab – b² - a² + 2ab + 3b² + 3a² – 10ab + 4b²

Here, we need to arrange the like terms and then add

                                               = 3a² - a² + 3a² + ab + 2ab – 10ab – b² + 3b² + 4b²

                                                  = 5a² – 7ab + 6b²

Descartes' rule of sign

Descartes' rule of sign is used to determine the number of real zeros of a polynomial function.

It tells us that the number of positive real zeroes in a polynomial function f(x) is the same or less than by an even numbers as the number of changes in the sign of the coefficients. The number of negative real zeroes of the f(x) is the same as the number of changes in sign of the coefficients of the terms of f(-x) or less than this by an even number.

Example

Determine the number of positive and negative real zeros for the given function (this example is also shown in our video lesson):

f(x)=x5+4x4−3x2+x−6f(x)=x5+4x4−3x2+x−6

Our function is arranged in descending powers of the variable, if it were not we would have to do that as a first step. Second we count the number of changes in sign for the coefficients of f(x).

Here are the coefficients of our variable in f(x):

1+4−3+1−61+4−3+1−6

Our variables goes from positive(1) to positive(4) to negative(-3) to positive(1) to negative(-6).

Between the first two coefficients there are no change in signs but between our second and third we have our first change, then between our third and fourth we have our second change and between our 4^th and 5^th coefficients we have a third change of coefficients. Descartes´ rule of signs tells us that the we then have exactly 3 real positive zeros or less but an odd number of zeros. Hence our number of positive zeros must then be either 3, or 1.

In order to find the number of negative zeros we find f(-x) and count the number of changes in sign for the coefficients:

f(−x) = (−x)5+4(−x)4−3(−x)2+(−x)−6

=−x5+4x4−3x2−x−6f(−x)

=(−x)5+4(−x)4−3(−x)2+(−x)−6

=−x5+4x4−3x2−x−6

Here we can see that we have two changes of signs, hence we have two negative zeros or less but a even number of zeros..

Totally we have 3 or 1 positive zeros or 2 or 0 negative zeros.