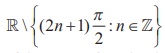Inverse Trigonomentric Function

Introduction:

Every mathematical function, from the simplest to the most complex, has an inverse. In mathematics, inverse usually means opposite. For addition, the inverse is subtraction. For multiplication, it's division. And for trigonometric functions, it's the inverse trigonometric functions.

Trigonometric functions are the functions of an angle. The term function is used to describe the relationship between two sets of numbers or variables. In modern mathematics, there are six basic trigonometric functions: sine, cosine, tangent, secant, cosecant, and cotangent. The inverse of these functions are inverse sine, inverse cosine, inverse tangent, inverse secant, inverse cosecant, and inverse cotangent.

Sine Function and Inverse Sine Function:

Inverse Sine function is a trigonometric function which expresses the inverse of the sine function and is represented as Sin^-1 or Arcsine. If sin 90 degrees is equal to 1, then the inverse of sin 1 or sin^-1 (1) equals to 90 degrees. Every trigonometric function, whether it is Sine, Cosine, Tangent, Cotangent, Secant or Cosecant has an inverse of it, though in a restricted domain.

Inverse Sine Function :

To understand the inverse of sine function out of other inverse trigonometric functions, we need to study Sine function first.

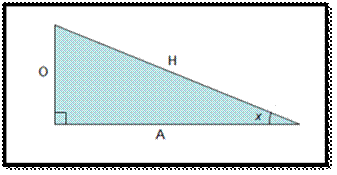
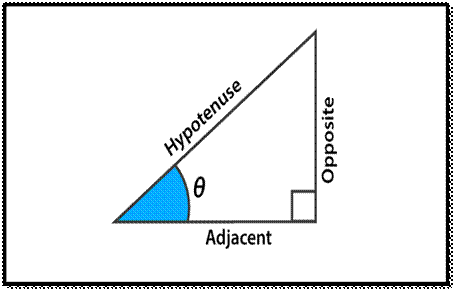
Sine Function: Sin (the sine function) takes an angle θ in a right-angled triangle and produces a ratio of the side opposite the angle θ to the hypotenuse.

Sin θ = Opposite / Hypotenuse

Inverse Sine:

The inverse of sine function or Sin^-1   takes the ratio, Opposite Side / Hypotenuse Side and produces angle θ. It is also written as arcsine or asine.

Sin inverse is denoted by sin^-1 or arcsin.

Example:

In a triangle, ABC, AB= 4.9m, BC=4.0 m, CA=2.8 m and angle B = 35°.

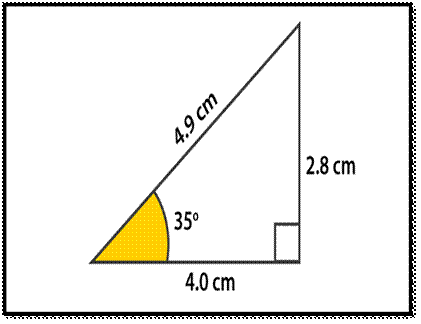
Solution:

• Sin 35° = Opposite / Hypotenuse
• Sin 35° = 2.8 / 4.9
• Sin 35° = 0.57°

So, Sin^-1 (Opposite / Hypotenuse) = 35°

Sin^-1 (0.57) = 35°

The Cosine Function and Inverse Cosine Function :

In a right-angled triangle, the cosine function is defined as the ratio of the length of base or adjacent side of the triangle(adjacent to angle) to that of the hypotenuse(the longest side) of the triangle. The Inverse Cosine function is the inverse of the Cosine function and is used to obtain the value of angles for a right-angled triangle.

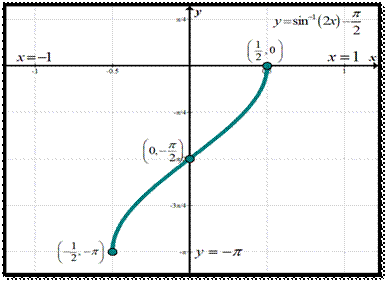
Inverse Cosine Function Graph :

The inverse of the cosine function is also called as “Arc Function” and is denoted as Arccos or Arccosine (acos). The graph of Arccosine function is given below;

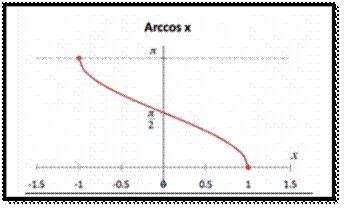
Where y=cos^-1 x(arccosine of x)

Also, the domain and range of arccosine function is denoted as;

Domain: −1 ≤ x ≤ 1

Range: 0 ≤ y ≤ π

Similarly, we can define other arc functions like;

Arcsine functions(inverse of sine function)

y = sin^-1 x

Arctangent function(inverse of tangent function)

y = tan^-1 x

Arccotangent function(inverse of cotangent function)

y = cot^-1 x

Arcsecant function(inverse of secant function)

y = sec^-1 x

And Arccosecant function(inverse of cosecant function)

y = cosec^-1 x

The Tangent Function and the Inverse Tangent Function :

Each of the trigonometric functions sine, cosine, tangent, secant, cosecant and cotangent has an inverse (with a restricted domain). The inverse is used to obtain the measure of an angle using the ratios from basic right triangle trigonometry. The inverse of tangent is denoted as Arctangent or on a calculator it will appear as atan or tan^-1.

Note: this does NOT mean tangent raised to the negative one power.

Example

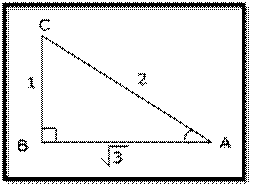
To find the measure in degrees of angle A using the tangent inverse, recall that 

Use a scientific calculator      *Make sure your calculator is in degree mode

30° = A

The Cosecant Function and the Inverse Cosecant Function:

When the length of the hypotenuse is divided by the length of the opposite side, it gives the Cosecant of an angle in a right triangle. It is denoted as Cosec, and the formula for Cosecant is:

The formula for Cosec x :

Cosec X = Hypotenuse/ OppositeSide

Cosecant is the reciprocal of Sin, Cosec x = 1SinX

Examples of Cosecant x Formula

Example 1: Find Cosec X if Sin x = 4/7

Solution: As Cosec X = 1/ Sin X

=1/4/7

=7/4

So, Cosec X = ⁷⁄₄

		Min	Max
	Re
	Im		5

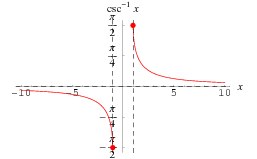
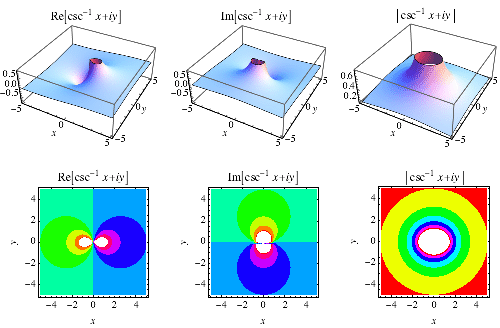
The principal value of the inverse cosecant

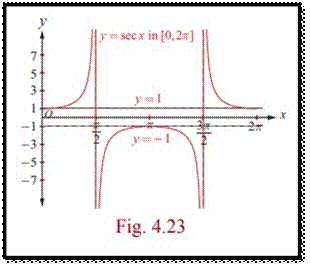
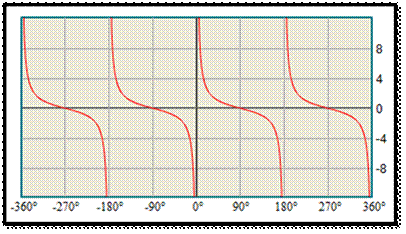
The secant function is defined as the reciprocal of cosine function. So, y = sec x=1/cosx is defined for all values of x except when cos x = 0 .Thus, the domain of the function y = sec x is  .

As −1 ≤ cos x ≤ 1, y = sec x does not take values in (−1, 1) . Thus, the range of the secant function is (−∞,1] ∪[1, ∞) . The secant function has neither maximum nor minimum. The function y = sec x is a periodic function with period 2π and it is also an even function.

The graph of the secant function :

The graph of secant function in 0 ≤ x ≤ 2 π,  x≠ π/2, 3π/2

The Cotangent Function and the Inverse Cotangent Function:

In a right triangle, the cotangent of an angle is the length of the adjacent side divided by the length of the opposite side. In a formula, it is abbreviated to just 'cot'.

Cot x=A/O

Of the six possible trigonometric functions, cotangent, secant, and cosecant, are rarely used. In fact, most calculators have no button for them, and software function libraries do not include them.

They can be easily replaced with derivations of the more common three: sin, cos and tan.
Cotangent can be derived in two ways:

Cot x=1/tan x

Cot x= cos X / Sin X

The Inverse cotangent fnction – arccot

For every trigonometry function such as cot, there is an inverse function that works in reverse. These inverse functions have the same name but with 'arc' in front. So the inverse of cot is arccot etc. When we see "arccot A", we interpret it as "the angle whose cotangent is A".

cot 60 = 0.577	Means: The cotangent of 60 degrees is 0.577
arccot 0.577 = 60	Means: The angle whose cotangent is 0.577 is 60 degrees.

Sometimes written as acot or cot^-1

Graph of the Cotangent function :

Because the cotangent function is the reciprocal of the tangent function, it goes to infinity whenever the tan function is zero and vice versa.

Principal Value of Inverse Trigonometric Functions:

The principal value of sin−1−1 x for x > 0, is the length of the arc of a unit circle centred at the origin which subtends an angle at the centre whose sine is x. For this reason sin^-1 x is also denoted by arc sin x. Similarly, cos−1−1 x, tan−1−1  x, csc−1−1  x, sec−1−1  x and cot−1−1 x are denoted by arc cos x, arc tan x, arc csc x, arc sec x.

1. Find the principal values of sin−1−1 (- 1/2)      

Solution: 

If θ be the principal value of sin−1−1 x then - π2π2 ≤ θ ≤ π2π2.

Therefore, If the principal value of sin−1−1 (- 1/2) be θ then sin−1−1 (- 1/2) = θ

⇒ sin θ = - 1/2 = sin (-π6π6) [Since, - π2π2 ≤ θ ≤ π2π2]

Therefore, the principal value of sin−1−1 (- 1/2) is (-π6π6).

2. Find the principal values of the inverse circular function cos−1−1 (- √3/2)

Solution:

 If the principal value of cos−1−1 x is θ then we know, 0 ≤ θ ≤ π.

Therefore, If the principal value of cos−1−1  (- √3/2) be θ then cos−1−1  (- √3/2) = θ

⇒ cos θ = (- √3/2) = cos π6π6 = cos (π - π6π6) [Since, 0 ≤ θ ≤ π]

Therefore, the principal value of cos−1−1  (- √3/2) is π - π6π6 = 5π65π6.

3. Find the principal values of the inverse trig function tan−1−1 (1/√3)

Solution:

If the principal value of tan−1−1 x is θ then we know, - π2π2 < θ < π2π2.

Therefore, If the principal value of tan−1−1 (1/√3) be θ then tan−1−1 (1/√3) = θ

⇒ tan θ = 1/√3 = tan π6π6 [Since, - π2π2 < θ < π2π2]

Therefore, the principal value of tan−1−1 (1/√3) is π6π6.

4. Find the principal values of the inverse circular function cot−1−1 (- 1)

Solution:

If the principal value of cot−1−1 x is α then we know, - π2π2 ≤ θ ≤ π2π2 and θ ≠ 0.

Therefore, If the principal value of cot−1−1 (- 1) be α then cot−1−1 (- 1) = θ

⇒ cot θ = (- 1) = cot (-π4π4) [Since, - π2π2 ≤ θ ≤ π2π2]  

Therefore, the principal value of cot−1−1 (- 1) is (-π4π4).    

5. Find the principal values of the inverse trig function sec−1−1 (1)

Solution:

If the principal value of sec−1−1 x is α then we know, 0 ≤ θ ≤ π and θ ≠ π2π2.

Therefore, If the principal value of sec−1−1 (1) be α then, sec−1−1 (1) = θ

⇒ sec θ = 1 = sec 0    [Since, 0 ≤ θ ≤ π]

Therefore, the principal value of sec−1−1 (1) is 0.

6. Find the principal values of the inverse trig function csc−1−1 (- 1).

Solution:

If the principal value of csc−1−1 x is α then we know, - π2π2 ≤ θ ≤ π2π2 and θ ≠ 0.

Therefore, if the principal value of csc−1−1 (- 1) be θ then csc−1−1 (- 1) = θ

⇒ csc θ = - 1 = csc (-π2π2) [Since, - π2π2 ≤ θ ≤ π2π2]

Therefore, the principal value of csc−1−1 (- 1) is (-π2π2).

There are a few inverse trigonometric functions properties which are crucial to not only solve problems but also to have a deeper understanding of this concept. To recall, inverse trigonometric functions are also called “Arc Functions,” since for a given value of a trigonometric function; they produce the length of arc needed to obtain that particular value. The range of an inverse function is defined as the range of values the inverse function can attain with the defined domain of the function. The domain of a function is defined as the set of every possible independent variable where the function exists. Inverse Trigonometric Functions are defined in a certain interval.

Considering the domain and range of the inverse functions, following formulas are important to be noted:

• sin(sin⁻¹x) = x, if -1 ≤ x ≤ 1
• cos(cos⁻¹x) = x, if -1 ≤ x ≤ 1
• tan(tan⁻¹x) = x, if -∞ ≤ x ≤∞
• cot(cot⁻¹x) = x, if -∞≤ x ≤∞
• sec(sec⁻¹x) = x, if -∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞
• cosec(cosec⁻¹x) = x, if -∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞

Property Set 1:

• Sin⁻¹(x) = cosec⁻¹(1/x), x∈ [−1,1]−{0}
• Cos⁻¹(x) = sec⁻¹(1/x), x ∈ [−1,1]−{0}
• Tan⁻¹(x) = cot⁻¹(1/x), if x > 0 Or,

= cot⁻¹⁽1/x) −π, if x < 0

• Cot⁻¹(x) = tan⁻¹(1/x), if x > 0 Or,

= tan⁻¹⁽1/x) + π, if x < 0

Property Set 2:

• Sin⁻¹(−x) = −Sin⁻¹(x)
• Tan⁻¹(−x) = −Tan⁻¹(x)
• Cos⁻¹(−x) = π − Cos⁻¹(x)
• Cosec⁻¹(−x) = − Cosec⁻¹(x)
• Sec⁻¹(−x) = π − Sec⁻¹(x)
• Cot⁻¹(−x) = π − Cot⁻¹(x)

Proofs:

1. Sin⁻¹⁽−x) = −Sin⁻¹(x)

Let sin⁻¹⁽−x) = y, i.e.,−x = sin y

⇒ x = − sin y

Thus,

x = sin (− y)

Or,

sin⁻¹(x) = −y = −sin⁻¹⁽−x)

Therefore, sin⁻¹⁽−x) = −sin⁻¹(x)

Similarly, using the same concept following results can be obtained:

• cosec⁻¹(−x) = −cosec⁻¹x, |x|≥1
• tan⁻¹(−x) = −tan⁻¹x, xϵR

2. Cos⁻¹⁽−x) = π − Cos⁻¹(x)

Let cos⁻¹⁽−x) = y i.e., −x = cos y

⇒ x = −cos y = cos(π–y)

Thus,

cos⁻¹(x) = π–y

Or,

cos⁻¹(x) = π–cos⁻¹⁽−x)

Therefore, cos⁻¹⁽−x) = π–cos⁻¹(x)

Similarly using the same concept following results can be obtained:

• sec⁻¹(−x) = π–sec⁻¹x, |x|≥1
• cot⁻¹(−x) = π–cot⁻¹x, xϵR

Property Set 3:

• Sin⁻¹(1/x) = cosec⁻¹x, x≥1 or x≤−1
• Cos⁻¹(1/x) = sec⁻¹x, x≥1 or x≤−1
• Tan⁻¹(1/x) = −π + cot⁻¹(x)

Proof:

Sin⁻¹⁽1/x) = cosec⁻¹x, x≥1 or x≤−1

Let cosec⁻¹ x = y, i.e. x = cosec y

⇒ (1/x) = sin y

Thus, sin⁻¹⁽1/x) = y

Or,

sin⁻¹⁽1/x) = cosec⁻¹x

Similarly using the same concept the other results can be obtained.

Illustrations:

• sin⁻¹(⅓) = cosec⁻¹(3)
• cos⁻¹(¼) = sec⁻¹(4)
• sin⁻¹(−¾) = cosec⁻¹(−4/3) = sin⁻¹(3/4)
• tan⁻¹(−3) = cot⁻¹(−⅓)−π

Property Set 4:

• Sin⁻¹(cos θ) = π/2 − θ, if θ∈[0,π]
• Cos⁻¹(sin θ) = π/2 − θ, if θ∈[−π/2, π/2]
• Tan⁻¹(cot θ) = π/2 − θ, θ∈[0,π]
• Cot⁻¹(tan θ) = π/2 − θ, θ∈[−π/2, π/2]
• Sec⁻¹(cosec θ) = π/2 − θ, θ∈[−π/2, 0]∪[0, π/2]
• Cosec⁻¹(sec θ) = π/2 − θ, θ∈[0,π]−{π/2}
• Sin⁻¹(x) = cos⁻¹[√(1−x²)], 0≤x≤1

= −cos^−1[√(1−x²)], −1≤x<0

Illustrations:

1. Given, cos⁻¹⁽−3/4) = π − sin⁻¹A. Find A.

Solution:

Draw the diagram from the question statement.

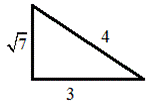
So,

cos⁻¹⁽−3/4) = π − sin⁻¹(√7/4)

Thus, A = √7/4

2. cos⁻¹⁽¼) = sin⁻¹ √(1−1/16) = sin⁻¹(√15/4)

3. sin⁻¹⁽−½) = −cos⁻¹√(1−¼) = −cos⁻¹(√3/2)

4. sin²(tan⁻¹(¾)) = sin²(sin⁻¹(⅗)) = (⅗)² = 9/25.

5. sin⁻¹⁽sin 2π/3) = π/3

6. cos⁻¹⁽cos 4π/3) = 2π/3

7. sin⁻¹⁽cos 33π/10) = sin⁻¹cos(3π + 3π/10) = sin⁻¹(−sin(π/2 − 3π/10)) = −(π/2 − 3π/10) = −π/5

Property Set 5:

• Sin⁻¹x + Cos⁻¹x = π/2
• Tan⁻¹x + Cot⁻¹(x) = π/2
• Sec⁻¹x + Cosec⁻¹x = π/2
• Tan⁻¹x + Tan⁻¹(1/x) = π/2, x>0

= −π/2, x<0

Proof:

sin⁻¹(x) + cos⁻¹(x) = (π/2), xϵ[−1,1]

Let sin⁻¹(x) = y, i.e., x = sin y = cos((π/2) − y)

⇒ cos⁻¹(x) = (π/2) – y = (π/2) − sin⁻¹(x)

Thus,

sin⁻¹(x) + cos⁻¹(x) = (π/2)

Similarly using the same concept following results can be obtained:

• tan⁻¹(x) + cot⁻¹(x) = (π/2), xϵR
• cosec⁻¹(x) + sec⁻¹(x) = (π/2), |x|≥1