Two Dimensional
Analytical Geometry
Introduction
Analytic geometry is that branch of Algebra in which the position of the
point on the plane can be located using an ordered pair of numbers called as
Coordinates. This is also called coordinate geometry or the cartesian geometry.
Analytic geometry is a contradiction to the synthetic geometry,
where there is no use of coordinates or formulas. It is considered axiom or assumptions,
to solve the problems. But in analytic geometry, it defines the
geometrical objects using the local coordinates. It also uses algebra to define
this geometry.
Coordinate geometry has its use in both two dimensional and
three-dimensional geometry. It is used to represent geometrical shapes. Let us
learn the terminologies used in analytic geometry, such as;
Plane
Coordinates
Planes
To understand how analytic geometry is important and useful,
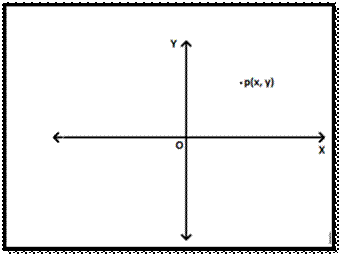
First, We need to learn what a plane is? If a flat surface goes on infinitely
in both the directions, it is called a Plane. So, if you find any
point on this plane, it is easy to locate it using Analytic Geometry. You
just need to know the coordinates of the point in X and Y plane.
Coordinates
Coordinates are the two ordered pair, which defines the location
of any given point in a plane.
CIRCLE
` In Maths or
in Geometry a circle is a special kind of ellipse in which the
eccentricity is zero and the two foci are coincident. A circle is also termed
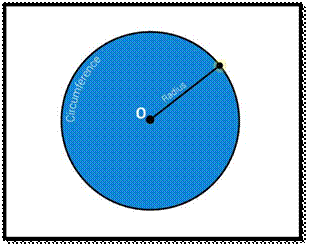
as the locus of the points drawn at an equidistant from the centre. The
distance from the center of the circle to the outer line is its radius.
Diameter is the line which divides the circle into two equal parts and is also
equal to twice of the radius.
A circle is a closed two-dimensional
figure in which the set of all the points in the plane is equidistant from a
given point called “centre”. Every line that passes through the circle forms
the line of reflection symmetry. Also, it has rotational symmetry around the
centre for every angle. The circle formula in the plane is given as:
(x-h)2 +
(y-k)2 = r2
where (x,y) are
the coordinate points
(h,k) is the coordinate of the centre of a
circle
and r is the radius of a circle.
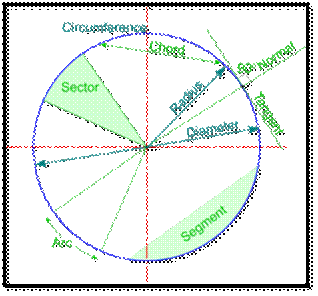
Circles Terminologies
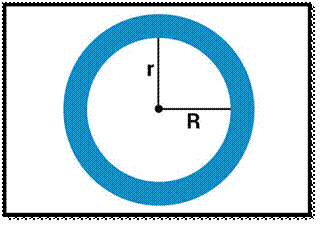
- Annulus-The region bounded by two concentric circles.
It is basically a ring-shaped object. See the figure below.
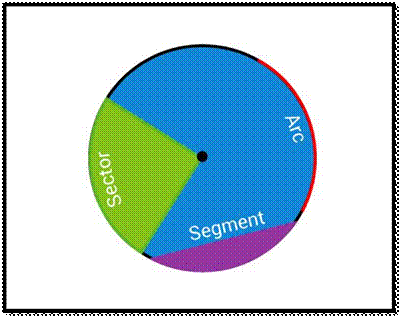
Arc – It is basically the connected
curve of a circle
Sector – A region bounded by two radii
and an arc.
Segment- A region bounded by a chord and
an arc lying between the chord’s endpoints. It is to be noted that segments do
not contain the centre.
·
·
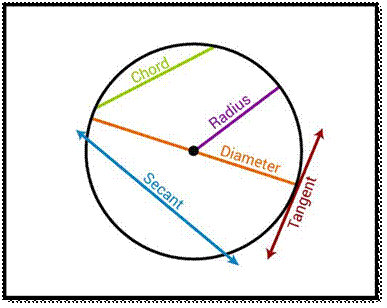
Centre – It is the midpoint of a circle.
Chord- A line segment whose endpoints lie on the circle
Diameter- A line segment having both the
endpoints on the circle
Radius- A line segment connecting the centre of a circle to any
point on the circle itself.
Secant- A straight line cutting the
circle at two points. It is also called as an extended chord.
Tangent- A coplanar straight line touching the circle at a single point.
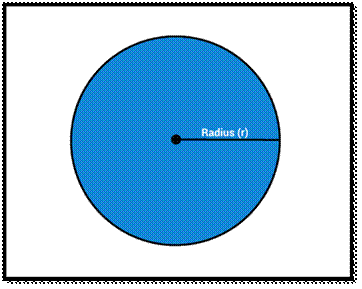
Radius of Circle (r)
A line segment connecting the centre
of a circle to any point on the circle itself “. The radius of
the circle is denoted by “R” or “r”.
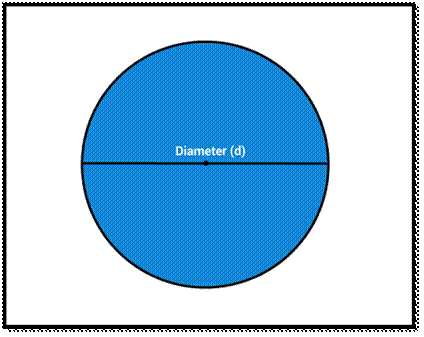
Diameter (d) of Circle
A line segment having both the
endpoints on the circle. It is twice the length of radius i.e. d = 2r. From
the diameter, the radius of the circle formula is obtained as r= d/2.
CONIC
conic
is the intersection of a plane and a right circular cone. The four basic types
of conics are parabolas, ellipses, circles, and hyperbolas. We've already
discussed parabolas and circles in previous sections, but here we'll define
them a new way. Study the figures below to see how a conic is geometrically
defined.
The conics above, the plane does not
pass through the vertex of the cone. When the plane does intersect the vertex
of the cone, the resulting conic is called a degenerate conic. Degenerate conics
include a point, a line, and two intersecting lines.
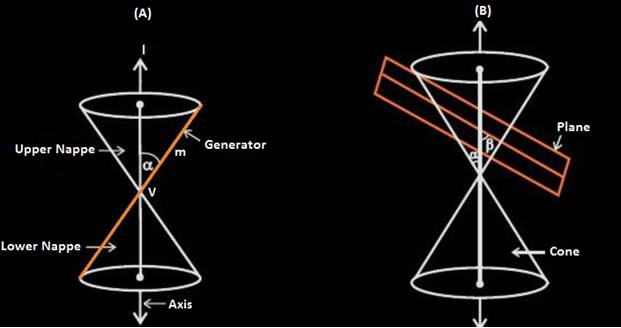
Conic Section
Conic sections are one of the important topics
in Geometry. It is basically a curve, generated by intersecting a right
circular cone with a plane. It is simply termed as ‘conic’. It has
distinguished properties in Euclidean geometry. The vertex of the cone divides
it into two nappes referred to as the upper nappe and the lower nappe.
In figure B, the cone is
intersected by a plane and the section so obtained is known as a conic section.
Depending upon the position of the plane which intersects the cone and the
angle of intersection β, different kind of conic sections are obtained.
Namely;
Circle
Ellipse
Parabola
Hyperbola
Conic Section Formulas
|
Circle |
(x−a)2+(y−b)2=r2(x−a)2+(y−b)2=r2 |
Center is (a,b) Radius is r |
|
Ellipse with horizontal major axis |
(x−a)2/h2+(y−b)2/k2=1 |
Center is (a, b) |
|
Ellipse with vertical major axis |
(x−a)2/k2+(y−b)2/h2=1 |
Center is (a, b) |
|
Hyperbola with horizontal transverse axis |
(x−a)2/h2−(y−b)2/k2=1 |
Center is (a,b) |
|
Hyperbola with vertical transverse axis |
(x−a)2/k2−(y−b)2/h2=1 |
Center is (a,b) |
|
Parabola with horizontal axis |
(y−b)2=4p(x−a), p≠0 |
Vertex is (a,b) |
|
Parabola with vertical axis |
(x−a)2=4p(y−b), p≠0 |
Vertex is (a,b) |
Sections of the Cone
Consider a fixed vertical line ‘l’ and another
line ‘m’ inclined at an angle ‘α’ intersecting ‘l’ at point V as shown
below:
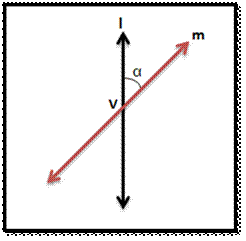
The initials as mentioned in the above figure A carry the
following meanings:
V is the vertex of the cone
l is the axis of the cone
m, the rotating line the is a generator of the cone
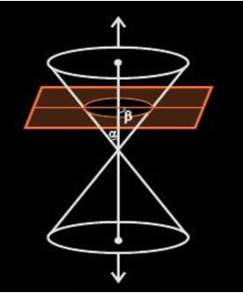
Conic Section Circle
If β=90o, the conic section formed is a circle
as shown below.
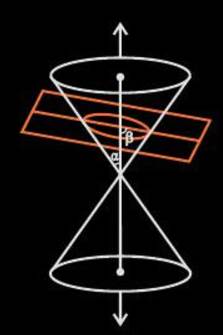
Conic Section Ellipse
If α<β<90o, the conic section so
formed is an ellipse as shown in the figure below.
Conic Section Parabola
If α=β, the conic section formed is a parabola
(represented by the orange curve) as shown below.
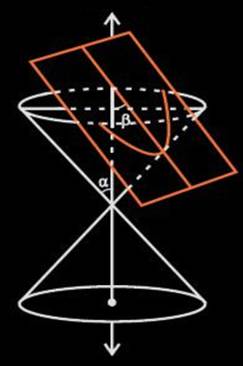
Conic Section Hyperbola
If 0≤β<α, then the plane intersects both
nappes and conic section so formed is known as a hyperbola (represented by the
orange curves).
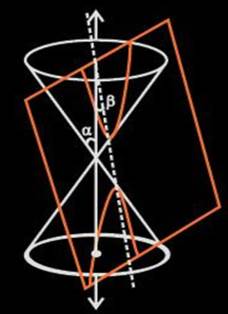
Parametric form of Conics
Apart from focus, eccentricity and directrix,
there are few more parameters defined under conic sections.
Principal Axis: Line joining the two focal
points or foci of ellipse or hyperbola. Its midpoint is the centre of the
curve.
Linear Eccentricity: Distance between the focus and
centre of a section.
Latus Rectum: A chord of section parallel to directrix, which passes through a focus.
Focal Parameter: Distance from focus to the
corresponding directrix
Major axis: Chord joining the two vertices.
It is the longest chord of an ellipse.
Minor axis: Shortest chord of an ellipse
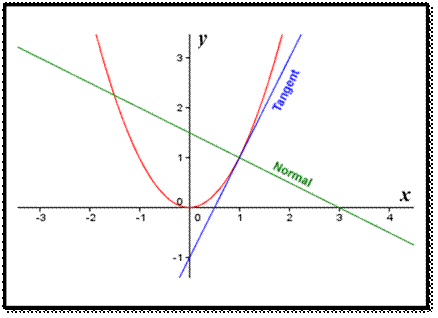
Tangents and Normal’s to Conics :
Tangents and Normals to Conics. Tangent to
a plane curve is a straight line touching the curve at exactly one point and a
straight line perpendicular to the tangent and passing through
the point of contact is called the normal at that point.
Real life Applications of Conics
:
Euclid and Archimedes are just two of the ancient Greek mathematicians to have
studied conic sections—the shapes created by slicing through a
double cone with a flat plane. If the plane is perpendicular to the axis of the
double cone, the intersection is a circle, and if the plane is angled parallel
to the side of the cone the intersection is a parabola. If the plane cuts
through both cones the intersection is a hyperbola. The only remaining case
gives an ellipse.
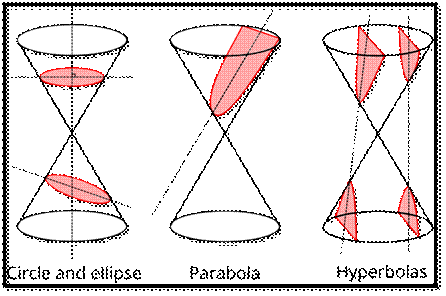
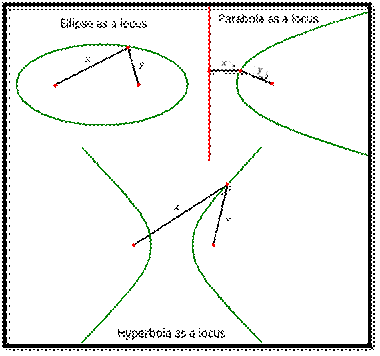
As well as having a description in terms of slicing through a
cone, these shapes also have a description in terms of loci (locations)
of points. A circle is the locus of points that are the same distance from the
centre (the focus of the circle). An ellipse is the locus of points whose
distances from two foci sum to a constant cc (that is, x+y=cx+y=c in the image
below). A hyperbola is the locus of points that have the same
difference cc between distances from two foci (that
is, |x−y|=c|x−y|=c). A parabola is the locus of points
equidistant from a focus and a straight line called the directrix
(that is, x=yx=y).
