TWO
DIMENSIONAL ANALYTICAL GEOMETRY-II
Introduction:
We are familiar with the concept of vectors, (vectus in
Latin means to carry) from our XI standard text book. Further the modern
version of Theory of Vectors arises from the ideas of Wessel(1745-1818)
and Argand (1768-1822) when they attempt to describe the complex numbers
geometrically as a directed line segment in a coordinate plane. We have seen
that a vector has magnitude and direction and two vectors with same magnitude
and direction regardless of positions of their initial points are always equal.
We also have studied addition of two vectors, scalar
multiplication of vectors, dot product, and cross product by denoting an
arbitrary vector by the notation ![]() or a1i +
a2j + a3k.
or a1i +
a2j + a3k.
.
The vector algebra has a few direct applications in physics and
it has a lot of applications along with vector calculus in physics,
engineering, and medicine. Some of them are mentioned below.
![]() To calculate the volume of a parallelepiped, the scalar triple product
is used.
To calculate the volume of a parallelepiped, the scalar triple product
is used.
![]() To find the work done and torque in mechanics, the dot and cross
products are respectiveluy used.
To find the work done and torque in mechanics, the dot and cross
products are respectiveluy used.
![]() To introduce curl and divergence of vectors, vector algebra is
used along with calculus. Curl and divergence are very much used in the study of
electromagnetism, hydrodynamics, blood flow, rocket launching, and the path of
a satellite.
To introduce curl and divergence of vectors, vector algebra is
used along with calculus. Curl and divergence are very much used in the study of
electromagnetism, hydrodynamics, blood flow, rocket launching, and the path of
a satellite.
Geometric Introduction To Vectors :
A vector ![]() is represented as a
directed straight line segment in a 3-dimensional space R3 ,
with an initial point A = (a1, a2, a3) ∈ R3 and
an end point B = (b1, b2, b3 )∈ R3 ,
and it is denoted by
is represented as a
directed straight line segment in a 3-dimensional space R3 ,
with an initial point A = (a1, a2, a3) ∈ R3 and
an end point B = (b1, b2, b3 )∈ R3 ,
and it is denoted by ![]() . The length of the line segment AB is the
magnitude of the vector
. The length of the line segment AB is the
magnitude of the vector ![]() and the direction
from A to B is the direction of the vector
and the direction
from A to B is the direction of the vector ![]() .
.
Hereafter, a vector will be interchangeably denoted
by ![]() or
or ![]() . Two vectors
. Two vectors ![]() and
and ![]() in R3 are said to be equal if
and only if the length AB is equal to the length CD and
the direction from A to B is parallel to the
direction from C to D . If
in R3 are said to be equal if
and only if the length AB is equal to the length CD and
the direction from A to B is parallel to the
direction from C to D . If ![]() and
and ![]() are equal, we write
are equal, we write ![]() =
= ![]() , and
, and ![]() is called a translate of
is called a translate of ![]() .
.
Given a vector ![]() ,
the length of the vector |
,
the length of the vector |![]() | is calculated by
| is calculated by
![]()
where A is (a1 , a2 , a3 )
and B is (b1 , b2 , b3 ).
In particular, if a vector is the position vector ![]() of (b1 , b2 , b3 ),
then its length is
of (b1 , b2 , b3 ),
then its length is
![]()
A vector having length 1 is called a unit vector. We the notation u , for a unit vector. Note that i,
j , and k use are unit
vectors and ![]() is the unique vector with length 0 . The direction
of
is the unique vector with length 0 . The direction
of ![]() is specified according to the context.
is specified according to the context.
The addition and scalar multiplication on vectors in 3-dimensional space are defined by
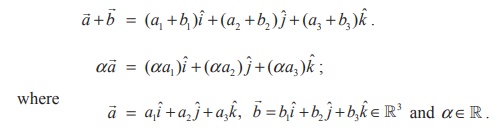
To see the geometric interpretation of ![]() +
+ ![]() , let
, let ![]() and
and ![]() , denote the position vectors of A = (a1 , a2 , a3 )
and B = (b1 , b2 , b3 )
, respectively. Translate the position vector
, denote the position vectors of A = (a1 , a2 , a3 )
and B = (b1 , b2 , b3 )
, respectively. Translate the position vector ![]() to the vector with initial point as A and
end point as C = (c1 , c2 , c3 )
, for a suitable (c1 , c2 , c3 ) ∈ R3.
See the Fig (6.2). Then, the position vector
to the vector with initial point as A and
end point as C = (c1 , c2 , c3 )
, for a suitable (c1 , c2 , c3 ) ∈ R3.
See the Fig (6.2). Then, the position vector ![]() of the point (c1 , c2 , c3 )
is equal to
of the point (c1 , c2 , c3 )
is equal to ![]() +
+ ![]() .
.
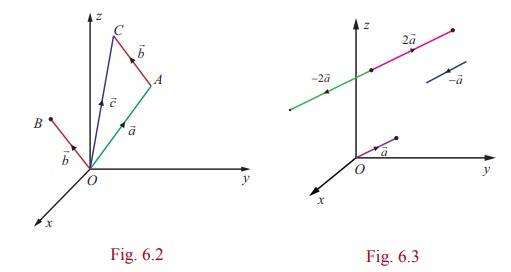
The vector α![]() is another vector parallel
to
is another vector parallel
to ![]() and its length is magnified
(if α > 1) or contracted (if
0 < α < 1) . If α < 0 , then α
and its length is magnified
(if α > 1) or contracted (if
0 < α < 1) . If α < 0 , then α ![]() is a vector whose magnitude
is | α | times that of
is a vector whose magnitude
is | α | times that of ![]() and direction opposite to
that of
and direction opposite to
that of ![]() . In particular, if α = −1, then α
. In particular, if α = −1, then α![]() = −
= −![]() is the vector with same length and direction opposite to that of
is the vector with same length and direction opposite to that of ![]() .
See Fig. 6.3
.
See Fig. 6.3
Scalar Product And Vector Product :
The Scalar Product And Vector Product
Of Two Vectors As Follows.
1 . Geometrical
interpretation
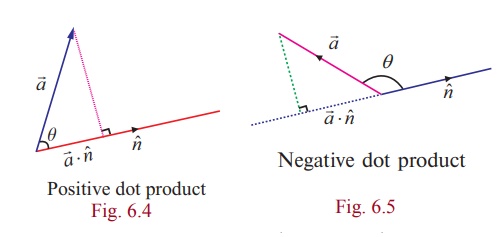
Geometrically, if ![]() is an arbitrary vector
and n is a unit vector, then
is an arbitrary vector
and n is a unit vector, then ![]() ⋅ n is the
projection of the vector
⋅ n is the
projection of the vector ![]() on the straight line on
which n lies. The quantity
on the straight line on
which n lies. The quantity ![]() ⋅ n is positive if the angle between
⋅ n is positive if the angle between ![]() and n is
acute, see Fig. 6.4 and negative if the angle between
and n is
acute, see Fig. 6.4 and negative if the angle between ![]() and n is
obtuse see Fig. 6.5.
and n is
obtuse see Fig. 6.5.
If ![]() and
and ![]() are arbitrary non-zero vectors, then |
are arbitrary non-zero vectors, then | ![]()
![]() | =
| =  and so |
and so | ![]()
![]() | means either the length of the straight line segment
obtained by projecting the vector |
| means either the length of the straight line segment
obtained by projecting the vector | ![]() |
| ![]() along the direction of
along the direction of ![]() or the length of the line segment obtained by
projecting the vector |
or the length of the line segment obtained by
projecting the vector | ![]() |
| ![]() along the direction
of
along the direction
of ![]() . We recall that
. We recall that ![]()
![]() =|
=| ![]() | |
| | ![]() | cosθ , where θ is the angle between the two vectors
| cosθ , where θ is the angle between the two vectors ![]() and
and ![]() . We recall that the angle
between
. We recall that the angle
between ![]() and
and ![]() is defined as the measure from
is defined as the measure from ![]() to
to ![]() in the counter clockwise direction.
in the counter clockwise direction.
The vector ![]()
![]() is either
is either ![]() or a vector perpendicular to the plane parallel to
both
or a vector perpendicular to the plane parallel to
both ![]() and
and ![]() having magnitude as the
area of the parallelogram formed by coterminus
vectors parallel to
having magnitude as the
area of the parallelogram formed by coterminus
vectors parallel to ![]() and
and ![]() .
If
.
If ![]() and
and ![]() are non-zero vectors, then the magnitude of
are non-zero vectors, then the magnitude of ![]() b can be calculated
by the formula
b can be calculated
by the formula
| ![]()
![]() | = | a | | b | | sinθ |,
where θ is the angle between
| = | a | | b | | sinθ |,
where θ is the angle between ![]() and
and ![]() .
.
Two vectors are said to be coterminus if
they have same initial point.
2. Application Of Dot And Cross Products In Plane Trigonometry :
We apply the concepts of dot and cross products of two vectors
to derive a few formulae in plane trigonometry.
1. (Cosine formulae)
With usual notations, in any triangle ABC, prove
the following by vector method.
![]() a2 = b2 + c2 - 2bc cos A
a2 = b2 + c2 - 2bc cos A
![]() b2 = c2 + a2 - 2ca cos B
b2 = c2 + a2 - 2ca cos B
![]() c2 = a2 + b2 - 2ab cos C
c2 = a2 + b2 - 2ab cos C
Solution
With usual notations in triangle ABC, we have

a2 = b2 + c2 + 2bc cos(π
- A)
a2 = b2 + c2 - 2bc cos A .
The results in (ii) and (iii) are proved in a similar way.
2. With usual notations, in any triangle ABC, prove the
following by vector method.
(i) a = b cos C + c cos B
(i) b = c cos A + a cos C
(iii) c = a cos B + b cos A
Solution :
With usual notations in triangle ABC, we have ![]() = a,
= a, ![]() =
= ![]() , and
, and

⇒ a2 = ab cos C + ac cos B
Therefore a = b cos C + c cos B . The results in (ii) and (iii) are proved in
a similar way.
3.
By vector method, prove that cos(α + β ) = cosα cos β −
sin α sin β .
Solution
Let a = ![]() and b
=
and b
= ![]() be
the unit vectors and which make angles α and β ,
respectively, with positive x -axis,
where A and B are as in the Fig. 6.8. Draw AL and BM perpendicular
to the x-axis.
be
the unit vectors and which make angles α and β ,
respectively, with positive x -axis,
where A and B are as in the Fig. 6.8. Draw AL and BM perpendicular
to the x-axis.

On
the other hand, from (1) and (2)
a ⋅ b =
(cosαi − sin α j) ⋅ (cos β i + sin βj) = cosα cos β −
sin α sin β----------------------------(4)
From
(3) and (4),
we get cos(α + β )
= cosα cos β − sin α sin β.
4.
Prove by vector method
that sin(α − β )
= sin α cos β − cosα sin β .
Solution
Let a = ![]() and
and ![]() =
= ![]() be the unit vectors
making angles α
and β respectively, with positive x -axis,
where A and B are as shown in
the Fig. 6.10. Then, we get a =
cosαi + sin α j and b
= cos β i + sin β j ,
be the unit vectors
making angles α
and β respectively, with positive x -axis,
where A and B are as shown in
the Fig. 6.10. Then, we get a =
cosαi + sin α j and b
= cos β i + sin β j ,
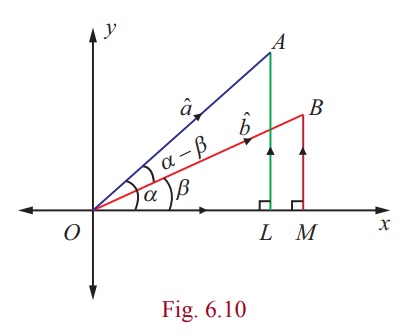
The angle between a and b is α − β and,
the vectors b, a, k
form a right-handed system.
Hence, we get
a Χ b | b | |
a | sin(α - β )k = sin(α - β
)k
(1)
On the other hand,
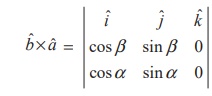 = (sin α cos β - cosα sin β )k ... (2)
= (sin α cos β - cosα sin β )k ... (2)
Hence, equations (1) and (2), leads to
sin(α - β ) = sin
α cos β - cosα sin β .
3. Application of dot and cross products in Geometry
:
1. (Apollonius theorem)
If D is the midpoint of the side BC of
a triangle ABC, show by vector method that
![]()
Solution
Let A be the origin, ![]() be the position vector
of B and
be the position vector
of B and ![]() be the position vector
of C. Now D is the midpoint of BC , and so the, position vector of D
is
be the position vector
of C. Now D is the midpoint of BC , and so the, position vector of D
is ![]()
Therefore , we have


Scalar
triple product
1
.For a given set of three vectors ![]() ,
, ![]() ,
and
,
and ![]() ,
the scalar (
,
the scalar (![]() Χ
Χ ![]() ) ⋅
) ⋅ ![]() is called a scalar
triple product of
is called a scalar
triple product of ![]() ,
, ![]() ,
, ![]() .
.
Given
any three vectors ![]() ,
, ![]() ,
, ![]() and
c the following are scalar triple products:
and
c the following are scalar triple products:
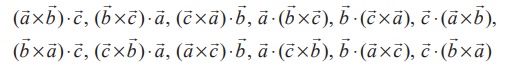
Geometrical
interpretation of scalar triple product :
Geometrically,
the absolute value of the scalar triple product ( ![]() Χ
Χ ![]() ) .
) .![]() . is
the volume of the parallelepiped formed by using the three vectors
. is
the volume of the parallelepiped formed by using the three vectors ![]() ,
, ![]() and
and ![]() as
co-terminus edges. Indeed, the magnitude of the vector (
as
co-terminus edges. Indeed, the magnitude of the vector (![]() Χ
Χ ![]() )
is the area of the parallelogram formed by using
)
is the area of the parallelogram formed by using ![]() and
and ![]() ;
and the direction of the vector (
;
and the direction of the vector (![]() Χ
Χ ![]() )
is perpendicular to the plane parallel to both
)
is perpendicular to the plane parallel to both ![]() and
and ![]() .
.
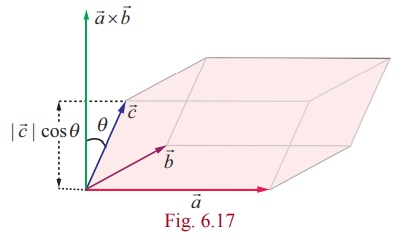
Therefore,
| (![]() Χ
Χ ![]() ) ⋅
) ⋅ ![]() |
is |
|
is | ![]() Χ
Χ ![]() ||
|| ![]() ||
cosθ | , where θ is
the angle between
||
cosθ | , where θ is
the angle between ![]() Χ
Χ ![]() and . From Fig.
6.17, we observe that |
and . From Fig.
6.17, we observe that | ![]() |
| cosθ | is the height
of the parallelepiped formed by using the three
vectors as adjacent vectors. Thus, | (
|
| cosθ | is the height
of the parallelepiped formed by using the three
vectors as adjacent vectors. Thus, | (![]() Χ
Χ ![]() ) ⋅
) ⋅ ![]() |
is the volume of the parallelepiped.
|
is the volume of the parallelepiped.
The
following theorem is useful for computing scalar triple products.
1.
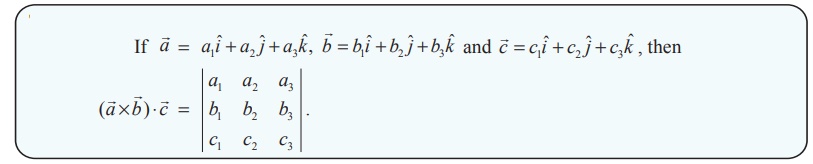
Proof
By
definition, we have
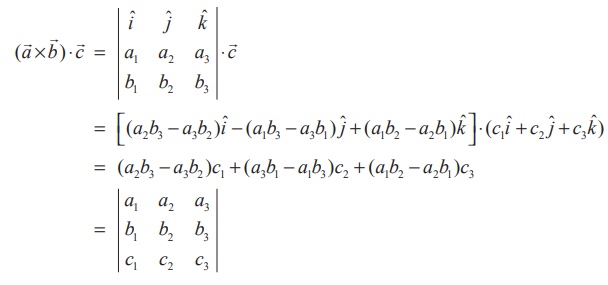
which
completes the proof of the theorem.
Properties
of the scalar triple product
2.
For
any three vectors ![]() ,
, ![]() and
and ![]() ,
(
,
(![]() Χ
Χ ![]() ) ⋅
) ⋅ ![]() =
= ![]() ⋅ (
⋅ (![]() Χ
Χ ![]() )
.
)
.
Proof
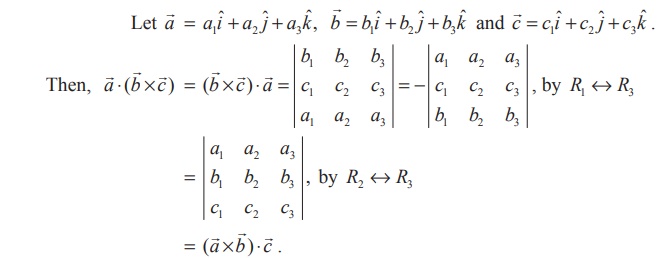
Hence
the theorem is proved.
3.
The
scalar triple product preserves addition and scalar multiplication. That is,
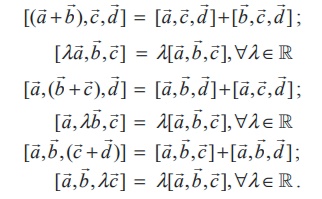
Proof
Using
the properties of scalar product and vector product, we get
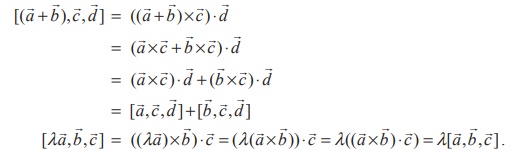
Using
the first statement of this result, we get the following.
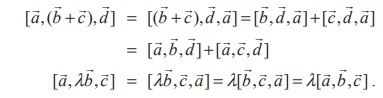
Similarly,
the remaining equalities are proved.
We
have studied about coplanar vectors in XI standard as three nonzero vectors of
which, one can be expressed as a linear combination of the other two. Now we
use scalar triple product for the characterisation of
coplanar vectors.
4.
The
scalar triple product of three non-zero vectors is zero if, and only if, the
three vectors are coplanar.
Proof
Let ![]() ,
, ![]() ,
, ![]() be
any three non-zero vectors. Then,
be
any three non-zero vectors. Then,
![]() Χ
Χ ![]() ⋅
⋅ ![]() =
0 ⇔
=
0 ⇔ ![]() is
perpendicular to
is
perpendicular to ![]() Χ
Χ ![]()
⇔ ![]() lies
in the plane which is parallel to both
lies
in the plane which is parallel to both ![]() and
and ![]()
![]() ,
, ![]() ,
, ![]() are
coplanar.
are
coplanar.
5.
Three
vectors ![]() ,
, ![]() ,
, ![]() are
coplanar if, and only if, there exist scalars r, s, t ∈ R such that atleast one of them is non-zero and r
are
coplanar if, and only if, there exist scalars r, s, t ∈ R such that atleast one of them is non-zero and r![]() + s
+ s![]() + t
+ t![]() =
= ![]() .
.
Proof
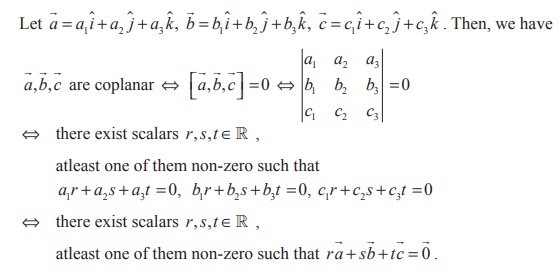
6

Proof
Applying
the distributive law of cross product and using
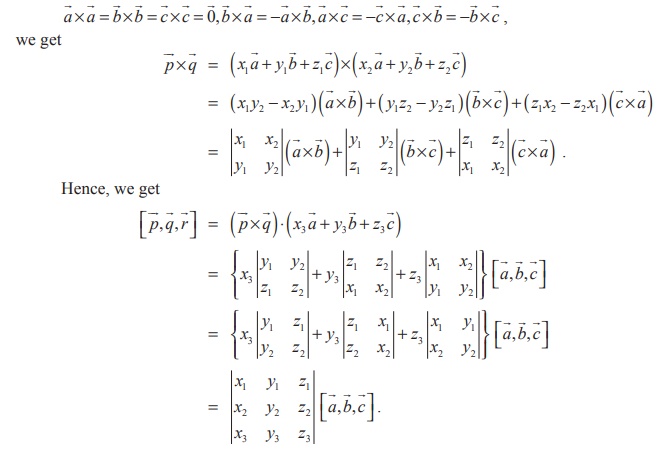
Vector
triple product
5.
For
a given set of three vectors ![]() ,
, ![]() ,
, ![]() ,
the vector
,
the vector ![]() Χ(
Χ(![]() Χ
Χ ![]() )
is called a vector triple product.
)
is called a vector triple product.
Proof:
Given
any three vectors ![]() ,
, ![]() ,
,![]() the
following are vector triple products :
the
following are vector triple products :
![]()
Using
the well known properties of the vector product, we
get the following theorem.
7
The
vector triple product satisfies the following properties.
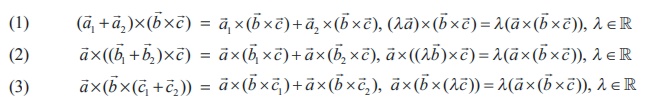
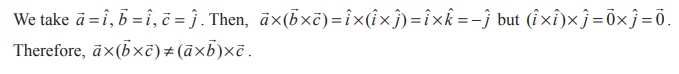
The following theorem gives a simple formula to
evaluate the vector triple product.
8.
(Vector Triple product expansion)
For
any three vectors ![]() ,
, ![]() ,
, ![]() we
have
we
have ![]()
Proof
Let
us choose the coordinate axes as follows :
Let x -axis
be chosen along the line of action of ![]() , y -axis
be chosen in the plane passing through
, y -axis
be chosen in the plane passing through ![]() and
parallel to
and
parallel to ![]() ,
and z -axis be chosen perpendicular to the plane
containing
,
and z -axis be chosen perpendicular to the plane
containing ![]() and
and ![]() .
Then, we have
.
Then, we have
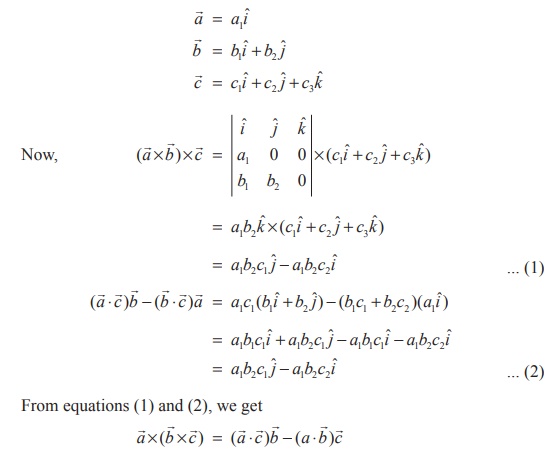
Jacobis Identity and Lagranges Identity
9 . (Jacobis identity)
For any three vectors ![]() ,
, ![]() ,
, ![]() , we have
, we have ![]() =
= ![]() .
.
Proof
Using vector triple product expansion, we have
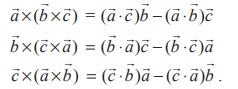
Adding the above equations and using the scalar product of two
vectors is commutative, we get
![]() .
.
10. (Lagranges identity)
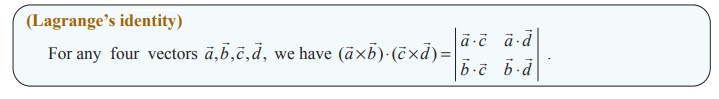
Proof
Since dot and cross can be interchanged in a scalar product, we
get
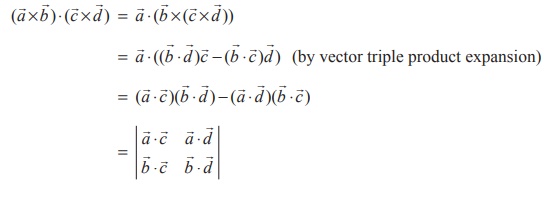
11
Prove that ![]()
Solution
Using the definition of the scalar triple product, we get
![]() ..............(1)
..............(1)
By treating (![]() Χ
Χ ![]() ) as the first vector in the vector triple product, we find
) as the first vector in the vector triple product, we find
![]()
Using this value in (1), we get
![]()
12 .Prove that ![]() .
.
Solution
Treating (![]() Χ
Χ ![]() ) as the first vector on
the right hand side of the given equation and using the vector triple product
expansion, we get
) as the first vector on
the right hand side of the given equation and using the vector triple product
expansion, we get
![]()
13. For any four vectors ![]() ,
, ![]() ,
, ![]() ,
, ![]() , we have
, we have
![]()
Solution
Taking ![]() = (
= (![]() Χ
Χ ![]() )
as a single vector and using the vector triple product expansion,
we get
)
as a single vector and using the vector triple product expansion,
we get
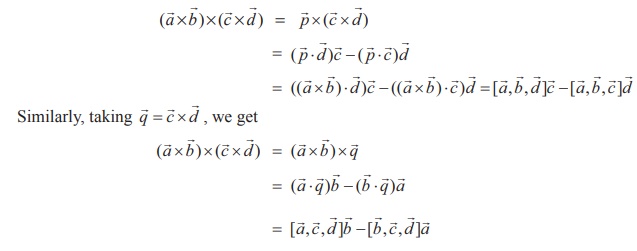
14.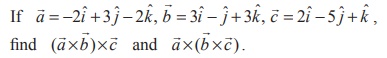
State whether they are equal.
Solution
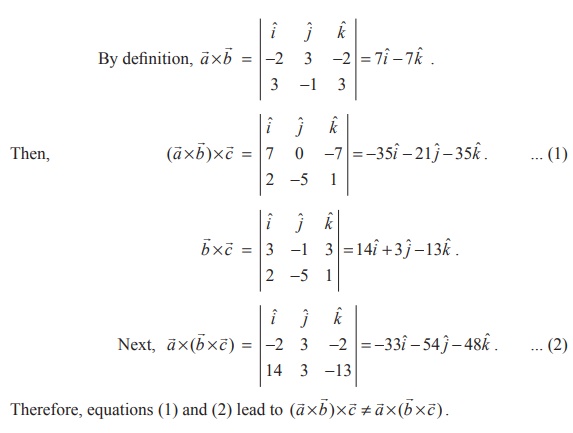
15. 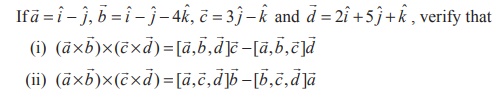
Solution (i)
By definition,
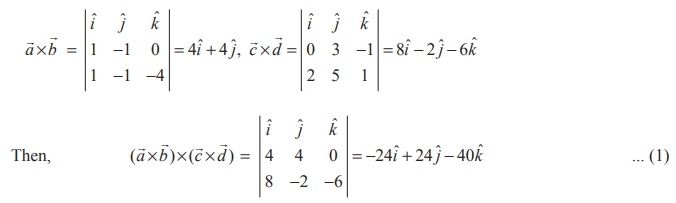
On the other hand, we have
![]()
Therefore, from equations (1) and (2), identity (i) is verified.
The verification of identity (ii) is left as an exercise to the
reader.
Application
of Vectors to 3-Dimensional Geometry :
Vectors provide an elegant approach to study straight
lines and planes in three dimension. All straight lines and planes are subsets
of R3. For brevity, we shall call a straight line simply
as line. A plane is a surface which is understood as a set P of
points in R3 such that , if A, B,
and C are any three non-collinear points of P ,
then the line passing through any two of them is a subset of P. Two
planes are said to be intersecting if they have at least one point in common
and at least one point which lies on one plane but not on the other. Two planes
are said to be coincident if they have exactly the same points. Two planes are
said to be parallel but not coincident if they have no point in common.
1.
Different forms of equation of a straight line
A
straight line can be uniquely fixed if
![]() a
point on the straight line and the direction of the straight line are given
a
point on the straight line and the direction of the straight line are given
![]() two
points on the straight line are given
two
points on the straight line are given
We find equations of a straight line in vector and
Cartesian form. To find the equation of a straight line in vector form, an
arbitrary point P with position vector ![]() on
the straight line is taken and a relation satisfied by
on
the straight line is taken and a relation satisfied by ![]() is
obtained by using the given conditions. This relation is called the vector
equation of the straight line. A vector equation of a straight line may or may
not involve parameters. If a vector equation involves parameters, then it is
called a vector equation in parametric form.
If no parameter is involved, then the equation is called a vector
equation in non parametric form.
is
obtained by using the given conditions. This relation is called the vector
equation of the straight line. A vector equation of a straight line may or may
not involve parameters. If a vector equation involves parameters, then it is
called a vector equation in parametric form.
If no parameter is involved, then the equation is called a vector
equation in non parametric form.
2.
A point on the straight line and the
direction of the straight line are given
(A)
Parametric form of vector equation
1.
The vector equation of a straight line passing
through a fixed point with position vector ![]() and
parallel to a given vector
and
parallel to a given vector ![]() is
is ![]() =
= ![]() + t
+ t![]() ,
where t ∈ R.
,
where t ∈ R.
Proof
If ![]() is
the position vector of a given point A and
is
the position vector of a given point A and ![]() is
the position vector of an arbitrary point
P on the straight line, then
is
the position vector of an arbitrary point
P on the straight line, then
![]() =
= ![]() -
- ![]() .
.
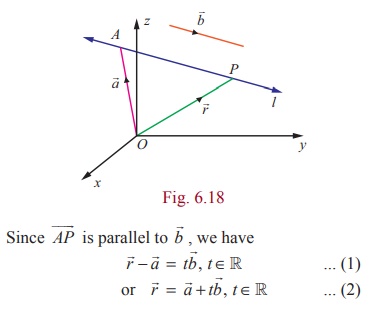
This
is the vector equation of the straight line in parametric form.
(b) Non-parametric form of vector equation
Since ![]() is
parallel to
is
parallel to ![]() ,
we have
,
we have ![]() Χ
Χ ![]() =
= ![]()
That
is, (![]() −
− ![]() )
Χ
)
Χ ![]() =
0 .
=
0 .
This
is known as the vector equation of
the straight line in non-parametric form.
(c)
Cartesian equation
Suppose P is
(x, y, z) , A is
(x1 , y1 , z1 )
and ![]() = b1 i + b2 j + b3 k .
Then, substituting
= b1 i + b2 j + b3 k .
Then, substituting ![]() = x i + y j + z k ,
= x i + y j + z k , ![]() = x1i + y1 j + z1 k in
(1) and comparing the coefficients of i ,
j, k , we get
= x1i + y1 j + z1 k in
(1) and comparing the coefficients of i ,
j, k , we get
x − x1 = tb1 , y − y1 = tb2 , z − z1 = tb3
.(4)
Conventionally
(4) can be written as
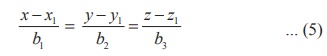
which
are called the Cartesian equations or
symmetric equations of a straight line passing
through the point (x1, y1 , z1)
and parallel to a vector with direction ratios b1, b2, b3.
3.
Straight Line passing through two given points
(a) Parametric
form of vector equation
Theorem
6.12
The
parametric form of vector equation of a line passing through two given points
whose position vectors are ![]() and
and ![]() respectively
is
respectively
is ![]() , t ∈ R.
, t ∈ R.
(b)
Non-parametric form of vector equation
The
above equation can be written equivalently in non-parametric form of vector
equation as
![]() =
= ![]()
(c)
Cartesian form of equation
Suppose P is
(x, y, z) , A is
(x1, y1 , z1 )
and B is (x2 , y2 , z2).
Then substituting ![]() = x i + y j + z k ,
= x i + y j + z k , ![]() = x1i + y1 j + z1k
and
= x1i + y1 j + z1k
and ![]() = x2i + y2 j + z2k in
theorem 6.12 and comparing the coefficients of i , j, k ,
we get x − x1 = t(x2 − x1), y − y1 = t( y2 − y1), z − z1 = t(z2 − z1 )
and so the Cartesian equations of a line passing through two given points
(x1, y1, z1)
and (x2, y2, z2) are
given by
= x2i + y2 j + z2k in
theorem 6.12 and comparing the coefficients of i , j, k ,
we get x − x1 = t(x2 − x1), y − y1 = t( y2 − y1), z − z1 = t(z2 − z1 )
and so the Cartesian equations of a line passing through two given points
(x1, y1, z1)
and (x2, y2, z2) are
given by
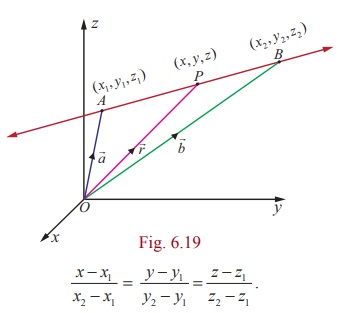
From
the above equation, we observe that the direction ratios of a line passing
through two given points (x1 , y1 , z1)
and (x2 , y2 , z2 )
are given by x2 − x1 , y2 − y1 , z2 − z1,
which are also given by any three numbers proportional to them and in
particular x1 − x2 , y1 − y2 , z1 − z2.
2. A
straight line passes through the point (1, 2, −3) and parallel to 4i
+ 5 j − 7k . Find (i) vector equation in parametric form (ii) vector equation
in non-parametric form (iii) Cartesian equations of the straight line.
Solution
The
required line passes through (1, 2, −3) . So,
the position vector of the point is i +
2 j − 3k.
Let ![]() = i +
2 j −
3k and
= i +
2 j −
3k and ![]() =
4i +
5 j −
7k .
Then, we have
=
4i +
5 j −
7k .
Then, we have
Let
a = i + 2 j - 3k and b = 4i + 5 j - 7k . Then, we have
(i) vector equation of the required
straight line in parametric form is ![]() =
= ![]() +
t
+
t![]() ,
t ∈ R.
,
t ∈ R.
Therefore, ![]() =
(i + 2 j - 3 k ) + t(4 i
+ 5 j - 7 k ), t∈ R..
=
(i + 2 j - 3 k ) + t(4 i
+ 5 j - 7 k ), t∈ R..
(ii)
vector equation of the required straight line in
non-parametric form is ( ![]() -
- ![]() )
Χ
)
Χ ![]() =
= ![]() .
.
Therefore,
( ![]() -
(i + 2 j - 3 k )) Χ (4
i + 5 j - 7 k )
=
-
(i + 2 j - 3 k )) Χ (4
i + 5 j - 7 k )
= ![]() .
.
(iii)
Cartesian equations of the required line are (x - x1) / b1 =
y - y1 / b1 = (z - z1) / b1.
Here,
(x1 , y1 , z1)
= (1, 2, -3) and direction ratios of the required line are proportional to 4,
5, -7 . Therefore, Cartesian equations of the straight line are (x -1)/4
= (y 2)/5 = (z + 3)/-7.
3. The
vector equation in parametric form of a line is ![]() =
(3 i − 2 j + 6
k ) + t(2 i −
j + 3 k ) . Find (i) the
direction cosines of the straight line (ii) vector equation in non-parametric
form of the line (iii)Cartesian equations of the line.
=
(3 i − 2 j + 6
k ) + t(2 i −
j + 3 k ) . Find (i) the
direction cosines of the straight line (ii) vector equation in non-parametric
form of the line (iii)Cartesian equations of the line.
Solution
Comparing
the given equation with equation of a straight line ![]() =
= ![]() + t
+ t![]() ,
we have
,
we have ![]() =
3 i − 2 j + 6
k and
=
3 i − 2 j + 6
k and ![]() =
2i − j + 3k .
Therefore,
=
2i − j + 3k .
Therefore,
(i) If ![]() =
b1i + b2j + b3k
, then direction ratios of the straight line are
b1 , b2 , b3. Therefore, direction ratios
of the given straight line are proportional to 2, -1, 3 ,
and hence the direction cosines of the given straight line are
=
b1i + b2j + b3k
, then direction ratios of the straight line are
b1 , b2 , b3. Therefore, direction ratios
of the given straight line are proportional to 2, -1, 3 ,
and hence the direction cosines of the given straight line are 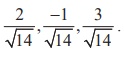 .
.
(ii)
vector equation of the straight line in non-parametric
form is given by ( ![]() -
- ![]() )
Χ
)
Χ ![]() =
= ![]() .
Therefore, (
.
Therefore, ( ![]() -
(3 i - 2 j + 6 k ))
x(2 i - j + 3 k )
= 0 .
-
(3 i - 2 j + 6 k ))
x(2 i - j + 3 k )
= 0 .
(iii)
Here (x1 , y1 , z1 )
= (3, -2, 6) and the direction ratios are proportional to 2, -1, 3 .
Therefore,
Cartesian equations of the straight line are (x 3)/2 = (y + 2)/-1 = (z 6)/3
4. Find
the vector equation in parametric form and Cartesian equations of the line
passing through (−4, 2, −3) and is parallel to the line 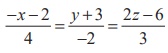
Solution
Rewriting
the given equations as 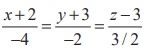 and
comparing with
and
comparing with 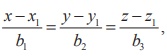
We
have 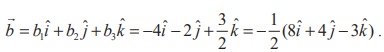
Clearly, ![]() is
parallel to the vector 8i + 4j - 3k . Therefore, a vector equation of the required straight
line passing through the given point (-4, 2, -3) and parallel to the vector 8i
+ 4j - 3k in parametric form is
is
parallel to the vector 8i + 4j - 3k . Therefore, a vector equation of the required straight
line passing through the given point (-4, 2, -3) and parallel to the vector 8i
+ 4j - 3k in parametric form is
![]() =
(-4i + 2j - 3k) + t(8i
+ 4j - 3k), t ∈ R.
=
(-4i + 2j - 3k) + t(8i
+ 4j - 3k), t ∈ R.
Therefore,
Cartesian equations of the required straight line are given by
(x
+ 4) / 8 = (y 2) / 4 = (z + 3) / -3 .
5. Find
the vector equation in parametric form and Cartesian equations of a straight
passing through the points (−5, 7, −4) and (13, −5, 2) . Find the point where the straight line crosses the xy -plane.
Solution
The
straight line passes through the points (−5, 7, −4) and (13,
−5, 2) , and therefore, direction ratios of the
straight line joining these two points are 18, −12, 6 . That is 3,
−2,1.
So,
the straight line is parallel to 3i − 2 j + k . Therefore,
Required
vector equation of the straight line in parametric form is ![]() =
(−5i +
7 j −
4k )
+ t(3i −
2j + k )
or
=
(−5i +
7 j −
4k )
+ t(3i −
2j + k )
or ![]() =
(13i − 5j +
2k ) + s(3i −
2j + k )
where s, t ∈ R.
=
(13i − 5j +
2k ) + s(3i −
2j + k )
where s, t ∈ R.
Required
cartesian equations of the
straight line are 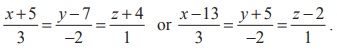
An
arbitrary point on the straight line is of the form
Since
the straight line crosses the xy -plane, the z
-coordinate of the point of intersection is zero. Therefore, we have
t − = 4 0 , that is, t = 4, and hence the
straight line crosses the xy -plane
at (7,−1,0).
6. Find
the angles between the straight line 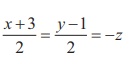 with
coordinate axes.
with
coordinate axes.
Solution
If b
is a unit vector parallel to the given line, then b = 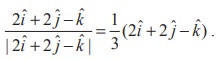 Therefore,
from the definition of direction cosines of b ,
we have
Therefore,
from the definition of direction cosines of b ,
we have
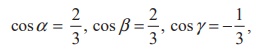
where α , β ,γ are the angles
made by b with the positive x -axis, positive y -axis, and
positive z -axis, respectively. As the angle between the given straight line
with the coordinate axes are same as the angles made by b with the
coordinate axes, we have α = cos-1 (2/3), β = cos-1( 2/3), γ = cos-1(-1/3), respectively.
4.
Angle between two straight lines
(a) Vector
form
The
acute angle between two given straight lines
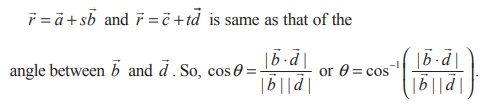
(b)
Cartesian form
If
two lines are given in Cartesian form as ![]() then
the acute angle θ between the two given lines is given by
then
the acute angle θ between the two given lines is given by
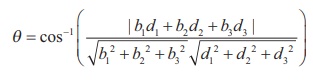
1. Find
the acute angle between the lines ![]() =
(i + 2j + 4k ) + t(2i + 2j + k ) and
the straight line passing through the points (5,1, 4) and (9, 2,12) .
=
(i + 2j + 4k ) + t(2i + 2j + k ) and
the straight line passing through the points (5,1, 4) and (9, 2,12) .
Solution
We
know that the line ![]() =
(i +
2j + 4k )
+ t(2i +
2j + k )
is parallel to the vector 2i +
2j + k.
=
(i +
2j + 4k )
+ t(2i +
2j + k )
is parallel to the vector 2i +
2j + k.
Direction
ratios of the straight line joining the two given points (5,1,
4) and (9, 2,12) are 4,1,8 and hence this line is parallel
to the vector 4i + j + 8k .
Therefore,
the acute angle between the given two straight lines is
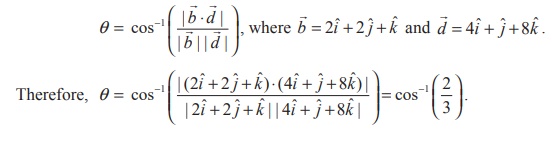
2. Find
the acute angle between the straight lines 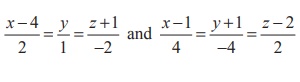 and
state whether they are parallel or perpendicular.
and
state whether they are parallel or perpendicular.
Solution
Comparing
the given lines with the general Cartesian equations of straight lines,
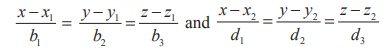
we
find (b1 , b2 , b3 )
= (2,1, −2) and (d1 , d2 , d3 )
= (4, −4, 2) . Therefore, the acute angle between the two straight lines
is
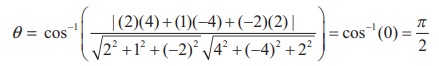
Thus
the two straight lines are perpendicular.
3. Show
that the straight line passing through the points A(6,
7, 5) and B(8,10, 6) is perpendicular to the straight line passing
through the points C(10, 2, −5) and D(8, 3,
−4) .
Solution
The
straight line passing through the points A(6, 7, 5) and B(8,10,
6) is parallel to the vector ![]() =
= ![]() =
= ![]() −
− ![]() =
2i + 3 j + k and the straight line passing
through the points C(10, 2, −5) and D(8, 3,
−4) is parallel to the vector
=
2i + 3 j + k and the straight line passing
through the points C(10, 2, −5) and D(8, 3,
−4) is parallel to the vector ![]() =
= ![]() =
−2i + j + k . Therefore, the angle
between the two straight lines is the angle between the two vectors
=
−2i + j + k . Therefore, the angle
between the two straight lines is the angle between the two vectors ![]() and
and ![]() .
Since
.
Since
![]()
the two vectors are perpendicular,
and hence the two straight lines are perpendicular.
A
point on the straight line and the direction of the straight line
are given
(A)
Parametric form of vector equation
1. The vector equation of a
straight line passing through a fixed point with position vector ![]() and
parallel to a given vector
and
parallel to a given vector ![]() is
is ![]() =
= ![]() + t
+ t![]() ,
where t∈ R.
,
where t∈ R.
Proof
If ![]() is
the position vector of a given point A and
is
the position vector of a given point A and ![]() is
the position vector of an arbitrary point
P on the straight line, then
is
the position vector of an arbitrary point
P on the straight line, then
![]() =
= ![]() -
- ![]() .
.

This
is the vector equation of the straight line in parametric form.
(b) Non-parametric form of vector equation
Since ![]() is
parallel to
is
parallel to ![]() ,
we have
,
we have ![]() Χ
Χ ![]() =
= ![]()
That
is, (![]() −
− ![]() )
Χ
)
Χ ![]() =
0 .
=
0 .
This
is known as the vector equation of
the straight line in non-parametric form.
(c)
Cartesian equation
Suppose P is
(x, y, z) , A is
(x1 , y1 , z1 ) and ![]() = b1 i + b2 j + b3 k .
Then, substituting
= b1 i + b2 j + b3 k .
Then, substituting ![]() = x i + y j + z k ,
= x i + y j + z k , ![]() = x1i + y1 j + z1 k in
(1) and comparing the coefficients of i ,
j, k , we get
= x1i + y1 j + z1 k in
(1) and comparing the coefficients of i ,
j, k , we get
x − x1 = tb1 , y − y1 = tb2 , z − z1 = tb3
.(4)
Conventionally
(4) can be written as
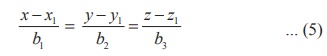
which
are called the Cartesian equations or
symmetric equations of a straight line passing
through the point (x1, y1 , z1) and
parallel to a vector with direction ratios b1, b2, b3.
Straight Line passing through
two given points
(a) Parametric form of
vector equation
The
parametric form of vector equation of a line passing through two given points
whose position vectors are ![]() and
and ![]() respectively
is
respectively
is ![]() , t ∈ R.
, t ∈ R.
(b)
Non-parametric form of vector equation
The
above equation can be written equivalently in non-parametric form of vector
equation as
![]() =
= ![]()
(c) Cartesian form of equation
Suppose P is
(x, y, z) , A is
(x1, y1 , z1 ) and B is
(x2 , y2 , z2). Then
substituting ![]() = x i + y
j + z k ,
= x i + y
j + z k , ![]() = x1i + y1 j + z1k
and
= x1i + y1 j + z1k
and ![]() = x2i + y2 j +z2k in
theorem 6.12 and comparing the coefficients of i , j, k ,
we get x − x1 = t(x2 − x1), y − y1 = t( y2 − y1), z − z1 = t(z2 − z1 )
and so the Cartesian equations of a line passing through two given points
(x1, y1, z1) and (x2, y2, z2) are
given by
= x2i + y2 j +z2k in
theorem 6.12 and comparing the coefficients of i , j, k ,
we get x − x1 = t(x2 − x1), y − y1 = t( y2 − y1), z − z1 = t(z2 − z1 )
and so the Cartesian equations of a line passing through two given points
(x1, y1, z1) and (x2, y2, z2) are
given by

From
the above equation, we observe that the direction ratios of a line passing
through two given points (x1 , y1 , z1)
and (x2 , y2 , z2 ) are given by x2− x1 , y2 − y1 , z2 − z1,
which are also given by any three numbers proportional to them and in
particular x1 − x2 , y1 − y2 , z1 − z2.
1.
A straight line passes through
the point (1, 2, −3) and parallel to 4i + 5 j −
7k . Find (i) vector
equation in parametric form (ii) vector equation in non-parametric form (iii)
Cartesian equations of the straight line.
Solution
The
required line passes through (1, 2, −3) . So,
the position vector of the point is i +
2 j − 3k.
Let ![]() = i +
2 j −
3k and
= i +
2 j −
3k and ![]() =
4i +
5 j −
7k .
Then, we have
=
4i +
5 j −
7k .
Then, we have
Let
a = i + 2 j - 3k and b = 4i + 5 j - 7k . Then, we have
(i) vector equation of the required
straight line in parametric form is ![]() =
= ![]() +
t
+
t![]() ,
t ∈ R.
,
t ∈ R.
Therefore, ![]() =
(i + 2 j - 3 k ) + t(4 i
+ 5 j - 7 k ), t∈ R..
=
(i + 2 j - 3 k ) + t(4 i
+ 5 j - 7 k ), t∈ R..
(ii)
vector equation of the required straight line in
non-parametric form is ( ![]() -
- ![]() )
Χ
)
Χ ![]() =
= ![]() .
.
Therefore,
( ![]() -
(i + 2 j - 3 k )) Χ (4
i + 5 j - 7 k )
=
-
(i + 2 j - 3 k )) Χ (4
i + 5 j - 7 k )
= ![]() .
.
(iii)
Cartesian equations of the required line are (x - x1) / b1 = y -
y1 / b1 = (z - z1) / b1.
Here,
(x1 , y1 , z1)
= (1, 2, -3) and direction ratios of the required line are proportional to 4,
5, -7 . Therefore, Cartesian equations of the straight line are (x -1)/4
= (y 2)/5 = (z + 3)/-7.
2.
The vector equation in
parametric form of a line is ![]() =
(3 i − 2 j + 6
k ) + t(2 i −
j + 3 k ) . Find (i) the
direction cosines of the straight line (ii) vector equation in non-parametric
form of the line (iii)Cartesian equations of the line.
=
(3 i − 2 j + 6
k ) + t(2 i −
j + 3 k ) . Find (i) the
direction cosines of the straight line (ii) vector equation in non-parametric
form of the line (iii)Cartesian equations of the line.
Solution
Comparing
the given equation with equation of a straight line ![]() =
= ![]() + t
+ t![]() ,
we have
,
we have ![]() =
3 i − 2 j + 6
k and
=
3 i − 2 j + 6
k and ![]() =
2i − j + 3k .
Therefore,
=
2i − j + 3k .
Therefore,
(i) If ![]() = b1i
+ b2j + b3k
, then direction ratios of the straight line are
b1 , b2 , b3. Therefore, direction ratios of the given straight line
are proportional to 2, -1, 3 , and hence the direction
cosines of the given straight line are
= b1i
+ b2j + b3k
, then direction ratios of the straight line are
b1 , b2 , b3. Therefore, direction ratios of the given straight line
are proportional to 2, -1, 3 , and hence the direction
cosines of the given straight line are 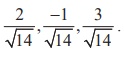 .
.
(ii) vector equation of the straight line in non-parametric form
is given by ( ![]() -
- ![]() ) Χ
) Χ ![]() =
= ![]() .
Therefore, (
.
Therefore, ( ![]() -
(3 i - 2 j + 6 k ))
x(2 i - j + 3 k) =
0 .
-
(3 i - 2 j + 6 k ))
x(2 i - j + 3 k) =
0 .
(iii) Here (x1 , y1 , z1 ) = (3, -2, 6) and the direction
ratios are proportional to 2, -1, 3 .
Therefore,
Cartesian equations of the straight line are (x 3)/2 = (y + 2)/-1 = (z 6)/3
3.
Find the vector equation in
parametric form and Cartesian equations of the line passing through (−4,
2, −3) and is parallel to the line 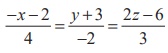
Solution
Rewriting
the given equations as 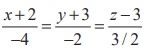 and
comparing with
and
comparing with 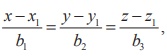
We
have 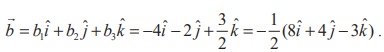
Clearly, ![]() is
parallel to the vector 8i + 4j - 3k . Therefore, a vector equation of the required straight
line passing through the given point (-4, 2, -3) and parallel to the vector 8i
+ 4j - 3k in parametric form is
is
parallel to the vector 8i + 4j - 3k . Therefore, a vector equation of the required straight
line passing through the given point (-4, 2, -3) and parallel to the vector 8i
+ 4j - 3k in parametric form is
![]() =
(-4i + 2j - 3k) + t(8i
+ 4j - 3k), t ∈ R.
=
(-4i + 2j - 3k) + t(8i
+ 4j - 3k), t ∈ R.
Therefore,
Cartesian equations of the required straight line are given by
(x
+ 4) / 8 = (y 2) / 4 = (z + 3) / -3 .
4.
Find the vector equation in parametric
form and Cartesian equations of a straight passing through the points
(−5, 7, −4) and (13, −5, 2) . Find
the point where the straight line crosses the xy -plane.
Solution
The
straight line passes through the points (−5, 7, −4) and (13,
−5, 2) , and therefore, direction ratios of the
straight line joining these two points are 18, −12, 6 . That is 3,
−2,1.
So,
the straight line is parallel to 3i − 2 j + k . Therefore,
Required
vector equation of the straight line in parametric form is ![]() =
(−5i +
7 j −
4k )
+ t(3i −
2j + k )
or
=
(−5i +
7 j −
4k )
+ t(3i −
2j + k )
or ![]() =
(13i − 5j +
2k ) + s(3i −
2j +k )
where s, t ∈ R.
=
(13i − 5j +
2k ) + s(3i −
2j +k )
where s, t ∈ R.
Required
cartesian equations of the
straight line are 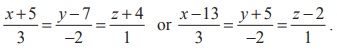
An
arbitrary point on the straight line is of the form
Since
the straight line crosses the xy -plane, the z
-coordinate of the point of intersection is zero. Therefore, we have
t − = 4 0 , that is, t = 4, and hence the
straight line crosses the xy -plane
at (7,−1,0).
5.
Find the angles between the
straight line 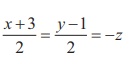 with
coordinate axes.
with
coordinate axes.
Solution
If b
is a unit vector parallel to the given line, then b = 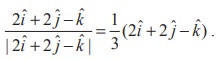 Therefore,
from the definition of direction cosines of b ,
we have
Therefore,
from the definition of direction cosines of b ,
we have
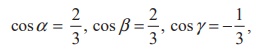
where α , β ,γ are the
angles made by b with the positive x -axis, positive y -axis, and
positive z -axis, respectively. As the angle between the given straight line
with the coordinate axes are same as the angles made by b with the
coordinate axes, we have α = cos-1 (2/3), β = cos-1( 2/3), γ = cos-1(-1/3), respectively.
Angle
between two straight lines
(a) Vector
form
The
acute angle between two given straight lines
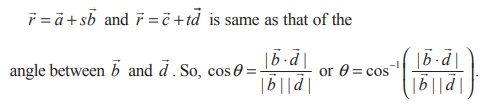
(b)
Cartesian form
If
two lines are given in Cartesian form as ![]() then
the acute angle θ between the two given lines is given by
then
the acute angle θ between the two given lines is given by
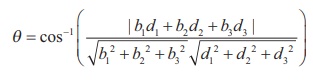
1.
Find
the acute angle between the lines ![]() =
(i + 2j + 4k ) + t(2i + 2j + k ) and
the straight line passing through the points (5,1, 4) and (9, 2,12) .
=
(i + 2j + 4k ) + t(2i + 2j + k ) and
the straight line passing through the points (5,1, 4) and (9, 2,12) .
Solution
We
know that the line ![]() =
(i +
2j + 4k )
+ t(2i +
2j + k )
is parallel to the vector 2i +
2j + k.
=
(i +
2j + 4k )
+ t(2i +
2j + k )
is parallel to the vector 2i +
2j + k.
Direction
ratios of the straight line joining the two given points (5,1,
4) and (9, 2,12) are 4,1,8 and hence this line is parallel
to the vector 4i + j + 8k .
Therefore,
the acute angle between the given two straight lines is
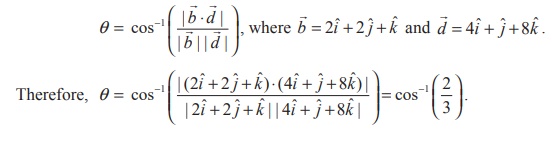
2. Find
the acute angle between the straight lines 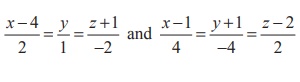 and
state whether they are parallel or perpendicular.
and
state whether they are parallel or perpendicular.
Solution
Comparing
the given lines with the general Cartesian equations of straight lines,
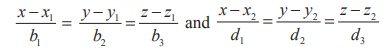
we
find (b1 , b2 , b3 ) = (2,1,
−2) and (d1 , d2 , d3 ) =
(4, −4, 2) . Therefore, the acute angle between the two straight lines is
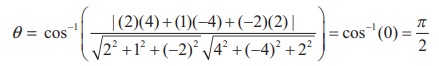
Thus
the two straight lines are perpendicular.
3. Show
that the straight line passing through the points A(6,
7, 5) and B(8,10, 6) is perpendicular to the straight line passing
through the points C(10, 2, −5) and D(8, 3,
−4) .
Solution
The
straight line passing through the points A(6, 7, 5) and B(8,10,
6) is parallel to the vector ![]() =
= ![]() =
= ![]() −
− ![]() =
2i + 3 j + k and the straight line passing
through the points C(10, 2, −5) and D(8, 3,
−4) is parallel to the vector
=
2i + 3 j + k and the straight line passing
through the points C(10, 2, −5) and D(8, 3,
−4) is parallel to the vector ![]() =
= ![]() =
−2i + j + k . Therefore, the angle
between the two straight lines is the angle between the two vectors
=
−2i + j + k . Therefore, the angle
between the two straight lines is the angle between the two vectors ![]() and
and ![]() .
Since
.
Since
![]()
the two vectors are perpendicular,
and hence the two straight lines are perpendicular.
4. Show
that the lines ![]() and
and 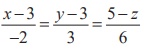 are parallel
are parallel
Solution
We
observe that the straight line ![]() is
parallel to the vector 4i - 6 j +12k and the
straight line
is
parallel to the vector 4i - 6 j +12k and the
straight line 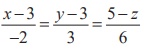 is
parallel to the vector -2i + 3j - 6k.
is
parallel to the vector -2i + 3j - 6k.
Since
4i - 6j +12k = -2(-2i + 3j -
6k) , the two vectors are parallel, and hence
the two straight lines are parallel.
Point
of intersection of two straight lines
If 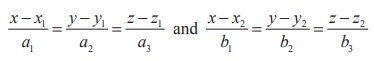 are
two lines, then every point on the line is of the form (x1 + sa1 , y1 + sa2 , z1 + sa3 )
and (x2 + tb1 , y2 + tb2 , z2 + tb3 )
respectively. If the lines are intersecting, then there
must be a common point. So, at the point of intersection, for some values
of s and t , we have
are
two lines, then every point on the line is of the form (x1 + sa1 , y1 + sa2 , z1 + sa3 )
and (x2 + tb1 , y2 + tb2 , z2 + tb3 )
respectively. If the lines are intersecting, then there
must be a common point. So, at the point of intersection, for some values
of s and t , we have
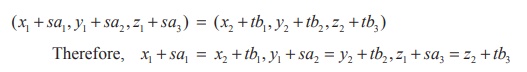
By
solving any two of the above three equations, we obtain the values of s and t . If s and t satisfy the remaining equation, the
lines are intersecting lines. Otherwise the lines are non-intersecting
. Substituting the value of s ,
(or by substituting the value of t ), we get the point of
intersection of two lines.
If
the equations of straight lines are given in vector form, write them in cartesian form and proceed
as above to find the point of intersection.
1. Find
the point of intersection of the lines 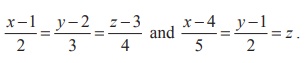
Solution
Every
point on the line 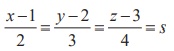 (say)
is of the form (2s +1, 3s + 2, 4s + 3) and every point on the line
(say)
is of the form (2s +1, 3s + 2, 4s + 3) and every point on the line 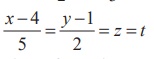 (say)
is of the form (5t + 4, 2t +1, t) . So, at
the point of intersection, for some values of s and t ,
we have
(say)
is of the form (5t + 4, 2t +1, t) . So, at
the point of intersection, for some values of s and t ,
we have
(2s +1,
3s + 2, 4s + 3) = (5t + 4, 2t +1, t)
Therefore,
2s − 5t = 3, 3s − 2t =
−1 and 4s − t = −3 . Solving the first two equations we get t =
−1, s = −1 . These values
of s and t satisfy
the third equation. Therefore, the given lines intersect. Substituting, these
values of t or s in the respective points,
the point of intersection is (−1, −1, −1) .
Shortest distance between two straight lines
We have just explained how the point of intersection of two lines
are found and we have also studied how to determine whether the given two lines
are parallel or not.
1.
Find the parametric form
of vector equation of a straight line passing through the point of intersection
of the straight lines ![]() and perpendicular to both straight lines.
and perpendicular to both straight lines.
Solution
The Cartesian equations of the straight line ![]() = (i
+ 3 j − k )
+ t(2i + 3 j + 2k ) is
= (i
+ 3 j − k )
+ t(2i + 3 j + 2k ) is
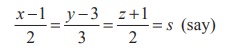
Then any point on this line is of the form (2s +1, 3s +
3, 2s -1) ... (1)
The Cartesian equation of the second line is (x 2)/1
= (y 4)/2 = (z + 3)/4 = t (say)
Then any point on this line is of the form (t + 2, 2t + 4, 4t - 3)
If the given lines intersect, then there must be a common point.
Therefore, for some s, t ∈ R, we have (2s +1, 3s + 3, 2s −1)
= (t + 2, 2t + 4, 4t − 3) .
Equating the coordinates of x, y and z we
get
2s − t = 1, 3s −
2t = 1 and s − 2t = −1.
Solving the first two of the above three equations, we get s =
1 and t = 1. These values of s and t satisfy the third equation. So, the lines are intersecting.
Now, using the value of s in
(1) or the value of t in (2), the point of intersection (3, 6,1) of these two straight lines is obtained.
If we take ![]() = 2i + 3j + 2k
and
= 2i + 3j + 2k
and ![]() = i + 2j +
4k then
= i + 2j +
4k then 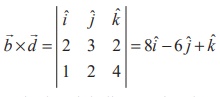 is a vector perpendicular to both
the given straight lines. Therefore, the required straight line passing through
(3, 6,1) and perpendicular to both the given straight
lines is the same as the straight line passing through (3, 6,1) and parallel to
8i − 6 j + k . Thus, the equation of
the required straight line is
is a vector perpendicular to both
the given straight lines. Therefore, the required straight line passing through
(3, 6,1) and perpendicular to both the given straight
lines is the same as the straight line passing through (3, 6,1) and parallel to
8i − 6 j + k . Thus, the equation of
the required straight line is
![]()
2.
Determine whether the pair of straight
lines ![]() = (2i + 6j +
3k ) + t(2i + 3j +
4k ) ,
= (2i + 6j +
3k ) + t(2i + 3j +
4k ) , ![]() = (2j −
3k ) + s(i +
2j + 3k ) are parallel. Find the shortest distance
between them.
= (2j −
3k ) + s(i +
2j + 3k ) are parallel. Find the shortest distance
between them.
Solution
Comparing the given two equations with
![]() =
= ![]() + s
+ s![]() and
and ![]() =
= ![]() + t
+ t![]()
we have ![]() = 2i + 6j + 3k,
= 2i + 6j + 3k, ![]() = 2i + 3j + 4k,
= 2i + 3j + 4k, ![]() = 2j − 3k,
= 2j − 3k, ![]() = i + 2j + 3k
= i + 2j + 3k
Clearly, ![]() is not a scalar multiple of
is not a scalar multiple of ![]() .
So, the two vectors are not parallel and hence the two lines are not parallel.
.
So, the two vectors are not parallel and hence the two lines are not parallel.
The shortest distance between the two straight lines is given by
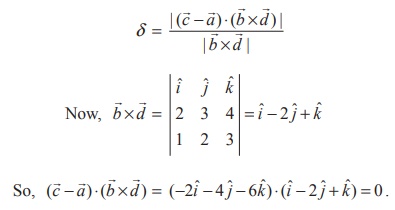
Therefore, the distance between the two given straight lines is zero.Thus, the given lines intersect each other.
3.
Find the shortest
distance between the two given straight lines ![]() = (2i + 3j +
4k ) + t(−2i + j −
2k ) and
= (2i + 3j +
4k ) + t(−2i + j −
2k ) and 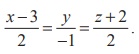
Solution
The parametric form of vector equations of the given straight
lines are
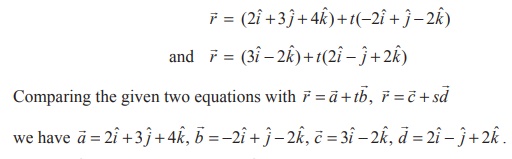
Clearly, ![]() is a scalar multiple of
is a scalar multiple of ![]() ,
and hence the two straight lines are parallel. We know that the shortest
distance between two parallel straight lines is given by d =
,
and hence the two straight lines are parallel. We know that the shortest
distance between two parallel straight lines is given by d =
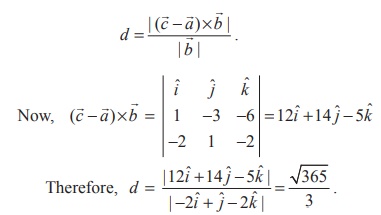
4.
Find the coordinates of
the foot of the perpendicular drawn from the point (−1, 2, 3) to
the straight line ![]() = (i −
4j + 3k ) + t(2i +
3j + k ) . Also, find the shortest distance from
the given point to the straight line.
= (i −
4j + 3k ) + t(2i +
3j + k ) . Also, find the shortest distance from
the given point to the straight line.
Solution
Comparing the given equation ![]() = (i - 4j +
3k ) + t(2i + 3j + k )
with
= (i - 4j +
3k ) + t(2i + 3j + k )
with ![]() =
= ![]() + t
+ t![]() , we get a = i - 4j +
3k , and
, we get a = i - 4j +
3k , and ![]() = 2i + 3j + k . We
denote the given point (-1, 2, 3) by D , and the point
(1, -4, 3) on the straight line by A . If F is the foot of the perpendicular
from D to the straight line, then F is of the form (2t +1, 3t - 4, t + 3)
and
= 2i + 3j + k . We
denote the given point (-1, 2, 3) by D , and the point
(1, -4, 3) on the straight line by A . If F is the foot of the perpendicular
from D to the straight line, then F is of the form (2t +1, 3t - 4, t + 3)
and ![]() = (2t + 2)i
+ (3t - 6) j + tk.
= (2t + 2)i
+ (3t - 6) j + tk.
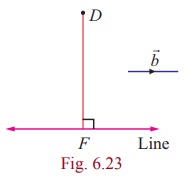
Since ![]() is perpendicular to
is perpendicular to ![]() ,
we have
,
we have
![]() .
. ![]() = 0 ⇒ 2(2t + 2) + 3(3t - 6) +1(t) = 0
= 0 ⇒ 2(2t + 2) + 3(3t - 6) +1(t) = 0
⇒ t = 1
Therefore, the coordinate of F is (3,-1, 4)
Now, the perpendicular distance from the given point to the given
line is
DF = | ![]() |= √[42+(-3)2+12]
= √26 units.
|= √[42+(-3)2+12]
= √26 units.
Equation of a plane when a normal to the plane and the distance
of the plane from the origin are given
(a) Vector equation of a plane in normal form
Theorem 1 :
The equation of the plane at a distance p from
the origin and perpendicular to the unit normal vector d is ![]() ⋅ d = p .
⋅ d = p .
Proof
Consider a plane whose perpendicular distance from the origin
is p .
Let A be the foot of the perpendicular from to
the plane.
Let d be the unit normal vector in the direction of ![]() .
.
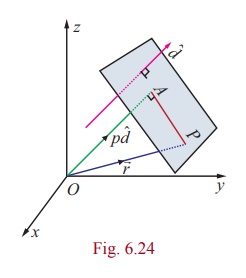
Then ![]() = pd .
= pd .
If ![]() is the position vector of
an arbitrary point P on the plane,
is the position vector of
an arbitrary point P on the plane,
then ![]() is perpendicular to
is perpendicular to ![]() .
.
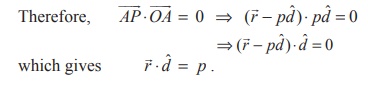
The above equation is called the vector equation of the plane
in normal form.
(b) Cartesian equation of a plane in normal form
Let l, m, n be the
direction cosines of d. Then we have d = li
+ mj + nk.
Thus, equation (1) becomes
![]() . (li + mj + nk) = p
. (li + mj + nk) = p
If P is (x,y,z), then ![]() = xi + yj + zk
= xi + yj + zk
Therefore, (xi + yj + zk) ⋅ (li + mj + nk) = p or lx + my + nz = p
............(2)
Equation (2) is called the Cartesian equation of the plane
in normal form.
Equation of a plane perpendicular to a vector and passing
through a given point
(a) Vector form of equation
Consider a plane passing through a point A with
position vector ![]() and
and ![]() is a normal vector to the
given plane.
is a normal vector to the
given plane.
Let ![]() be the position vector of an arbitrary point P on
the plane.
be the position vector of an arbitrary point P on
the plane.
Then ![]() is perpendicular to
is perpendicular to ![]() .
.
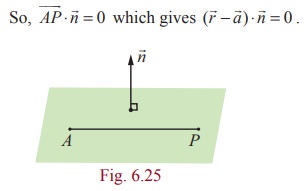
which is the vector form of
the equation of a plane passing through a point with position vector ![]() and perpendicular to
and perpendicular to ![]() .
.
(b) Cartesian form of equation
If a, b, c are the
direction ratios of ![]() ,
then we have
,
then we have ![]() = ai + bj + ck.
= ai + bj + ck.
Suppose, A is (x1 , y1 , z1)
then equation (1) becomes ((x − x1 )i + ( y − y1 )
j + (z − z1 )k) ⋅ (ai + bj + ck)
= 0 . That is,
a(x − x1) + b( y − y1)
+ c(z − z1) = 0
which is the Cartesian
equation of a plane, normal to a vector with direction ratios a, b, c and
passing through a given point (x1 , y1 , z1)
.
Intercept
form of the equation of a plane
Let
the plane ![]() ⋅
⋅ ![]() = q meets
the coordinate axes at A,B,C respectively
such that the intercepts on the axes are OA = a, OB = b, OC = c .
Now position vector of the point A is ai. Since A lies on the given
plane, we have ai⋅
= q meets
the coordinate axes at A,B,C respectively
such that the intercepts on the axes are OA = a, OB = b, OC = c .
Now position vector of the point A is ai. Since A lies on the given
plane, we have ai⋅ ![]() = q
which gives
= q
which gives ![]() .
.
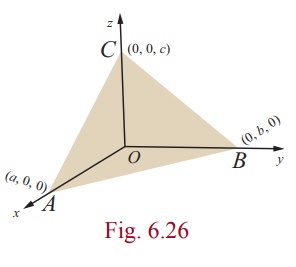
Similarly,
since the vectors bj and
ck lie
on the given plane, we have 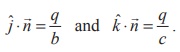 .
Substituting
.
Substituting ![]() = xi + yj + zk in
= xi + yj + zk in ![]() ⋅
⋅ ![]() =
q , we get
=
q , we get
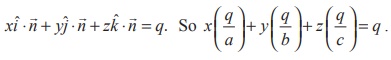
Dividing
by q, we get, 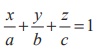 .
This is called the intercept form of equation of the plane
having intercepts a, b, c on the x, y, z axes respectively.
.
This is called the intercept form of equation of the plane
having intercepts a, b, c on the x, y, z axes respectively.
1.
The general equation ax + by + cz + d =
0 of first degree in x, y, z represents
a plane.
Proof
The
equation ax + by + cz + d = 0 can be
written in the vector form as follows
![]()
Since
this is the vector form of the equation of a plane in standard form, the given
equation ax + by + cz + d =
0 represents a plane. Here ![]() = ai
+ bj + ck. is
a vector normal to the plane.
= ai
+ bj + ck. is
a vector normal to the plane.
2.
Find the vector and Cartesian
form of the equations of a plane which is at a distance of 12 units from the
origin and perpendicular to 6i + 2 j − 3k .
Solution
Let ![]() =
6i + 2 j − 3k and P
=12.
=
6i + 2 j − 3k and P
=12.
If d
is the unit normal vector in the direction of the vector 6i + 2j −
3k , then
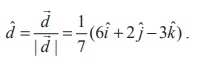
If ![]() is
the position vector of an arbitrary point (x, y, z) on the plane, then using
is
the position vector of an arbitrary point (x, y, z) on the plane, then using ![]() .
. ![]() =
p , the vector equation of the plane in normal form
is
=
p , the vector equation of the plane in normal form
is
![]()
Substituting ![]() = xi + yj + zk in the above equation, we
get (xi + yj + zk ) . 1/7 (6i
+ 2 j - 3k ) = 12 .
= xi + yj + zk in the above equation, we
get (xi + yj + zk ) . 1/7 (6i
+ 2 j - 3k ) = 12 .
Applying
dot product in the above equation and simplifying, we get 6x +
2 y − 3z = 84, which
is the the standard form.
3. If
the Cartesian equation of a plane is 3x - 4 y + 3z =
-8 , find the vector equation of the plane in the standard
form.
Solution
If ![]() = xi + yj + zk is
the position vector of an arbitrary point (x, y, z)
on the plane, then the given equation can be written as (xi + yj + zk) ⋅ (3i − 4 j +
3k) = −8 or (xi + yj + zk) ⋅ (−3i
+ 4 j − 3k) = 8 . That is,
= xi + yj + zk is
the position vector of an arbitrary point (x, y, z)
on the plane, then the given equation can be written as (xi + yj + zk) ⋅ (3i − 4 j +
3k) = −8 or (xi + yj + zk) ⋅ (−3i
+ 4 j − 3k) = 8 . That is, ![]() ⋅ (−3i +
4j − 3k ) = 8 which is
the vector equation of the given plane in standard form.
⋅ (−3i +
4j − 3k ) = 8 which is
the vector equation of the given plane in standard form.
4.
Find the direction cosines of
the normal to the plane and length of the perpendicular from the origin to the
plane ![]() ⋅ (3i −
4 j +12k ) = 5.
⋅ (3i −
4 j +12k ) = 5.
Solution
Let ![]() =
3i − 4 j +12k and q = 5 .
=
3i − 4 j +12k and q = 5 .
If d
is the unit vector in the direction of the vector 3i − 4 j +12k , then d = 1/13 (3i − 4 j +12k)
Now,
dividing the given equation by 13 , we get
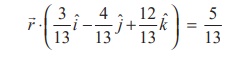
which is the equation of the plane in
the normal form ![]() .d = p
.d = p
From
this equation, we infer that 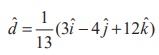 is
a unit vector normal to the plane from the origin. Therefore, the direction
cosines of d are
is
a unit vector normal to the plane from the origin. Therefore, the direction
cosines of d are 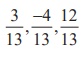 and
the length of the perpendicular from the origin to the plane is
5/13.
and
the length of the perpendicular from the origin to the plane is
5/13.
5.
Find the vector and Cartesian equations
of the plane passing through the point with position vector 4i + 2 j −
3k and normal to vector 2i − j + k .
Solution
If
the position vector of the given point is ![]() =
4i + 2 j − 3k and
=
4i + 2 j − 3k and ![]() =
2i − j + k , then the
equation of the plane passing through a point and normal to a vector is given
by (
=
2i − j + k , then the
equation of the plane passing through a point and normal to a vector is given
by (![]() −
− ![]() ) ⋅
) ⋅ ![]() =
0 or
=
0 or ![]() ⋅
⋅ ![]() =
= ![]() ⋅
⋅ ![]() .
.
Substituting ![]() =
4i + 2 j − 3k and
=
4i + 2 j − 3k and ![]() =
2i − j + k in the above equation, we get
=
2i − j + k in the above equation, we get
![]() = (4i +
2 j − 3k ). (2i − j + k )
= (4i +
2 j − 3k ). (2i − j + k )
Thus,
the required vector equation of the plane is ![]() ⋅(2i − j + k )
= 3 . If
⋅(2i − j + k )
= 3 . If ![]() = xi + yj + zk then
we get the Cartesian equation of the plane 2x − y + z =
3 .
= xi + yj + zk then
we get the Cartesian equation of the plane 2x − y + z =
3 .
6.
A variable plane moves in such
a way that the sum of the reciprocals of its intercepts on the coordinate
axes is a constant. Show that the plane passes through a fixed point
Solution
The
equation of the plane having intercepts a, b, c on
the x, y, z axes respectively is 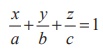 .
.
Since
the sum of the reciprocals of the intercepts on the coordinate axes is a
constant, we have 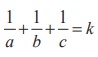 where k is
a constant, and which can be written as
where k is
a constant, and which can be written as 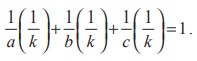
This
shows that the plane 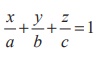 passes
through the fixed point
passes
through the fixed point 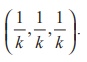
Equation of a plane passing
through three given non-collinear points
(a)
Parametric form of vector equation
1.
If three non-collinear points with position vectors ![]() ,
, ![]() ,
, ![]() are
given, then the vector equation of the plane passing through the given points
in parametric form is
are
given, then the vector equation of the plane passing through the given points
in parametric form is
![]()
Proof
Consider
a plane passing through three non-collinear points A, B, C with
position vectors ![]() ,
, ![]() ,
, ![]() respectively.
Then atleast two of them are non-zero vectors. Let us
take
respectively.
Then atleast two of them are non-zero vectors. Let us
take ![]() ≠
0 and
≠
0 and ![]() ≠
0 . Let
≠
0 . Let ![]() be the
position vector of an arbitrary point P on the plane. Take a
point D on AB (produced) such that
be the
position vector of an arbitrary point P on the plane. Take a
point D on AB (produced) such that ![]() is
parallel to
is
parallel to ![]() and
and ![]() is
parallel to
is
parallel to ![]() .
Therefore,
.
Therefore,
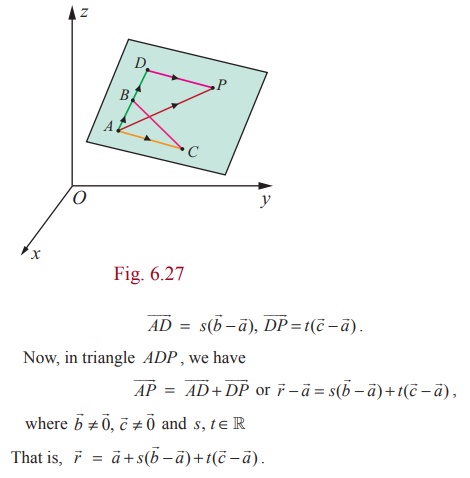
This
is the parametric form of vector equation of the plane passing through the
given three non-collinear points.
(b)
Non-parametric form of vector equation
Let A, B,
and C be the three non collinear points on the plane with position
vectors ![]() ,
, ![]() ,
, ![]() respectively.
Then atleast two of them are
non-zero vectors. Let us take
respectively.
Then atleast two of them are
non-zero vectors. Let us take ![]() ≠
0 and
≠
0 and ![]() ≠
0 .
≠
0 .
Now ![]() =
=![]() -
- ![]() and
and ![]() =
=![]() -
- ![]() .
The vectors (
.
The vectors ( ![]() -
- ![]() and
and ![]() -
- ![]() lie on the plane. Since
lie on the plane. Since ![]() ,
, ![]() ,
, ![]() are non-collinear,
are non-collinear, ![]() is not parallel to
is not parallel to ![]() .
Therefore,
.
Therefore, ![]() is
perpendicular to the plane.
is
perpendicular to the plane.
If ![]() is
the position vector of an arbitrary point P(x, y, z)
on the plane, then the equation of the plane passing through
the point A with position vector
is
the position vector of an arbitrary point P(x, y, z)
on the plane, then the equation of the plane passing through
the point A with position vector ![]() and
perpendicular to the vector
and
perpendicular to the vector ![]() is
given by
is
given by
![]()
This
is the non-parametric form of vector equation of the plane passing through
three non-collinear points.
(c)
Cartesian form of equation
If
(x1 , y1 , z1 ),
(x2 , y2 , z2 )
and (x3 , y3 , z3 )
are the coordinates of three non-collinear points A, B, C with
position vectors ![]() ,
, ![]() ,
, ![]() respectively
and (x, y, z) is the coordinates of the
point P with position vector
respectively
and (x, y, z) is the coordinates of the
point P with position vector ![]() , then we have
, then we have
![]()
Using
these vectors, the non-parametric form of vector equation of the plane passing
through the given three non-collinear points can be equivalently written as
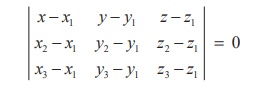
which
is the Cartesian equation of the plane passing through three non-collinear
points.
Condition
for a line to lie in a plane
We
observe that a straight line will lie in a plane if every point on the line,
lie in the plane and the normal to the plane is perpendicular to the line.
i) If the line ![]() lies
in the plane
lies
in the plane ![]() ⋅
⋅![]() = d , then
= d , then ![]() ⋅
⋅ ![]() = d
and
= d
and ![]() .
.![]() = 0
= 0
ii)
if the line 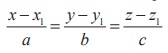 lies
in the plane Ax + By + Cz + D = 0 , then
lies
in the plane Ax + By + Cz + D = 0 , then
Ax1 + By1 + Cz1 + D =
0 and aA + bB + cC =
0
1.
Verify whether the line 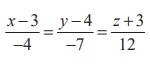 lies
in the plane 5x − y + z = 8 .
lies
in the plane 5x − y + z = 8 .
Solution
Here,
( x1, y1, z1 )
= (3, 4, −3) and direction ratios of the given straight line are (a,b, c) = (−4, −7,12)
. Direction ratios of the normal to the given plane
are ( A, B,C ) =
(5, −1,1) .
We
observe that, the given point ( x1, y1, z1 )
= (3, 4, −3) satisfies the given plane 5x − y + z =
8
Next, aA + bB + cC = (−4)(5)
+ (−7)(−1) + (12)(1) = −1 ≠ 0 . So, the normal to the
plane is not perpendicular to the line. Hence, the given line does not lie in
the plane.
Condition For Co Planarity Of Two Lines
(a) Condition in vector form
The two given non-parallel
lines ![]() are coplanar. So they lie in
a single plane. Let A and C be the points whose position vectors are
are coplanar. So they lie in
a single plane. Let A and C be the points whose position vectors are ![]() and
and ![]() .
Then A and C lie on the plane. Since
.
Then A and C lie on the plane. Since ![]() and
and ![]() are parallel to the plane,
are parallel to the plane, ![]() Χ
Χ ![]() is perpendicular to the
plane. So
is perpendicular to the
plane. So ![]() is perpendicular to
is perpendicular to ![]() Χ
Χ ![]() . That is,
. That is,
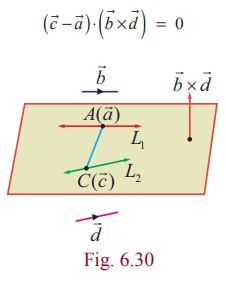
This is the required condition for coplanarity
of two lines in vector form.
(b) Condition in Cartesian form
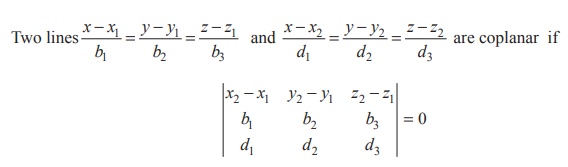
This is the required condition for coplanarity
of two lines in Cartesian form.
Equation
Of Plane Containing Two Non-Parallel Coplanar Lines
(a)
Parametric form of vector equation
Let ![]() be
two non-parallel coplanar lines. Then
be
two non-parallel coplanar lines. Then ![]() Χ
Χ ![]() ≠
≠ ![]() .
Let P be any point on the plane and let
.
Let P be any point on the plane and let ![]() 0 be
its position vector. Then, the vectors
0 be
its position vector. Then, the vectors ![]() are
also coplanar. So, we get
are
also coplanar. So, we get ![]() .
Hence, the vector equation in parametric
form is
.
Hence, the vector equation in parametric
form is ![]() .
.
(b)
Non-parametric form of vector equation
Let ![]() be
two non-parallel coplanar lines. Then
be
two non-parallel coplanar lines. Then ![]() Χ
Χ ![]() ≠
≠ ![]() .
Let P be any point on the plane and let
.
Let P be any point on the plane and let ![]() 0 be
its position vector. Then, the vectors
0 be
its position vector. Then, the vectors ![]() are
also coplanar. So, we get
are
also coplanar. So, we get ![]() .
Hence, the vector equation in non-parametric form is
.
Hence, the vector equation in non-parametric form is ![]() .
.
(C)
Cartesian form of equation of plane
In
Cartesian form the equation of the plane containing the two given coplanar
lines
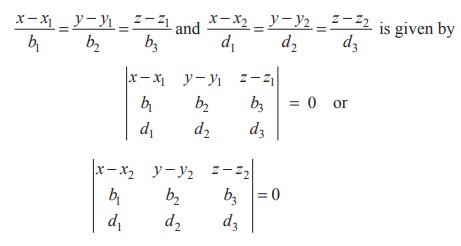
1. Show
that the lines 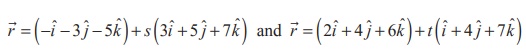 are
coplanar. Also,find the
non-parametric form of vector equation of the plane containing these lines.
are
coplanar. Also,find the
non-parametric form of vector equation of the plane containing these lines.
Solution
Comparing
the two given lines with
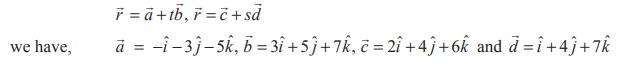
We
know that the two given lines are coplanar ,
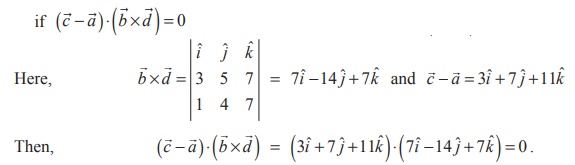
Therefore
the two given lines are coplanar.Then we find the non parametric form of vector equation of the plane
containing the two given coplanar lines. We know that the plane containing the
two given coplanar lines is
![]()
which
implies that (![]() -
(-i - 3j - 5k)).(7i
-14j + 7k) = 0 . Thus, the required non-parametric vector
equation of the plane containing the two given coplanar lines is
-
(-i - 3j - 5k)).(7i
-14j + 7k) = 0 . Thus, the required non-parametric vector
equation of the plane containing the two given coplanar lines is ![]() .
(i - 2j + k ) = 0.
.
(i - 2j + k ) = 0.
Angle
Between Two Planes :
The
angle between two given planes is same as the angle between their normals.
Proof
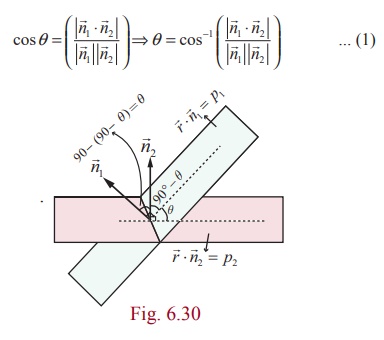
If θ is
the acute angle between two planes ![]() ⋅
⋅ ![]() 1 = p1 and
1 = p1 and ![]() ⋅
⋅![]() 2 = p2 ,
then θ is the acute angle between their normal vectors
2 = p2 ,
then θ is the acute angle between their normal vectors ![]() 1 and
1 and ![]() 2
2
Therefore,
1. The acute angle θ between
the planes a1x + b1y + c1z + d1 =
0 and a2x + b2y + c2z + d2 =
0 is given by
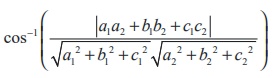
Proof
If ![]() 1 and
1 and ![]() 2 are
the vectors normal to the two given planes a1x + b1y +
c1z + d1 = 0 and a2x + b2y + c2z + d2 =
0 respectively. Then,
2 are
the vectors normal to the two given planes a1x + b1y +
c1z + d1 = 0 and a2x + b2y + c2z + d2 =
0 respectively. Then, ![]()
Therefore,
using equation (1) in theorem 6.18 the acute angle θ between the planes is
given by
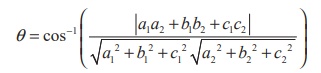
2. Find
the acute angle between the planes ![]() .(2
i + 2 j + 2k )
= 11 and 4x - 2 y + 2z = 15
.(2
i + 2 j + 2k )
= 11 and 4x - 2 y + 2z = 15
Solution
The
normal vectors of the two given planes ![]() =
(2 i + 2 j + 2k ) = 11 and 4x - 2 y + 2z = 15 are
=
(2 i + 2 j + 2k ) = 11 and 4x - 2 y + 2z = 15 are ![]() 1 =
2i + 2 j + 2k and
1 =
2i + 2 j + 2k and ![]() 2 =
4i - 2 j + 2k respectively.
2 =
4i - 2 j + 2k respectively.
If
θ is the acute angle between the planes, then we have
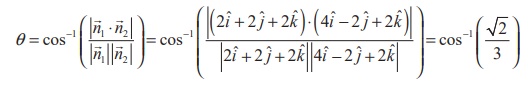
Angle Between A Line And A Plane
We know that the angle between a line and a plane is the complement of
the angle between the normal to the plane and the line
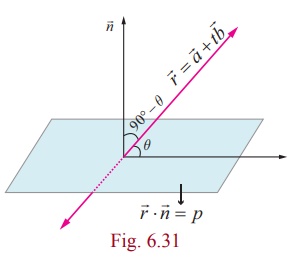
Let ![]() =
= ![]() + t
+ t![]() be the equation of the line and
be the equation of the line and ![]() ⋅
⋅ ![]() = p be the equation of the plane. We know that
= p be the equation of the plane. We know that ![]() is parallel to the given
line and
is parallel to the given
line and ![]() is normal to the given
plane. If θ is the acute angle between the line and the
plane, then the acute angle between
is normal to the given
plane. If θ is the acute angle between the line and the
plane, then the acute angle between ![]() and
and ![]() is
((π/2)-θ).Therefore,
is
((π/2)-θ).Therefore,
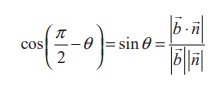
So, the acute angle between the line and the plane is given by
θ = 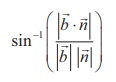 .(1)
.(1)
In Cartesian form if 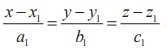 and ax + by + cz = p are the equations of
the line and the plane, then
and ax + by + cz = p are the equations of
the line and the plane, then ![]() = a1i + b1 j +
c1k and
= a1i + b1 j +
c1k and ![]() = ai + bj + ck . Therefore, using (1), the acute angle θ between
the line and plane is given by
= ai + bj + ck . Therefore, using (1), the acute angle θ between
the line and plane is given by
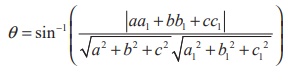
1. Find the angle between the straight line ![]() = (2i + 3j + k )+ t (i - j + k ) and the
plane 2x - y + z = 5 .
= (2i + 3j + k )+ t (i - j + k ) and the
plane 2x - y + z = 5 .
Solution
The angle between a line ![]() =
= ![]() + t
+ t![]() and a plane
and a plane ![]() ⋅
⋅ ![]() = p with normal
= p with normal ![]() is θ
is θ
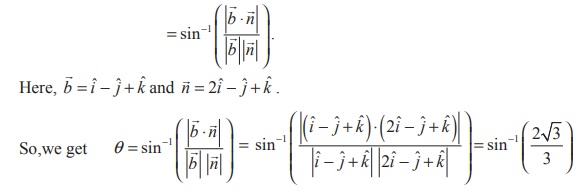
Distance
Of A Point From A Plane
(a)
Vector form of equation
1. The perpendicular distance from a point with
position vector ![]() to
the plane
to
the plane ![]() ⋅
⋅ ![]() = p is
given by
= p is
given by
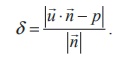
Proof
Let A be
the point whose position vector is ![]() .
.
Let F be
the foot of the perpendicular from the point A to the plane ![]() ⋅
⋅![]() = p .
The line joining F and A is parallel to the
normal vector
= p .
The line joining F and A is parallel to the
normal vector ![]() and
hence its equation is
and
hence its equation is ![]() =
= ![]() + t
+ t![]() .
.
But
F is the point of intersection of the line ![]() =
= ![]() +
t
+
t![]() and
the given plane
and
the given plane ![]() ⋅
⋅ ![]() = p . If
= p . If ![]() 1 is
the position vector of F, then
1 is
the position vector of F, then ![]() for
some t1 ∈ R, and
for
some t1 ∈ R, and ![]() ⋅
⋅ ![]() = p Eliminating
= p Eliminating ![]() 1 we
get
1 we
get
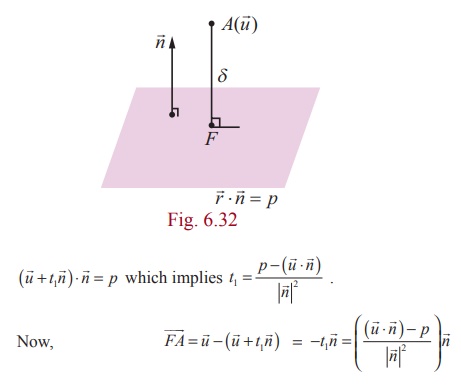
Therefore,
the length of the perpendicular from the point A to the given plane is
The
position vector of the foot F of the perpendicular AF is given by
(b) Cartesian form of equation
In
Caretesian form if A( x1 , y1 , z1 )
is the given point with position vector ![]() and ax + by + cz = p is the Cartesian
equation of the given plane, then
and ax + by + cz = p is the Cartesian
equation of the given plane, then ![]() = x1i
+ y1 j + z1k and
n = ai
+ bj + ck. Therefore, using these vectors
in
= x1i
+ y1 j + z1k and
n = ai
+ bj + ck. Therefore, using these vectors
in  we
get the perpendicular distance from a point to the plane in Cartesian form as
we
get the perpendicular distance from a point to the plane in Cartesian form as
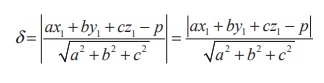
2.
Find the distance of a point
(2, 5, −3) from the plane ![]() ⋅ (6i −
3j + 2k ) = 5 .
⋅ (6i −
3j + 2k ) = 5 .
Solution
Comparing
the given equation of the plane with ![]() ⋅
⋅![]() = p we
have
= p we
have ![]() = 6i − 3j + 2k
= 6i − 3j + 2k
We
know that the perpendicular distance from the given point with position
vector ![]() to
the planer
to
the planer ![]() ⋅
⋅![]() = p is
given by
= p is
given by 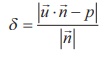 .Therefore, substituting
.Therefore, substituting ![]() in
the formula, we get
in
the formula, we get
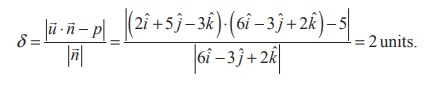
Distance
between two parallel planes
1. The
distance between two parallel planes ax + by + cz + d1 = 0
and ax + by + cz + d2 =
0 is given by
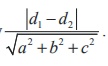
Proof
Let
A( x1 , y1 , z1 )
be any point on the plane ax + by + cz + d2 = 0
, then we have
ax1 + by1 + cz1 + d2 =
0 ⇒ ax1 + by1 + cz1 =
−d2
The
distance of the plane ax + by + cz + d1 = 0
from the point A( x1 , y1 , z1 )
is given by
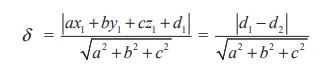
Hence,
the distance between two parallel planes ax + by + cz
+ d1 = 0 and ax + by + cz
+ d2 = 0 given by δ = 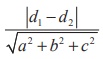 .
.
2. Find
the distance between the parallel planes x + 2 y −
2z +1 = 0 and 2x + 4 y − 4z +
5 = 0
Solution
We
know that the formula for the distance between two parallel planes ax + by + cz + d1 =
0 and ax + by + cz + d2 =
0 is 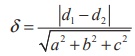 Rewrite
the second equation as x + 2y 2z +
5/2 = 0. Comparing the given equations with the general equations, we get a =
1, b = 2, c = −2, d1=1, d2 =
5/2.
Rewrite
the second equation as x + 2y 2z +
5/2 = 0. Comparing the given equations with the general equations, we get a =
1, b = 2, c = −2, d1=1, d2 =
5/2.
Substituting
these values in the formula, we get the distance
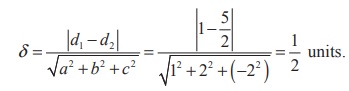
3. Find
the distance between the planes ⋅
![]()
Solution
Let ![]() be
the position vector of an arbitrary point on the plane
be
the position vector of an arbitrary point on the plane ![]() ⋅(2 i −
j − 2 k )
= 6 . Then, we have
⋅(2 i −
j − 2 k )
= 6 . Then, we have
![]() ⋅(2 i −
j − 2 k )
= 6
.................(1)
⋅(2 i −
j − 2 k )
= 6
.................(1)
If δ is
the distance between the given planes, then δ is the
perpendicular distance from ![]() to
the plane
to
the plane
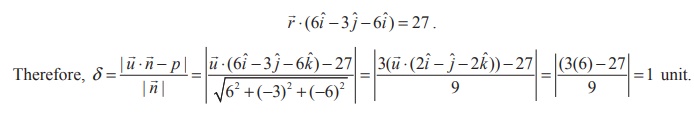
Equation Of Line Of Intersection Of Two Planes
:
Let ![]() ⋅
⋅![]() = p and
= p and ![]() ⋅
⋅![]() = q
be two non-parallel planes. We know that
= q
be two non-parallel planes. We know that ![]() and
and ![]() are perpendicular to the given planes respectively.
are perpendicular to the given planes respectively.
So, the line of intersection of
these planes is perpendicular to both ![]() Χ
Χ ![]()
![]() and
and ![]() . Therefore, it is parallel
to the vector
. Therefore, it is parallel
to the vector ![]() Χ
Χ ![]() . Let
. Let
![]()
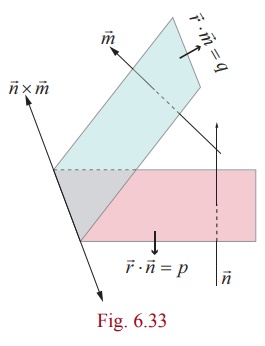
Consider the equations of two planes a1x + b1y + c1z = p
and a2x + b2y + c2z = q . The line of intersection of the two given
planes intersects atleast one of the coordinate
planes. For simplicity, we assume that the line meets the coordinate plane z =
0 . Substitute z=0 and obtain the two equations a1x + b1y − p =
0 and a2 x + b2y − q =
0 .Then by solving these equations, we get the values of x and y as x1 and y1 respectively.
So, ( x1 , y1 ,
0) is a point on the required line, which is parallel to l1i
+ l2 j + l3k
. So, the equation of the line is
Meeting
Point Of A Line And A Plane
1. The
position vector of the point of intersection of the straight line ![]() and
the plane
and
the plane
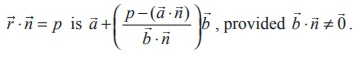
Proof
Let ![]() be
the equation of the given line which is not parallel to the given plane whose
equation is
be
the equation of the given line which is not parallel to the given plane whose
equation is
![]()
Let ![]() be
the position vector of the meeting point of the line with the plane. Then
be
the position vector of the meeting point of the line with the plane. Then ![]() satisfies
both
satisfies
both ![]() and
and ![]() ⋅
⋅![]() = p for
some value of t , say t1.
So, We get
= p for
some value of t , say t1.
So, We get
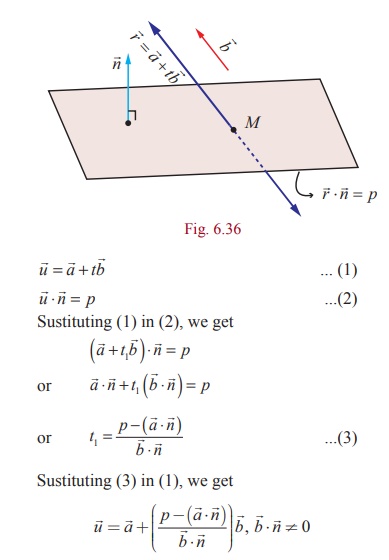
2.
Find
the coordinates of the point where the straight line ![]() intersects
the plane x − y + z −
5 = 0 .
intersects
the plane x − y + z −
5 = 0 .
Solution
![]()
The
vector form of the given plane is ![]()
We
know that the position vector of the point of intersection of the line ![]() and
the plane
and
the plane
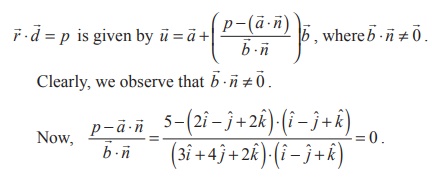
Therefore,the
position vector of the point of intersection of the given line and the given
plane is
![]()
That
is, the given straight line intersects the plane at the point (2, −1, 2 ).
