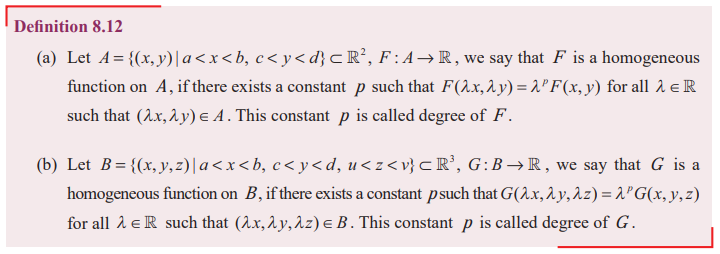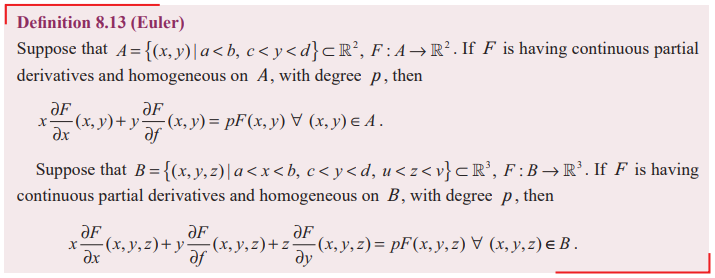Differentials and Partial Derivatives

Linear Approximation and Differentials

Linear Approximation

Using the linear approximation, we shall estimate the function value near a chosen point. Then we shall introduce differential of a real-valued function of one variable, which is also useful in applications.

Errors: Absolute Error, Relative Error, and Percentage Error

So the second approximation is a better approximation than the first one. Note that, in order to calculate the relative error or the percentage error one should know the actual value of what we are approximating.

Differentials

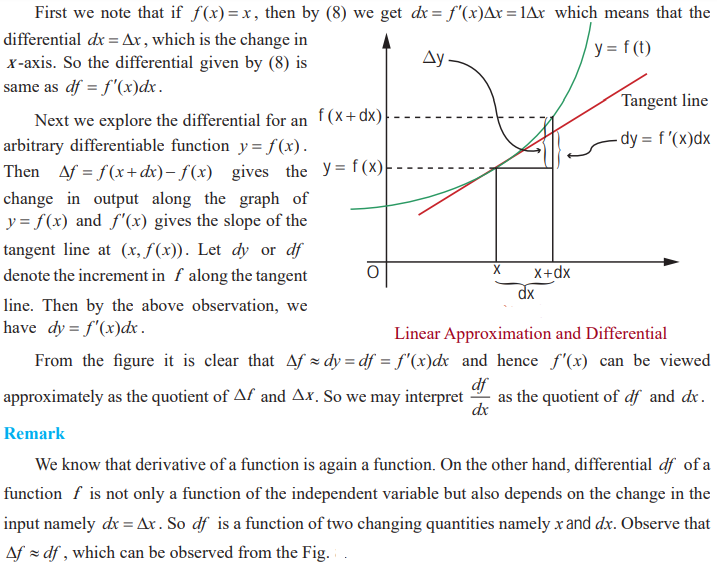
We use the derivative concept to introduce “Differential”. Let us take another look at (1),

Functions of several Variables

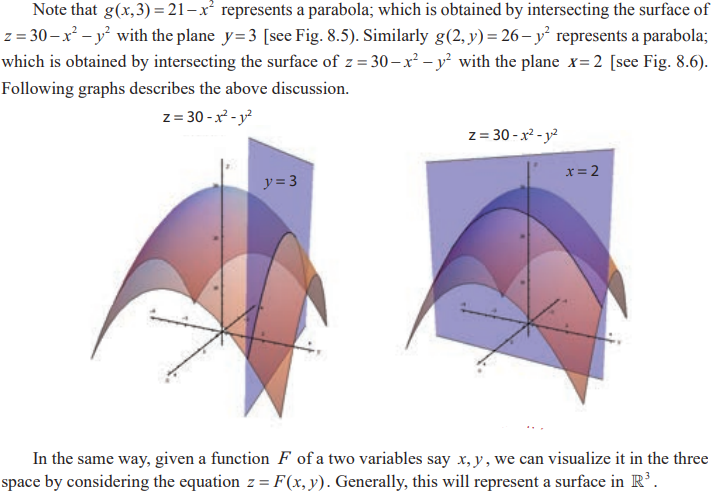
Recall of Limit and Continuity of Functions of One Variable

The above condition in terms of neighbourhoods can also be equivalently stated using modulus (or absolute value) notation as follows:

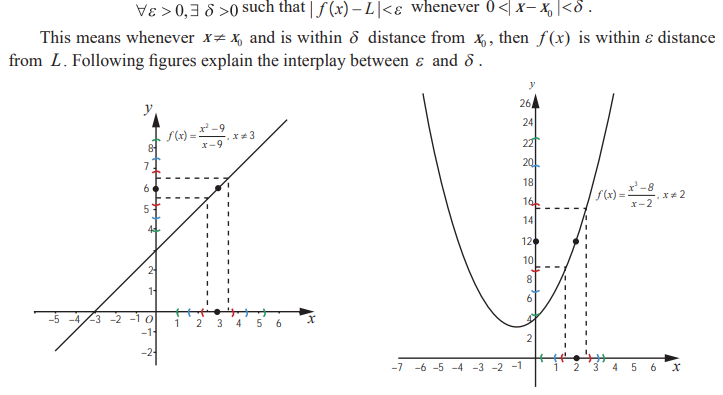
We also know, that a function f defined in the neighbourhood of x₀ except possibly at x₀ has a limit at x₀ if the following hold :

Limit and Continuity of Functions of Two Variables

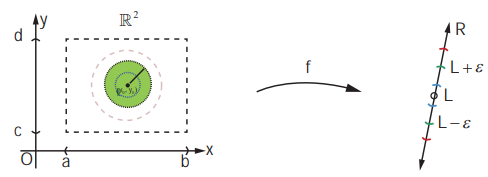
Limit of a function

When compared to the case of a function of single variable, for a function of two variables, there is a subtle depth in the limiting process. Here the values of F ( x, y) should approach the same value L , as ( x, y) approaches ( u, v) along every possible path to ( u, v) (including paths that are not straight lines). Figure explains the limiting process.

All the rules for limits (limit theorems) for functions of one variable also hold true for functions of several variables.

Now, following the idea of continuity for functions of one variable, we define continuity of a function of two variables.

Partial Derivatives

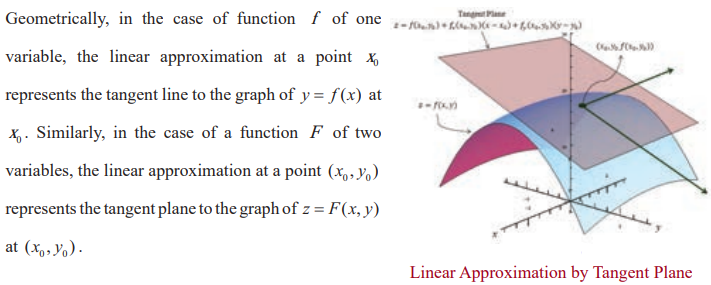
Linear Approximation and Differential of a function of several variables

Here we introduce similar ideas for functions of two variables and three variables. In general for functions of several variables these concepts can be defined similarly.

Here we shall outline the linear approximations and differential for the functions of three variables. Actually, we can define linear approximations and differential for real valued function having more variables, but we restrict ourselves to only three variables.

Function of Function Rule

Homogeneous Functions and Euler’s Theorem