Geometry

 

4.1 Introduction

➢      Geometry means the measurement of the earth. It includes the study of the properties of shapes and its measures.  In ancient days, geometry was developed for the practical purpose of construction, surveying and various crafts. Vehicles like cycle, car, and bus are designed using geometrical concepts.

 

➢      The toys that you play with, the tools like pencil, scale and book that you use with, give rise to geometrical ideas and shapes. In this chapter, we will learn about the geometrical concepts such as lines, line segments, rays and angles.

 

 

 

 

4.2 Fun with lines

 

            What shapes can you draw with 3 lines or 4 lines or 5 lines? We have already seen some shapes with names like triangles, rectangles and squares.

 

     

 

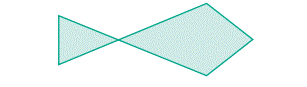
Here is a shape which is in the form of a fish (see Fig. 4.1). It has 5 lines. Can you draw a fish with 4 lines or with 3 lines? Think!

 

4.2.1 Only two lines

 

            What shapes can you draw with only TWO lines? The following forms are possible with 2 lines. Isn’t it?

 

 

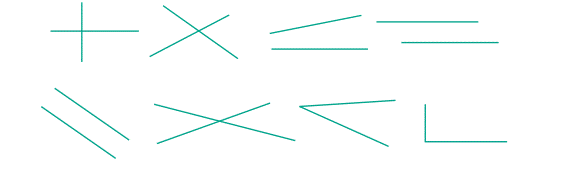
            Is there something you notice in all these shapes?

 

4.2.2 Only one line

 

            In Mathematics, every thinking is interesting and unlimited. Remember numbers; it is not stopped with adding 2 – digits. Numbers go on endlessly and it is possible to add any two numbers, however large. We know that even a 37- digit number ending in 0 is divisible by 5.

 

             It is the same with shapes too. We are interested in lines, triangles, rectangles and in whatever the shapes may be and the size however large or small. We need to give them names not only to describe them but also to explore a lot with them.

 

4.3 Describing lines

 

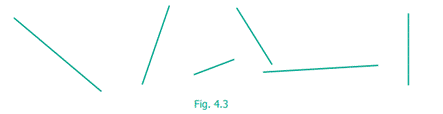
             A line can be long or short. A line can be flat or slant or vertical. If a line is rotated in any direction, it remains to be a line. So, given below (Fig. 4.3) are lines in different positions.

 

 

 

 

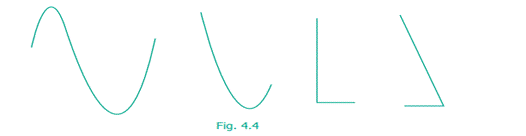
            But the following (Fig.4.4) are not lines

 

 

 

If the length of a line is ignored, then it can be extended in both the directions without ending as in (Fig. 4.5) given below. A line through two points A and B is written as AB or BA. Also it is denoted by a letter ‘ l ’

 

 

 

4.4 Line segment

 

            What do we call a line that is short and ends on both sides? That we call it as a line segment and name both of its ends with letters as shown in fig. 4.6.

 

 

            We usually use CAPITAL LETTERS to denote the ends of the line segments. A line segment is denoted by AB. What can we do with a line segment? We can measure its length. Given two line segments, we can compare their lengths and say which is shorter and which is longer.

 

            Even if we measure length as a number, we get lots of line segments, each with a definite length. Using a ruler, we can draw the following line segments.

 

 

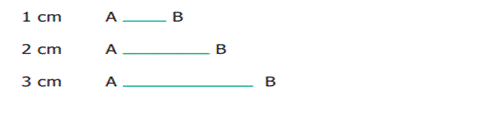
What about a line segment of length 17 cm or 20 cm or 30 cm or 378 cm? Like, numbers never end, line segments get longer and longer forever!

 

4.4.1 Construction of line segment

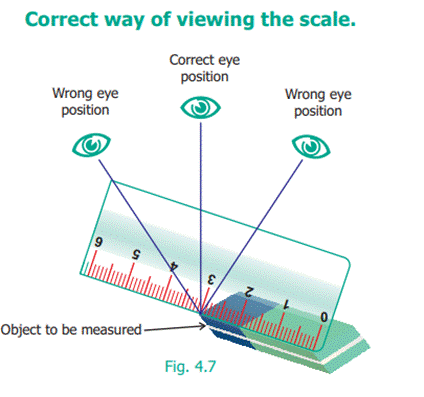
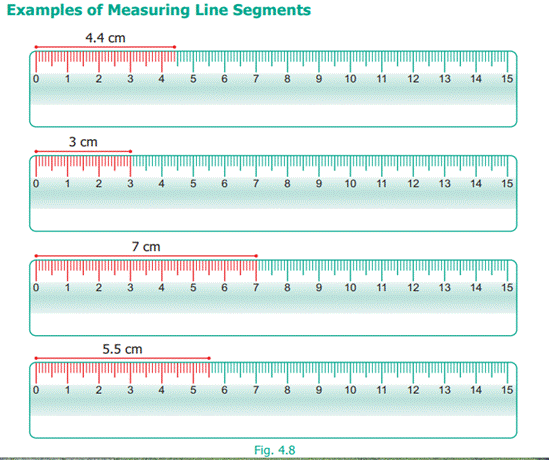
            Learn to measure line segments using the ruler

 

 

 

Example: 

            With the help of a ruler and compass, draw a line segment PQ = 5.5cm.

 

Solution:

● Draw a line ‘ l ’ and mark a point ‘P’ on it as shown in Fig. 4.10.

 

 

 

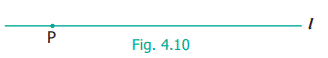
 ● Measure 5.5 cm using compass as shown in Fig. 4.11 placing the pointer at ‘0’ and the pencil pointer at 5.5 cm.

 

 

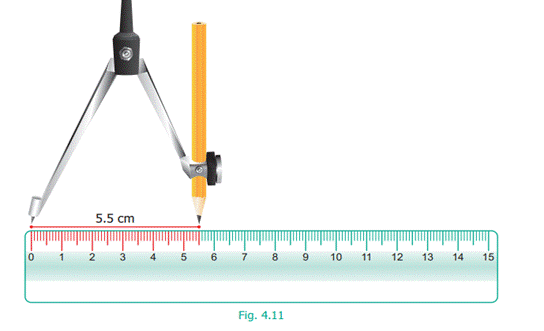
● Place the pointer of the compass at ‘ P ’ then draw a small arc on the line ‘l ’ with the pencil pointer (Fig. 4.12). It cuts the line ‘ l ’ at a point and name that point as ‘Q’ (Fig. 4.13).

 

 

 

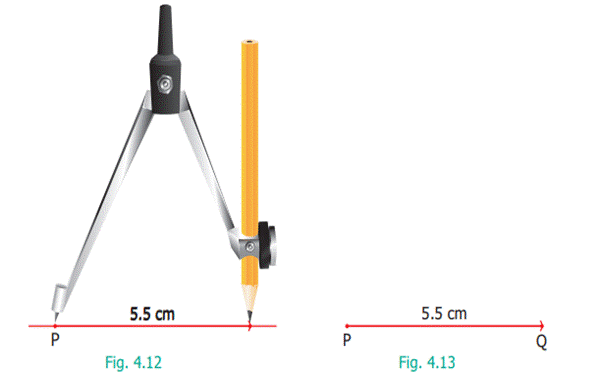
 ● Now, PQ is the required line segment of length 5.5 cm.

 

 

4.5 Two lines

 

            Now let us get back to two lines (Fig. 4.2). Lines that go on forever on either side without meeting each other (i.e. they have a constant distance in between) are called parallel lines.

 

            Thus, parallel lines go forever without meeting. What will happen if two lines are not parallel? Then they must meet somewhere! Of course, they go their way after meeting too.

 

 

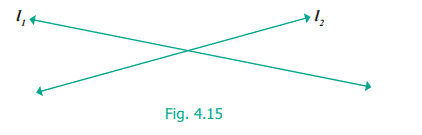
Here, are called intersecting lines. Of course, we now have parallel line segments and intersecting line segments too.

 

 

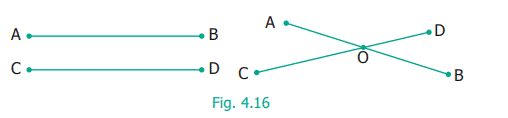
The position ‘O’ at which the line segments AB and CD meet is called their point of intersection.

 

 

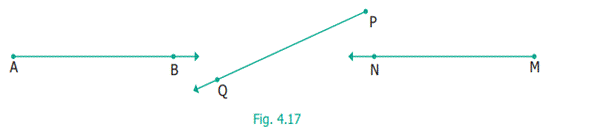
4.6 Rays

 

            What about lines that end on one side but proceed indefinitely on the other side? We call them rays. They are denoted by AB, PQ, MN..., etc. The fixed end point of a ray is called the starting point. (See fig.4.17)

 

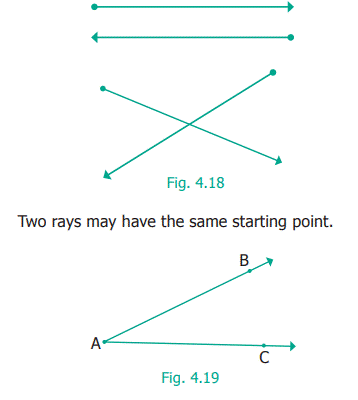
4.6.1 Two rays

 

With two rays we have more to learn. They can be parallel or intersecting.

 

 

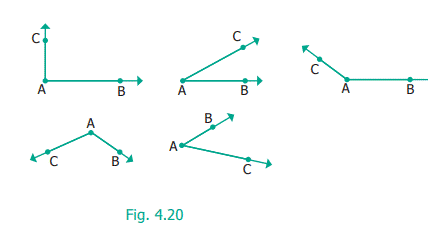
4.7 Angles

            Can we find a way to describe all these shapes? (Shown in fi g. 4.20)

 

 

When two rays or line segments meet at their end points, they form an angle at that point.

 

 

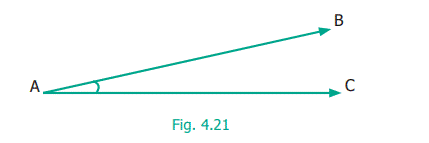
 In the Fig.4.21 rays and are the sides and ‘A’ is the vertex which is the meeting point of both the line segments.

 

4.7.1 Naming Angles

            We name the angle as shown in the Fig.4.22 below.

 

 

 

 

4.7.2 Measuring Angles

 

            Can we measure angles too? Yes, they are measured in degrees and denoted by the symbol ‘ Ί ’. This has to be marked at top right of a number. We write angles as 35°, 78°, 90°, 110°, and 145° and so on.

 

 

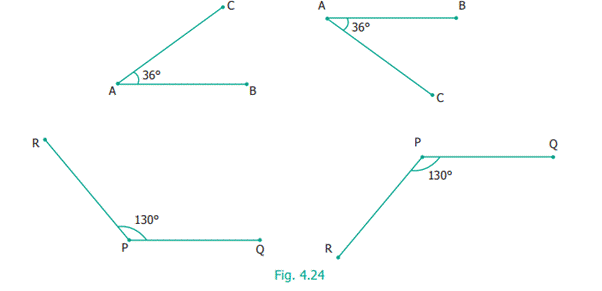
See that angles can be equal even if they are positioned differently.

 

 

4.7.3 Special Angles

             Some angles are special. 90° is one such. We call it as the right angle.

 

 

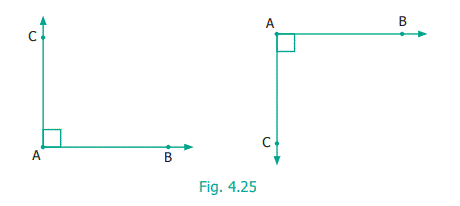
Right angle is most common in life. Examples can be seen at cross-roads, chess board, TV, etc.

 

 

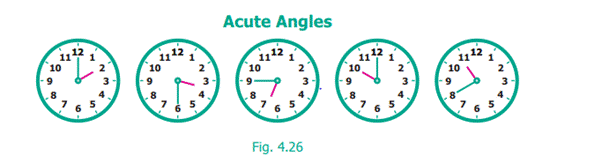
Each of the angles in the above Fig. 4.26 is less than a right angle. Angles smaller than 90Ί are called acute angles

 

 

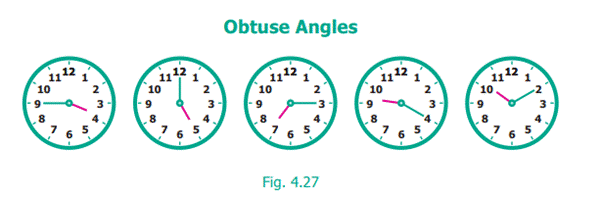
Each of the angles in the above Fig. 4.27 is greater than right angle. Angles more than 90Ί are called Obtuse angles.

 

4.8 Angle measurement using Protractor

How do we measure an angle? Using a Protractor we can measure an angle.

 

 

 

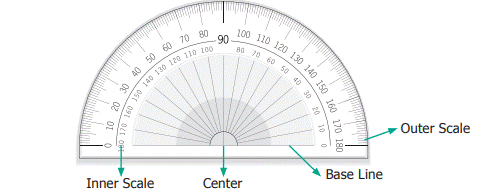
            A protractor has one center and a base line. It has two scales namely, inner scale from 0° to 180° in one direction and outer scale from 0° to 180° in the opposite direction. Why does the protractor stop with 180°? We can rotate the protractor and measure, so 180° is enough.

 

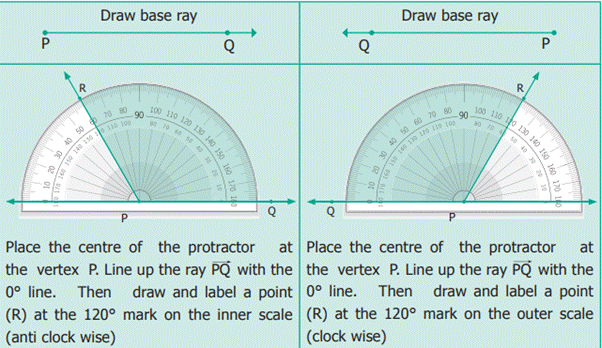
Steps to Measure an angle

 

 Step 1: Place the center of the protractor on the vertex of the angle and line up the base line with 0°.

 Step 2: Read the measure where the other ray crosses the protractor

 

 

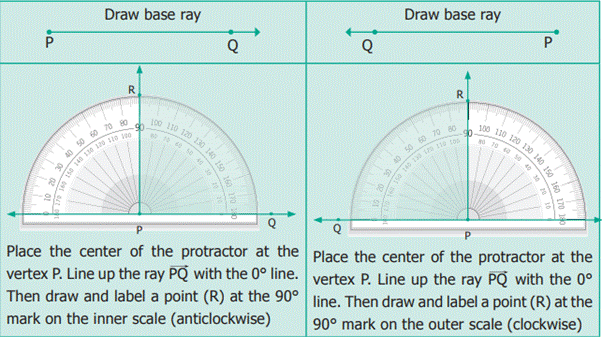
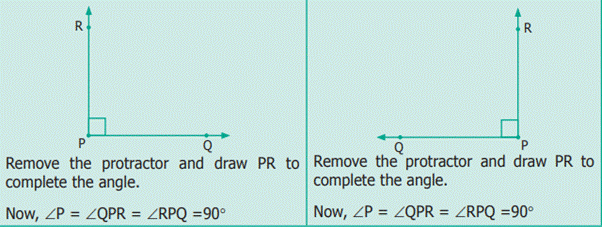
4.8.1 Using a Protractor to draw Right Angle (90Ί)

 

Example Use a Protractor to draw an angle 90Ί

 

 

 

 

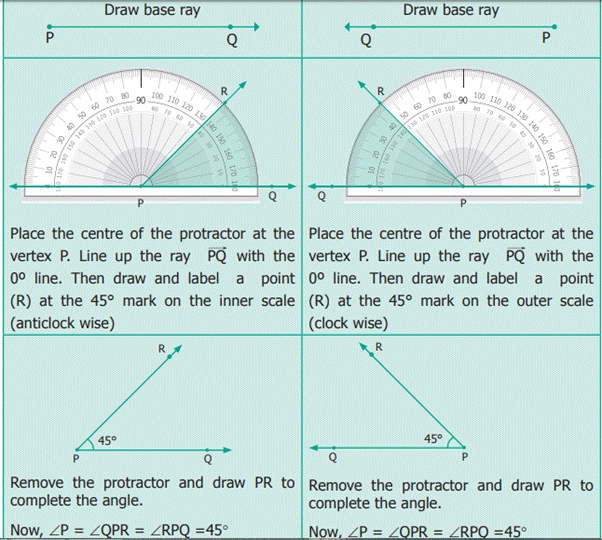
4.8.2 Using Protractor to draw an Acute Angle

 

Example: Use a Protractor to draw an angle 45°.

 

 

 

4.8.3 Using a Protractor to draw an Obtuse Angle

 

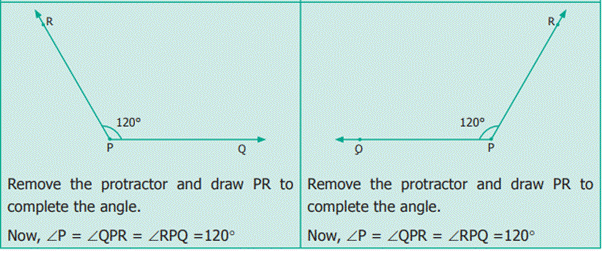
Example: Use a protractor to draw an obtuse angle 120°.

 

 

 

 

 

 

 

 

 

4.11 Points and lines

            When we have a line, we can mark a point on the line or not on it.

 

 

 

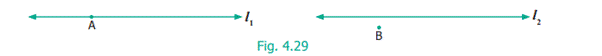
➢      . ‘B’ may be closer or far away, but not on the both of the lines ’. However, when any two points are given, there is exactly ONE line passing through them! Take several pairs of points and verify if this is true

 

➢      What about 3 points and a line? Consider the following lines be three points.

 

 

 

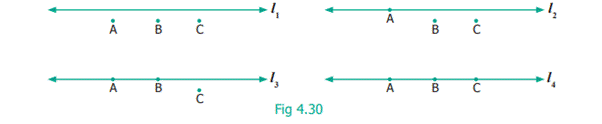
 When all the three points are on a line, they are special; we call such points as collinear points.

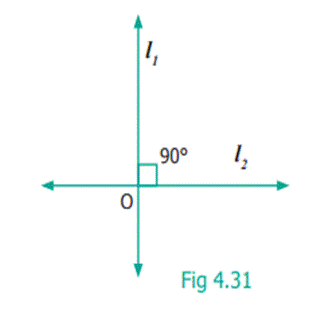
 When two lines intersect at right angles (90°), we call them as perpendicular lines. (Refer to 4.31)

 

 

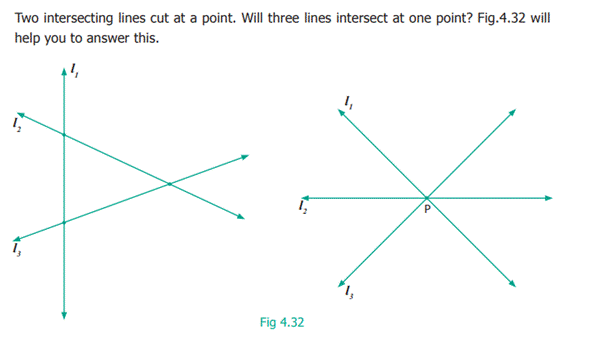
When many lines intersect at a single point, that is again special, we call that point P as a point of concurrency. The lines are called concurrent lines.