Geometry
4.1 Introduction
A closed
figure formed by three line segments is called a triangle
4.2 Basic Elements of a Triangle
● This
forms a triangle ABC represented as 
ABC or ∆BCA
or ∆CAB.
● In ∆ ABC,
the line segments AB, BC and CA are called the sides of the triangle and 
CAB,
ABC
and BCA
(A,
B
& C)
are called the angles of the triangle. The point of intersection of two sides
of the triangle is called the vertex.
● A, B and C are
three vertices of ∆ ABC. Hence, a triangle has 3 sides, 3 angles and 3
vertices.
4.3 Types and Properties of Triangles
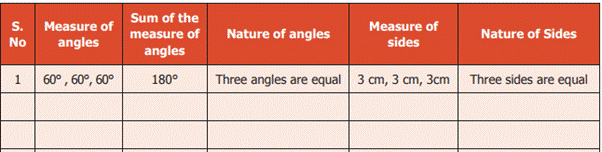
From the table, we observe the
following:
In
a triangle,
1. If
the measure of all angles are different, then all sides are different.
2. If
the measure of two angles are equal, then two sides are equal.
3. If
the measure of three angles are equal, then three sides are equal and each
angle measures 60°
4. Sum
of three angles of a triangle is 180°
4.3.1 Types of triangle based on its sides
i)
If three sides of a triangle are
different in lengths, then it is called a Scalene Triangle
Examples:
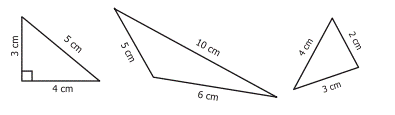
ii) If any two sides of a triangle are equal in length, then
it is called an Isosceles Triangle
Examples:
iii)
If three sides of a triangle are equal
in length, then it is called an Equilateral Triangle
Examples:
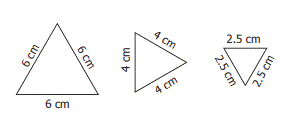
Thus, based on the sides of triangles, we can classify
triangles into 3 types.
4.3.2 Types of triangle based on its
angles
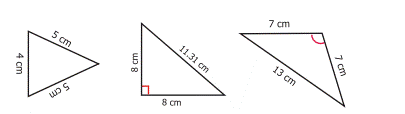
i)
If three angles of a triangle are acute
angles (between 0° and 90°), then it is called an Acute Angled Triangle.
Examples:
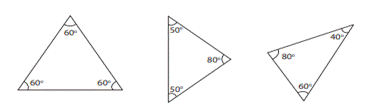
ii) If
an angle of a triangle is a right angle (90°), then it is called a Right Angled
Triangle.
Examples:
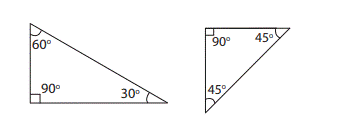
iii)
If an angle of a triangle is an obtuse
angle (between 90°and 180°), then it is called an Obtuse Angled Triangle.
Examples:
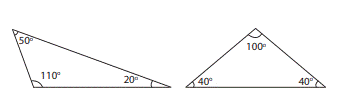
Thus, based on the
angles of triangles, we can classify triangles into 3 types.
4.3.3 Triangle Inequality property
In a triangle, the sum of any two sides of a triangle is
greater than the third side. This is known as Triangle Inequality property.
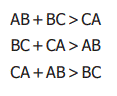
Example 1: Can a triangle be
formed with 7 cm, 10 cm and 5 cm as its sides"
Solution:
Instead of checking triangle inequality
by all the sides in the triangle, check only with two smaller sides.
Sum of two smaller sides of the triangle =
5+7=12 cm >10 cm, the third side.
It is greater than the third side. So, a
triangle can be formed with the given sides.
Example 2:
Can
a triangle be formed with 7 cm, 7 cm and 7 cm as its sides
Solution:
If three sides are equal, then
definitely a triangle can be formed, as the triangle inequality is satisfied.
Example 3: Can a triangle be
formed with 8 cm, 3 cm and 4 cm as its sides"
Solution:
The
sum of two smaller sides = 3+4=7 cm < 8 cm, the third side.
It
is less than the third side.
So,
a triangle cannot be formed with the given sides.
Example 4: Can a triangle be
formed with the angles 80°, 30°, 40°"
Solution:
The sum of three angles = 80+ 30+ 40 =
150° (not equal to 180°) in a triangle, the sum of three angles is 180.
So,
a triangle cannot be formed with the given angles.
4.4 Construction of Perpendicular Lines
4.4.1 Introduction
In
Geometry, to measure the height of figures, we use perpendicular lines
4.4.2 Set Squares
The
set squares are two triangle shaped instruments in the Geometry Box. Each of
them has a right angle. One set square has the angles 30°, 60°, 90° and the
other set square has the angles 45°, 45°, 90°. The perpendicular edges are
graduated in centimeters.
Set squares have several uses:
• To construct the specific angles 30°,
45°, 60°, 90°
• To draw parallel and perpendicular
lines
• To measure the height of the shapes
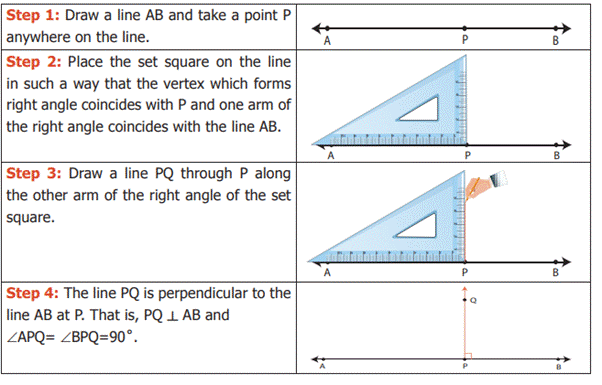
Example 5:
Construct a
line perpendicular to the given line at a point on the line.
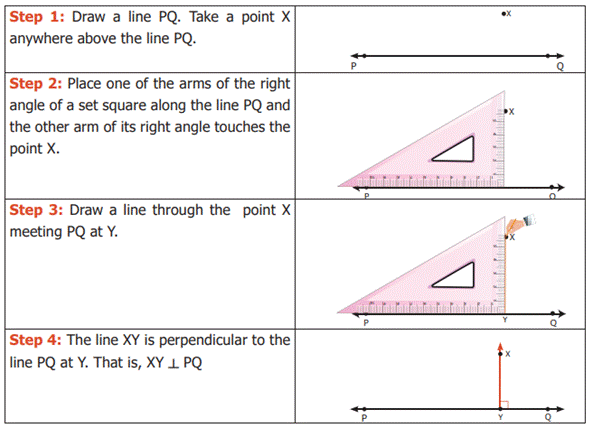
Example 6: Construct a line
perpendicular to the given line through a point above it.
4.5 Construction of Parallel Lines
1.
Place a scale on a paper and draw lines
along both the edges of the scale as shown.
2.
Place the set square at two different
points on 
and
find the distance between
and
Are
they equal? Yes.
3.
Thus, the perpendicular distance
between a set of parallel lines remains the same.
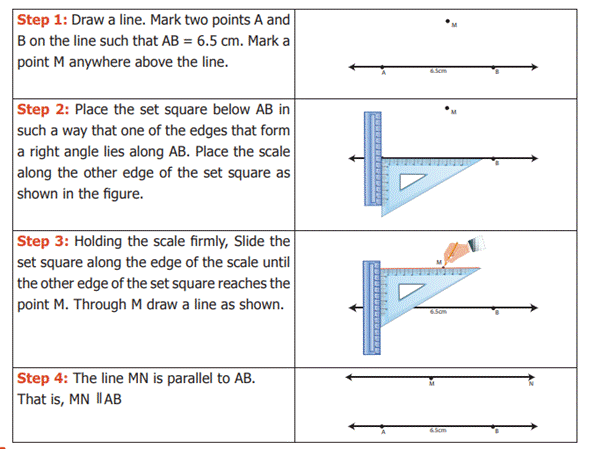
Example 7: Draw a line segment AB = 6.5 cm and
mark a point M above it. Through M draw a line parallel to AB.
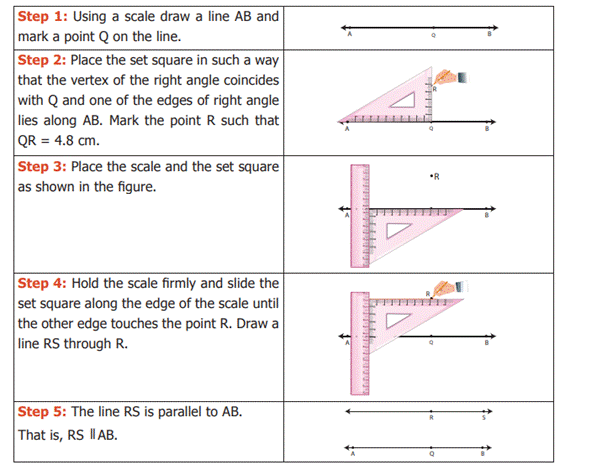
Example 8: Draw a line and mark a point R at a
distance of 4.8 cm above the line. Through R draw a line parallel to the given
line.
Example 9:
Draw
a line segment PQ = 12 cm. Mark two points M, N at a distance of 5 cm above the
line segment PQ. Through M and N draw a line parallel to PQ.
