Information Processing
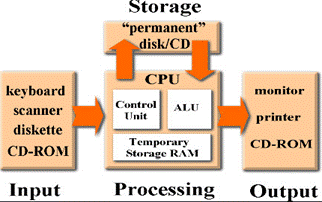
5.1 Introduction
Computers
use Tree diagram to perform billions of operations in a uniform way and gives
the answer. We will learn about the Tree diagram for both numeric and algebraic
expressions in this chapter.
Consider the numerical expression [(9 –
4) X 8] ÷ [(8 + 2) X 3]. We can try to understand the expression in a better
way through the tree diagram.
1)
Let us consider e1 = (9 – 4) X 8, e2 = (8 + 2) X 3 we get
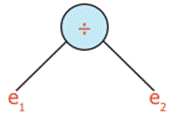
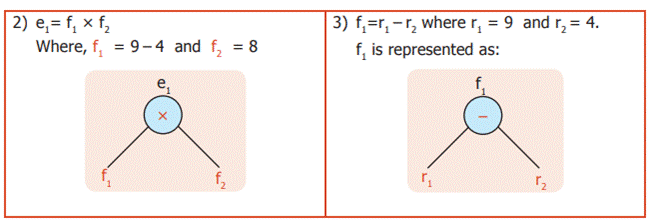
Similarly, the trees
can be developed from e2
4) Putting all together, we get the following tree diagram
●
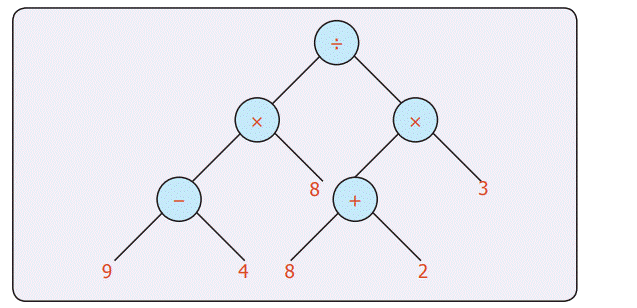
It is a picture which look like an
upside-down tree!
●
Every node has one or two branches. And
the leaves are numbers.
●
The branching nodes have operations on
them. It is called tree diagram and the tree diagrams are general ways of
representing arithmetical expressions.
●
Here trees are drawn upside down.
●
The root is at the top, the leaves are
at the bottom. Since all the arithmetical operations are binary (Involving two numbers)
we have only 2 way branching in the tree.
Example 1: In the flower
exhibition conducted at Ooty for 4 days the number of tickets sold on the first, second, third and fourth
days are 1,10,010; 75,070; 25,720 and 30,636
respectively. Find the total number of tickets sold.
Solution:
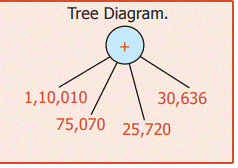
Number
of tickets sold on the first day = 1, 10, 010
Number
of tickets sold on the second day = 75, 070
Number
of tickets sold on the third day = 25, 720
Number
of tickets sold on the fourth day = 30, 636
Total
= 2, 41, 436
Total
number of tickets sold = 2, 41, 436.
Example 2:
In one year, a paper company had sold
6, 25, 610 notebooks out of a stock of 7, 50, 800 notebooks. Find the number of
notebooks left unsold.
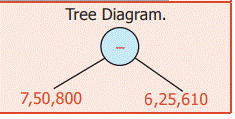
Solution:
Number
of Notebooks in stock = 7, 50, 800
Number
of Notebooks sold = 6, 25, 610
Number
of notebooks left unsold = 1, 25, 190
Example 3:
Vani and Kala along with three other
friends went to a butter milk shop. The cost of one butter milk is Rs, 6. If 9 more
friends joined them, then how much money did they have to pay? Vani said they
had to pay Rs.84 whereas Kala said they had to pay Rs.59. Who is correct?"
Solution:
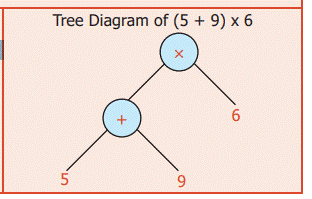
This
confusion can be resolved by using the brackets in the correct places like (5+9)
x 6. It is further clear from the tree diagram.
Therefore
Vani is correct
Example 4:
If a ration
shop has distributed 1, 00, 000 kg of rice to 5000 families, then find the
quantity of rice given to each family"
Solution:
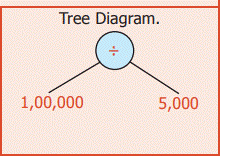
Quantity
of rice to be distributed to 5000 families =1, 00, 000 kg
Quantity
of rice distributed to each family =1, 00, 000÷5,000 =20 kg
Each
family was given 20 kg of rice.
Example 5:
Convert
into a Tree diagram (9 x 5) + (10 x 12)
Solution:
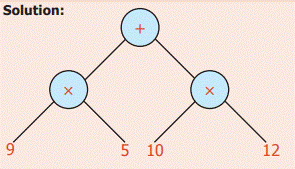
Example 6: Convert into a
Tree diagram (10 x 9) − (8 x 2) + 3
Solution:
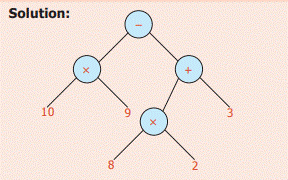
Example 7:
Convert
into a Tree diagram 
Solution:
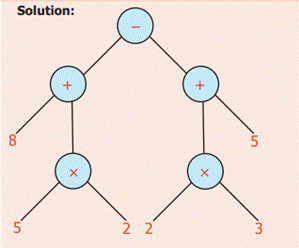
Example 8:
Convert
into a Tree diagram 
Solution:
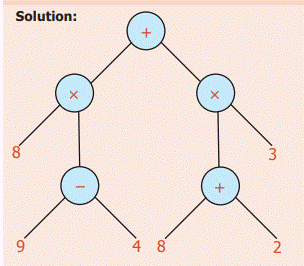
Example 9:
Convert
into a Tree diagram 
Solution:
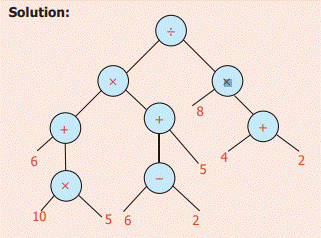
Example 10:
Convert into a Tree diagram 
Solution:
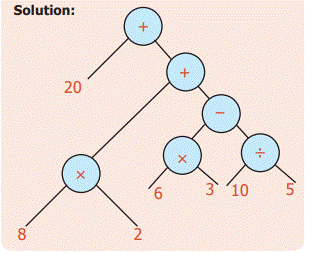
Example 11:
Convert
the tree diagram into numerical expression.
Solution:
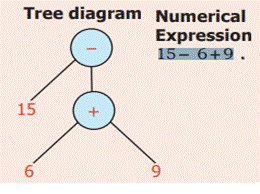
Example 12:
Convert
the tree diagram into numerical expression.
Solution:
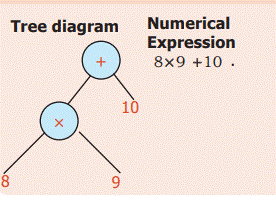
Example 13:
Convert
the tree diagram into numerical expression.
Solution:
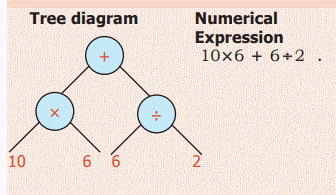
Example 14:
Convert
the tree diagram into numerical expression.
Solution:
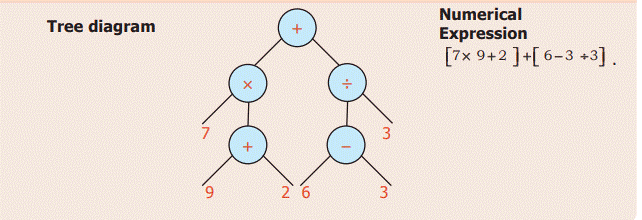
5.2 Conversion of Tree Diagrams Into Numerical Expressions
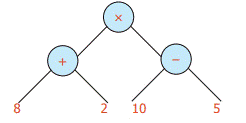
For instance, consider the tree
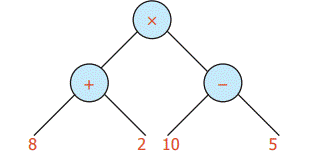
We could first find as
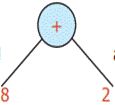10, then as
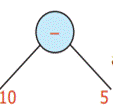5
When we multiply the results 10 and 5 we
get 50. Then the nodes for addition and subtraction are interchanged the value
remains the same which is represented using tree diagram as given below.
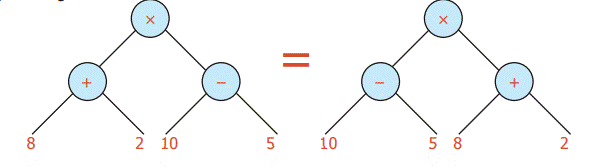
Does it mean that the branches also can be interchanged?
Yes, when the node is addition it is possible.
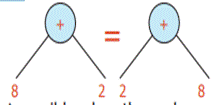
But it is not possible when the node represents subtraction.
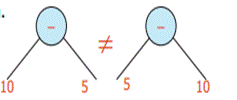
Therefore from this tree diagram.
The
expression can be converted into either (10−5) x (8 + 2) or (8+2) x (10−5)
or (2+8) x (10−5) or (10−5) x (2+8) without changing the value.
5.3 Conversion of Algebraic Expressions into
Tree Diagrams
There is more fun with trees. Observe the following trees
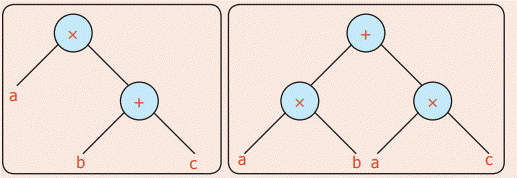
The above tree is nothing but the
familiar equation a× (b+c) = (a×b) + (a×c). Thus we can see the algebraic
expressions as trees.
• The tree on the left has less number
of nodes and looks simple.
• The tree on the right has more number
of nodes
• Can we conclude that the value of
both the trees are different.
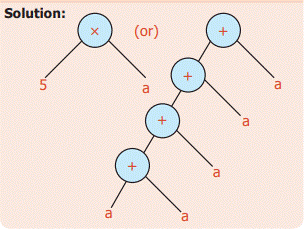
Example 15:
Convert
‘5a’ into Tree diagram
Solution:
Example 16:
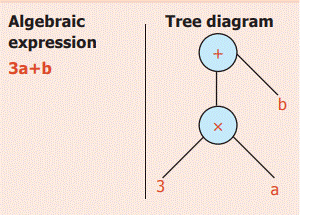
Convert
'3a+b' into Tree diagram
Solution:
Example 17:
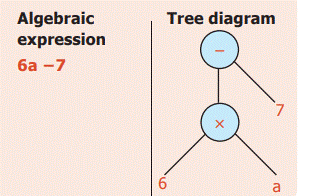
'6
times and 7 less’ Convert into a Tree diagram.
Solution:
Example 18:
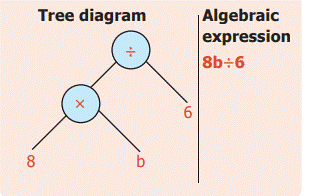
Convert
the tree diagram into an algebraic expression.
Solution:
Example 19:
Convert
the tree diagram into an algebraic expression.
Solution:
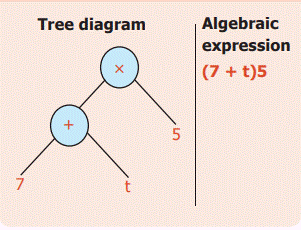
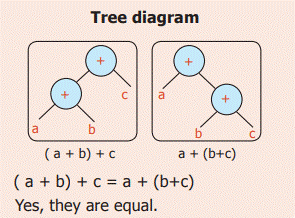
Example 20:
Verify whether given trees are equal or
not
Solution:
