Numbers

Basic Number Facts

· The numbers end with digits 1,3,5,7 and 9 are odd numbers.

E.g.: 5,9,15,99,1335 etc.

· The numbers end with digits 0,2,4,6 and 8 are even numbers.

E.g.: 6, 16, 82, 100 etc.

[Hence, they always come alternatively]

· Odd number + Odd number = Even Number.

E.g.: 5+17=22.

· Even number + Even number = Even Number.

E.g. 34+52=86.

· Odd number + Even number = Odd number.

E.g. 44+ 81=125.

· Odd number × Odd number = Odd number.

E.g.: 41 × 3= 123.

· Odd number × Even number = Even number.

E.g.: 41 × 8= 128.

· Even number × Even number = Even number.

E.g.: 40 × 4= 160.

· A factor is a number which divides the number exactly (gives remainder 0).

· Every factor of a number is less than equal to the number.

E.g.: 6 is a factor 24. 24/6=4 and 6 is less than the number.

1. Observe and complete

3+23=?

21+41=?

11+29=?

Solution:

3+23=26

21+41=62

11+29=40

From this, we observe that sum of odd numbers is always an odd number.

Prime Number and Composite Number

· The natural numbers having 2 factors 1 and the number itself are called prime numbers. E.g.: 2,3,7,17,29 etc.

o Total number of prime’s upto 100 is 25.

o Two prime numbers exactly having a difference of 2 are called twin primes. E.g.: (3, 5), (17, 19).

o If three successive prime numbers differ by 2, they are called prime triplet. Only prime triplet exist is 3, 5, 7.

· The natural numbers having more than 2 factors are called composite numbers. E.g.: 4, 9, 34, 45 etc.

o Composite numbers have atleast 3 factors.

· The number is a perfect number if the sum of the factors except the number gives the number. E.g.: 6 (6=1+2+3).

2. Express 68 and 128 as the sum of two consecutive primes. [HINT : Divide the number by 2 and add and subtract by same amount until you get a prime ]

Solution:

68 = 31+37

128 = 61+67

Rules of divisibility of numbers

· A number is divisible by 2 if its ones place contains 0,2,4,6, and 8. E.g.: 24, 36, 62 etc.

· Divisibility by 3

o A number is divisible by 3 if sum of digits is divisible by 3. E.g.: 39 -> 3+9=12 -> 1+2=3. 3 is divisible by 3.

o The sum of any 3 consecutive number is divisible by 3. E.g.: 11+12+13=36, 36 is divisible by 3.

· The number is divisible by 4 if last 2 digits are either 0 or divisible by 4. E.g.: 200,364,228 etc.

· The number is divisible by 5 if its ones place is either 0 or 5. E.g.: 5, 15, 100, 35 etc.

· The number is divisible by 6 if it is divisible both by 2 and 3.

· The number is divisible by 8 if the last 3 digits are either 0 or divisible by 8. E.g.:5000, 2344 etc.

· The number is divisible by 9 if the sum of the digits is divisible by 9. E.g.: 981 -> 9+8+1=18 -> 1+8=9

· The number is divisible by 10 if its ones place is 0. E.g.: 10, 30, 50, 80, 1030 etc.

· The number is divisible by 11 if the difference between the sum of the digits at odd and even places (from the right) of the number is 0 or divisible by 11.

3: Identify the numbers 2001, 2008, 2010, 2015, 2025 and 2032 that are divisible by 2 and 5 both.

Solution:

Indirectly it is asked to find the numbers divided by 10.

The number whose ones digit is 0 is divisible by 10. 2010 is the number.

Prime Factorisation

Expressing the number as a product of factors that are all prime numbers is called the prime factorisation of a number.

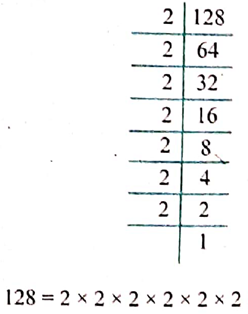
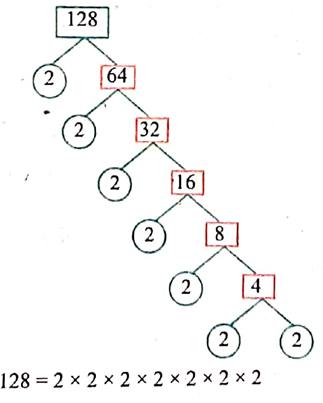
4. Find the prime factorisation of 128 in tree method and division method.

Solution:

Tree method

Division Method