FRACTIONS

1 Introduction

Fractions

Fractions is a part of a whole. The whole may be a single object or a group of objects.

For example, On Anbu’s birthday function, his father, mother and uncle have bought one cake each of equal size. At the time of cutting a cake, two friends were present for the celebration. He divided the cake into 2 equal pieces and gave the pieces to them. After some time, three of his friends arrived. He took another cake and divided it into 3 equal pieces and gave the pieces to them. Still he has one more cake at home. Anbu wanted to share it among his four family members. Third cake is divided into 4 equal pieces and given to them.

Following table shows how Anbu divided the cake equally according to the number of persons.

Here we have divided the whole into equal parts, each part is called a Fraction. We say a fraction as selected part(s) out of total number of equal parts of an object or a group. Each one’s share of dividing one cake between 2, 3 and 4 persons respectively.

Equivalent Fractions

Murali has one peanut bar. He wants to share it equally with Rani. So he divided it into two equal pieces, each one has got 1 piece out of 2, which is half of the peanut bar. They both decided to have half of their share in the morning break and another half in the evening break. Now the total number of pieces becomes 4. Each one has 2 pieces out of 4. That is 2 4 which is nothing but half of the peanut bar. Look at the figures. In both the type of sharing, they got only the same half of the peanut bar. Therefore

If the peanut bar had been divided into 6 equal pieces, each one would have got . What about each one’s share if it is divided into 8 equal pieces? We can observe that How do we get these equivalent fractions of ?

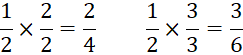
Hence, to get equivalent fractions of the given fraction, the numerator and denominator are to be multiplied by the same number.

Fractions are used in life situations such as

Ø To express time as quarter past 3, half past 4, quarter to 5.

Ø To say the quantum of work completed as quarter / half / three quarters of the work completed.

Ø To say the distance between two places as half a kilometre / two and half kilometre.

Ø To express the quantity of ingredients to be used in a recipe as half of the rice taken, half of the dhal taken etc.

2 Comparison of Unlike Fractions

Situation 1

Murugan has scored in Science and in Mathematics test. In which subject he has performed better? It is quite easy to say his performance is better in Mathematics. But can you find, the better performance of Murugan between the two test scores such as and in Mathematics. We need to convert both the marks as like fractions.

The equivalent fraction of is . Now we can compare the first test score with that of the second test score because both the scores are out of 20 marks. Here 18 > 13. So, > . Thus, Murugan has performed better in the first test.

Situation 2

In a Hockey tournament, Team A played 6 matches and won 5 matches out of it. Team B played 5 matches and won 4 matches out of it. If both the teams performed consistently in this way, find out which team will win the tournament?

From these we need to see which is greater or ? How can we find this? The total number of matches played by each team differs. By finding the equivalent fractions of and , we can equalize the number of matches played by team A and team B.

Note that the common denominator of equivalent fraction is 30, which is 5 ×6. It is the common multiple of both 5 and 6.

Here . So Team A will win the game.

Note

Ø To compare two or more unlike fractions, we have to convert them into 'like fractions'. These 'like fractions' are the equivalent fractions of the given fractions. The denominator of the 'like fractions' is the Least Common Multiple (LCM) of the denominators of the given unlike fractions.

Ø The process of finding the like fractions of the given unlike fractions can be made easier by finding the common multiples of the denominators of the unlike fractions.

Example 1 Vinotha , Mugilarasi, Senthamizh were participating in the water filling competition. Each one was given a bottle of equal volume to fill water in it within 30 seconds. If Vinotha filled portion of her bottle, Senthamizh filled portion of her bottle and Mugilarasi filled portion of her bottle, then who would get the first, second and third prize?

Solution

The equivalent fractions need to be written until the denominator becomes 4 which is the LCM of 2 and 4.

Equivalent fraction of

Here . Therefore, Senthamizh would get the first prize, Vinotha would get the second prize and Mugilarasi would get the third prize.

Example 2 Arrange , in ascending order.

Solution

Equivalent fractions of are

Equivalent fractions of are

Equivalent fractions of are

Therefore

The ascending order of given fractions is

3 Addition and Subtraction of Unlike Fractions

Situation

Venkat went to buy milk. He bought litre first and then he bought litre. He wanted to find how much milk he bought altogether? In order to find the total quantity of milk, he has to add and . That is . To add or subtract two unlike fractions, first we need to convert them into like fractions.

Example 3 Add and

Solution

These are unlike fractions, So first we need to convert them into like fractions.

The common multiple of 3 and 5 is 15.

Hence, we find the equivalent fractions of and with denominator 15.

In the above example, the common denominator is 15 (3×5). Now we observe that the numerator and denominator of the first fraction is multiplied by 5 which is the denominator of the second fraction. In the same way, the second fraction is multiplied by 3 which is the denominator of the first fraction. Now in finding the numerator of both the like fractions, we need to multiply the numerator of the first fraction by 5 and the numerator of the second by 3. In the denominator, 3×5 and 5×3 are of course the same. Thus, the technique of finding the like fraction is called Cross Multiplication technique.

That is

Example 4 Simplify :

Solution

By Cross Multiplication technique,

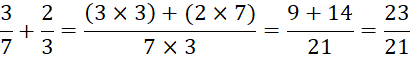
Example 5 Simplify :

Solution

Common multiple of 2 and 4 is 4

Equivalent fraction of is

Now,

Example 6 Find the difference between and

Solution

By Cross Multiplication technique,

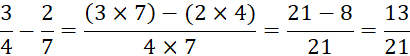
4 Improper and Mixed Fractions

Situation

Iniyan had 5 idlis for his breakfast. When he was about to eat, his friend Abdul came. He wanted to share it equally with his friend Abdul. Both of them have taken 2 each and of the remaining idli.

Each one has eaten 2 full idlis and idli. This can be represented as . This representation is called a mixed fraction. Thus, a mixed fraction is the sum of a whole number and a proper fraction. Also we can express an improper fraction as a mixed fraction by dividing the numerator by denominator to get quotient and remainder. Thus, any mixed fraction can be written as

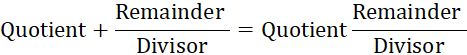
Another way to share these idlis is as follows: Now can you see how many halves are there in 5 idlis. There are 10 halves. If we share these idlis each time, then Iniyan and Abdul has eaten 5 halves each. That is which is same as .

Thus, any improper fraction can be written as mixed fraction as

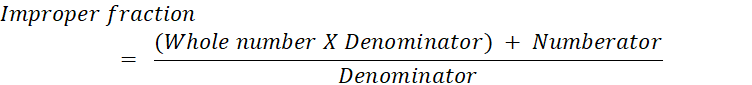
Example 7 Convert into an improper fraction.

Solution

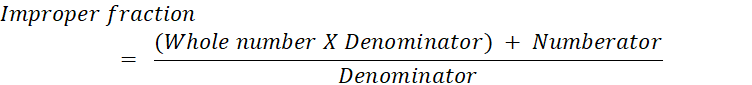
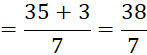
Example 8 Convert into a mixed fraction.

Solution

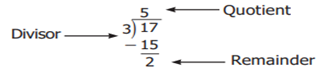
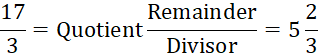
5 Addition and Subtraction of Mixed Fractions

Example 9 Saravanan’s father bought of cloth. Find the total length of the cloth bought by him?

Solution

Total length of the cloth =

First we add whole numbers: 2 + 2 + 1 = 5 m

Then, add the fractions:

Therefore, the total length of the cloth bought =

Example 10 Add:

Solution

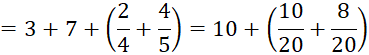
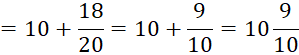
Example 11 Simplify:

Solution

Here 9 > 3 and So we proceed as follows: We convert the mixed fraction into improper fraction and then subtract.

and

Common multiple of 4 and 6 is 12.

Now,

6 Multiplication of Fractions

Situation 1 (Multiplication of a fraction by a whole number)

Sunitha wanted to give kg of sweets to each of her 3 friends. So she went to a sweet stall and she asked the salesman to give three kg packets of sweets, how much sweet did she buy?

Solution

Weight of three kg packets of sweets kg

Situation 2 (Multiplication of a fraction using the operator ‘of’)

Kannan has 30 beads and Kanmani has one sixth of it. How many beads does Kanmani have?

Solution

The number of beads that Kanmani has = of 30 beads

beads

Situation 3 (Multiplication of a fraction by another fraction)

Sunitha bought three kg sweet packets for her three friends from a sweet stall. But 6 of her friends had come to her home. So she decided to divide each kg sweet packets into halves. If she has done in that way, what would be the weight of the sweet packet that each one of her friend will receive?

Solution

The weight of the sweet packets that each one of her friends will receive = half of kg

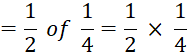
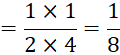
Example 12 Maruthu, a milk man has 4 bottles of milk each containing litres. How much milk does he have in all?

Solution

Since Maruthu has 4 bottles of milk and each containing litres, he has 4 times of litres of milk.

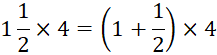
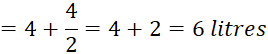
7 Division of Fractions

Situation 1

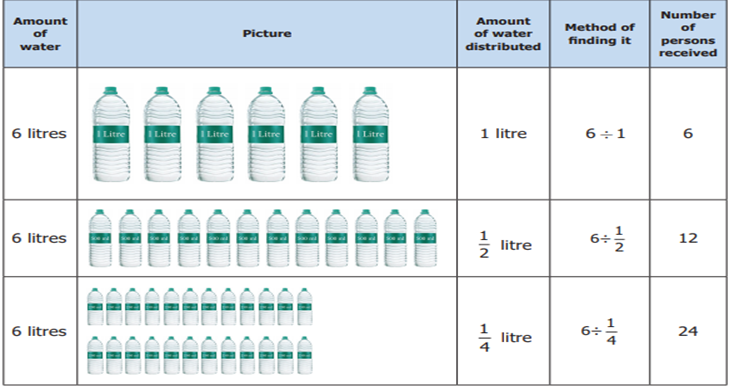
A camp was organized in a school in which12 students participated. The camp leader wanted to divide them into groups of 2 students. How many groups were there?

There were 6 groups which was got by the division of 12 by 2. That is 12 ÷ 2 = 6 which means there are six 2’s in 12.

If the camp leader distributes 6 litres of water in litre water bottles to the students, then how many students will get water bottles? This means fi nding how many litres are there in 6 litres. For this we need to calculate .

Solution Let us describe the situation

Example 13 Divide

Solution

Example 14 A rod of length 6m is cut into small rods of length m each. How many small rods can be cut?

Solution

The number of small rods =