INTEGERS

1 Introduction

We already have learnt about natural numbers, whole numbers and their properties which were dealt in the first term. Now we shall know about another set of numbers.

Situation

The teacher sees that Yuvan and Subha are ready to play a game with a deck of playing cards. Two different coloured tokens (blue and yellow here) are taken so that they represent the position on a number strip which is numbered from 0 to 20 with 0 as the starting point and which can be extended further.

Consider the cards A, J, Q, K and cards from 2 to 10. Here, let A, J, Q and K denote the numbers 1,11,12 and 13 respectively. We have two designs ♠ ♣ in black colour and two designs ♥ ♦ in red colour inside a deck of cards. Let the joker card represent 0.

Rules for the game

i) If a black card is picked, the player should move the token forward and if a red card is picked, the player should move the token backward as per the number shown on the card.

ii) Whoever reaches the number 20 first will be declared as the winner.

(more students can play this game by choosing different coloured tokens).

Observe the following conversation

Yuvan : Subha, I have chosen the blue token.

Subha : Okay, Then I shall take the yellow token.

Yuvan : The number strip is ready as shown below and let both the tokens be placed at the starting position 0. Shall we start playing?

Subha : Yes. I shall pick a card first. I have picked a black card and it shows 5. So I will move forward to keep my yellow token at 5 on the number strip.

Yuvan : Now, I pick …It is black card again and it shows A on it. I will keep my blue token by moving one step forward at 1 on the number strip.

Subha : I pick a red card now and it shows 2 on it. I need to move backward by 2 steps and I shall keep my token at 3. Is it correct, Yuvan?

Yuvan : Fine Subha . Now, I too have picked the red card and it shows A again. Oh, no..! I will move backward by one step to be again at the starting position 0.

Subha : I am 3 steps ahead of you! Now, I have the red card showing 4 on it. I need to move 4 places backward from 3. But, where shall I keep my token, Yuvan? I moved 3 places only but need one more place behind 0. There is no number on the left of 0.

Subha : Shall I mark it as 1 again?

Yuvan : No, Subha. That won’t be correct. We know that 1 already exists to the right of 0.

Subha : Then, what should I do? I can’t move to the left of '0'. Is the game over or shall I pick another card to continue?

The Teacher intervenes …

Teacher : Yuvan and Subha, why can't you think of extending the number strip to the left of 0 as *1, *2 ,*3 and so on such that the distance between *1 and 0 is the same as the distance between 0 and 1 and also the distance between *2 and 0 is the same as the distance between 0 and 2 and extending likewise?

Subha : Yes Teacher, I understand that the * will now indicate that the numbers are on the left of 0, and also the numbers are less than 0.

Teacher : To sustain the interest in the game, continue playing with a small addition in the rule as whoever reaches *20 first, will also be considered as the winner!

Yuvan : So Subha, you shall keep it at *1.

Yuvan : What, if you pick the red card again which shows 4 ?

Subha : I am clear Yuvan. I will move backward 4 places from *1 to keep my token at *5.

Yuvan : Well said…! What can you say, assuming that I am at 5?

Subha : Yes, Yuvan. We will be at the same distance but on the opposite sides of '0'. Am I right?

Yuvan : Yes. you are right but your value is less than mine as you go to the left of '0'.

From the above game, we understand that there is a need to go beyond 0 on to its left! We also observe that as 1 is to the right of 0, there should exist *1 to its left with the same distance as 1 and it extends on both sides in the same way.

We generalise this * symbol to ‘–’ (minus or negative sign) to denote the numbers less than '0' which conveys the meaning as less, deficit, reduce, down, left, etc.,

2 Introduction of Integers and its representation on a number line

We know that when zero is included to the set of natural numbers then the set of numbers is called as Whole numbers.

Now, let us recall the number line which shows the representation of whole numbers.

We have seen the need to extend the number line beyond 0 to its left. We call the numbers –1, –2, –3, … (to the left of zero) as negative numbers or negative integers and the numbers 1, 2, 3,… ( to the right of zero) as positive numbers or positive integers. Hence, the new set of numbers …, -3, -2, -1, 0, 1, 2, 3, … are called Integers. It is denoted by the letter ‘Z’. The Integers are shown in the number line below.

The 'plus' and 'minus' sign before a number tells, on which side the number is placed from zero. ‘–’ symbol in front of a number is read as 'negative' or 'minus'. For example, –5 is read as negative 5 or minus 5.

Note

Ø The number line can be shown both in horizontal and vertical directions.

Ø The number 0 is neither positive nor negative and hence has no sign.

Ø Natural numbers are also called as positive integers and Whole numbers are also called as non-negative integers.

Ø The positive and the negative numbers together are called as Signed numbers. They are also called as Directed numbers.

Ø A number without a sign is considered as a positive number. For example, 5 is considered as +5.

Example 1 Draw a number line and mark the integers 6, –5, –1, 4 and –7 on it.

Solution

2.2 Opposite of a number

The idea of opposite of a number is not a new one. A few situations like, a man makes a profit of ₹ 500 or he loses ₹ 500 by selling an article; credit and debit of ₹ 75000 in a cash transaction of a business are ‘opposite’ to each other.

Situation

Suppose two rabbits R and S jump along a number line (like) on the opposite sides of 0. Rabbit R jumps 2 steps 3 times to the right of 0 and Rabbit S jumps 3 steps 2 times to the left of 0 as shown in the figure below. Where will both of them stand on the number line? Are they at equal distance from 0?

Clearly, the rabbit R stands at 6 and the rabbit S stands at −6 on the number line. The distance from 0 to 6 on the number line is 6 units and the distance from 0 to −6 on the number line is also 6 units .The numbers 6 and −6 are at the same distance from 0 on the number line. That is, the rabbits R and S stand at the same distance from 0, but in opposite directions.

Here, 6 and −6 are opposite to each other. That is, two numbers that are at the same distance from 0 on the number line, but are on the opposite sides of it, are opposite to each other. For every positive integer, there is a corresponding negative integer and vice versa. The opposite of each integer is shown in the figure.

Now, it is easy to write the opposite of the numbers −7, 12, −225 and 6000. Note that, the opposite of a positive integer is negative, and the opposite of a negative integer is positive, whereas the opposite of zero is zero.

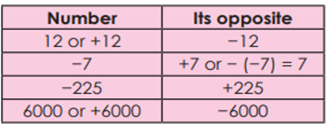
The “opposites” are naturally more convenient to relate and understand with many of our daily-life situations like saving-spending, credit-debit, height above-below, where

i) the saving is treated as positive and the spending is treated as negative.

ii) a credit is considered positive whereas a debit is considered negative.

iii) the height above the sea level is regarded as positive and the height below the sea level is regarded as negative.

Example 2 Represent the following situations as integers:

i) A gain of ₹1000 ii) 20°C below 0°C iii) 1990 BC (BCE)

iv) A deposit of ₹15847 v) 10 kg below normal weight

Solution

i. As gain is positive, ₹1000 is denoted as + `1000.

ii. 20°C below 0°C is denoted as −20°C.

iii. A year in BC (BCE) can be considered as a negative number and a year in AD (CE) can be considered as a positive number. Hence, 1990 BC (BCE) can be represented as −1990.

iv. A deposit of ₹15847 is denoted as + ₹15847.

v. 10 kg below normal weight is denoted as −10 kg.

Example 3 Using the number line, write the integer which is 5 more than −6.

Solution

From −6, we can move 5 units to its right to reach −1 as shown in the figure.

3 Ordering of Integers

We have already seen the ordering of numbers in the set of natural and whole numbers. The ordering is possible for integers also.

2.3.1 Predecessor and Successor of an Integer

Recall that for a given number its predecessor is one less than it and its successor is one more than it. This applies for integers also.

Example 4 Find the predecessor and successor of i) 0 and ii) −8 on a number line.

Solution

Place the given numbers on the number line then move one unit to their right and left to get the successor and the predecessor respectively.

We can see that the successor of 0 is +1 and the predecessor of 0 is −1 and the successor of −8 is −7 and the predecessor of −8 is −9.

3.2 Comparing Integers

Ordering of integers is to compare them. It is very easy to compare and order integers by using a number line.

When we move towards the right of a number on the number line, the numbers become larger. On the other hand, when we move towards the left of a number on the number line, the numbers become smaller.

We know that 4 < 6 , 8 > 5 and so on. Now let us consider two integers say −4 and 2. Mark them on the number line as shown below.

Fix −4 now. See whether 2 is to the right or the left of −4. In this case, 2 is to the right of−4 and in the positive direction. So, 2 > −4 or otherwise −4 < 2.

Example 5 Compare −14 and −11

Solution

Draw number line and plot the numbers −14 and −11 as follows.

Fixing −11, we find −14 is to the left of −11. So, −14 is smaller than −11. That is, −14 < −11.

Example 6 Arrange the following integers in ascending order: −15, 0, −7, 12, 3, −5, 1, −20, 25, 18

Solution

Step 1: First, separate the positive integers as 12, 3, 1, 25, 18 and the negative integers as −15, −7, −5, −20

Step 2: We can easily arrange positive integers in ascending order as 1, 3, 12, 18, 25 and negative integers in ascending order as −20, −15, −7, −5.

Step 3: As 0 is neither positive nor negative, it stays at the middle and now the arrangement −20, −15, −7, −5, 0, 1, 3, 12, 18 and 25 is in ascending order.