PERIMETER
AND AREA
1 Introduction
We come across many
situations in our day to day life which deal with shapes, their boundaries and
surfaces. For example,
Ø A
fence built around a land.
Ø Frame
of a photograph.
Ø Calculating
the surface of the wall to know the quantity of the paint required.
Ø Wrapping
the textbooks and notebooks with brown sheets.
Ø Calculating
the number of tiles to be laid on the floor.
Some situations need to
be handled tactfully and efficiently for the following reasons.
Ø Using
the optimum space to build a dining hall, kitchen, bedroom etc., in
constructing a house in the available land and planning of materials required.
Ø Arranging
the things like cot, television, cup-board, table etc., in the proper place within
the available space at home.
Ø Reducing
the expenses in all the above activities.
In this context,
learning of perimeter and area will be of great importance.
2 Perimeter
The length of the
boundary of any closed shape is called its perimeter.
Hence, ‘the measure around’ of a closed shape is called its perimeter. The unit of perimeter is the
unit of length itself. The units of length may be expressed in terms of metre,
millimetre, centimetre, kilometre, inch, feet, yard etc.,
2.1 Perimeter of a Rectangle
Perimeter of a rectangle
= Total boundary of the rectangle
= length + breadth +
length + breadth = 2 length + 2 breadth = 2 (length + breadth)
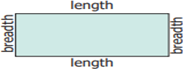
Let us denote the
length, breadth and the perimeter of a rectangle as l, b and P respectively.
Perimeter of the
rectangle, P= 2 x (l + b) units
Example
1 If the length of a rectangle is 12 cm and the
breadth is 10 cm, then find its perimeter.
Solution
l = 12 cm b = 10 cm
P = 2 (l + b) units = 2
(12 + 10) = 2 × 22 = 44 cm
Perimeter of the rectangle
is 44 cm.
2.2 Perimeter of a Square
Perimeter of a square =
Total boundary of the square
= side
+ side + side + side = (4 × side) units
If the side of a square is ‘s’ units, then
Perimeter of the square,
P = (4 × s) units = 4s units
Example
2 The side of a square is 5 cm. Find its
perimeter.
Solution
s = 5 cm
P = (4 × s) units
= 4 × 5 = 20 cm
Perimeter of the square
is 20 cm.
2.3 Perimeter of a Triangle
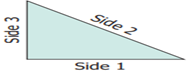
Perimeter of a triangle
= Total boundary of the triangle
= side
1 + side 2 + side 3
If three sides of a
triangle are taken as a, b and c, then
the
Perimeter of the triangle, P = (a + b + c) units.
Example
3 Find the perimeter of a triangle whose sides
are 3 cm, 4 cm and 5 cm.
Solution
a = 3 cm b = 4 cm c = 5
cm
P = (a + b + c) units
= 3 + 4 + 5 = 12 cm
Perimeter of the
triangle is 12 cm.
Example
4 Find the length of the rectangular black board
whose perimeter is 6 m and the breadth is 1 m.
Solution
Perimeter of the black board, P= 6 m
Breadth of the black
board, b=1 m
length,
l =?
2 (l + b) = 6 
2
(l + 1) = 6
l + 1 = 
= 3 l
= 3 – 1 = 2 m
The
length of the black board is 2 m.
Example
5 Find the side of the equilateral triangle of
perimeter 129 cm.
Solution
Perimeter of the
equilateral triangle, P = 129 cm
a
+ a + a = 129
3
x a = 129
a
= 43 cm
The side of the
equilateral triangle is 43 cm.
Example
6 Find the cost of fencing a square plot of side
12 m at the rate of Rs.15 per metre.
Solution
Side of a square plot =
12 m
Perimeter of the square plot
= (4 × s) units
= 4 ×
12 = 48 m
Cost of fencing the plot
at the rate of Rs.15 per metre = 48 × 15 = Rs.720
3 Area
The space of the tray is
called the Area of the tray. Thus, the area of any closed shape is the surface
occupied by the number of unit squares within its boundary.
Suppose each side of a
biscuit is of 1 inch length, then the area of the tray is 12 square inches.
3.1 Area of a Rectangle
The area of any
rectangle = (length x breadth) square units.
= (l x
b) sq. units.
Example
7 Find the area of a rectangle of length 12 cm
and breadth 7 cm.
Solution
Length of the rectangle,
l = 12 cm.
Breadth of the
rectangle, b = 7 cm.
Area of the rectangle A
= (l x b) sq. units.
= 12 x
7 = 84 sq. cm.
3.2 Area of a Square
If the length and breadth
of a rectangle are equal, then it becomes a square.
Area of the rectangle =
(length x breadth) square units.
= (side
x side) sq. units.
= (s x s) sq. units.
= Area of a square
Therefore area of a
square = (s x s) sq. units.
Example
8 Find the area of a square of side 15 cm.
Solution
Side of the square, s =
15 cm
Area of the square, A = (s x s) sq. units.
= 15 x
15
= 225
sq. cm. (or) 225 cm2
3.3 Area of a Right Angled Triangle
In a right angled
triangle one of the sides containing the right angle is treated as its base (b
units) and the other side as its height (h units).
When a rectangular sheet
is cut along its diagonal, two right angled triangles are obtained.
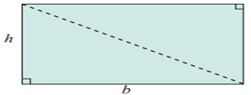
Area of two right angled
triangles = Area of the rectangle
2 x Area of a right
angled triangle = l x b
Area of the right angled
triangle = 
sq. units.
The length and breadth
of the rectangle are respectively the base (b) and height (h) of the right
angled triangle.
Hence, area of the right
angled triangle = 
(b x h) sq.units.
Example
9 Find the area of a right angled triangle whose
base is 18 cm and height is 12 cm.
Solution
Base, b = 18 cm Height,
h = 12 cm
Area, A = (b x h) sq. units
= (18 x 12)
= 108
sq. cm. (or) 108 cm2
4 Perimeter and Area of Combined Shapes
A Combined shape is the
combination of several closed shapes. The perimeter is calculated by adding all
the outer sides (boundaries) of the combined shape. The area is calculated by
adding all the areas of closed shapes from which the combined shape is formed.
Example
10 Find the perimeter of the given figure.
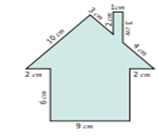
Solution
Perimeter = Total length
of the boundary
= (6 + 2 + 10 + 3 + 2 + 1 + 3 + 4 + 2 + 6 +
9) cm
= 48 cm.
Example
11 Find the perimeter and the area of the
following ‘L’ shaped figure.
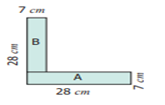
Solution
Perimeter = (28 + 7 + 21
+ 21 + 7 + 28) cm.
= 112 cm.
To
find the area of the L shaped figure, it is divided into two rectangles A and
B.
Rectangle-A Rectangle-B
l = 28
cm l = 21 cm
b = 7
cm b = 7 cm
A = l x
b sq. cm A = l x b sq.
cm.
= 28 x 7 = 21 x 7
= 196 sq. cm = 147 sq.
cm
The
area of the ‘L’ shaped figure = (196 + 147) sq. cm = 343 sq. cm.
4.1 Impact on Removing / Adding a portion from / to a given
shape
Consider a rectangle of
sides 8 cm and 12 cm.
Length, l = 12 cm;
Breadth b = 8 cm.
Area, A = (l x b) sq.
units.
= 12 x
8 = 96 sq. cm.
Perimeter, P = 2 (l + b)
units.
= 2 (12
+ 8) = 40 cm
Find the area and
perimeter of the rectangle in the following situations and observe the changes.
Situation
1
A square of side 3 cm is
cut at a corner of the rectangle.
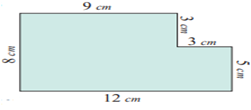
Area, A = (l x b) – (s x
s) sq. units.
= (12 x
8) – (3 x 3) = 87 sq. cm.
Perimeter, P = (Total
boundary) units.
= 8+12+5+3+3+9 = 40 cm.
The perimeter is not
changed. But the area is reduced.
Example
12 Four identical square floor mats of side 15 cm
are joined together to form either a rectangular mat or a square mat. Which mat
will have a larger area and a longer perimeter?
Solution
Perimeter of a
rectangle, P = 2 (l + b) units.
= 2 (60+15) cm. = 150 cm.
Area of a rectangle, A =
(l x b) sq. units.
= 60 x 15 = 900 sq. cm.
Perimeter of a square, P
= (4 × s) units
= (4 x 30) cm = 120 cm
Area of a square, A = (s
x s) sq. units.
= 30 x 30 = 900 sq. cm.
There is no change in
their areas. But, the rectangular mat will have longer perimeter
5 Area of Irregular Shapes
The area of the shapes
like triangle, square etc., are found by standard formulae. But we can find the
approximate area of shapes like leaves as follows.
Place a leaf on a graph
sheet and trace its boundary.
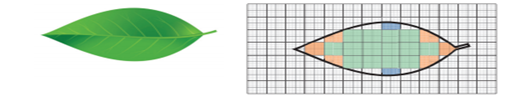
Now observe the squares
of size 1 cm x 1 cm inside of this boundary. We get complete squares (Green),
partial but bigger than half squares (Orange) and half squares (Blue). The
smaller than half squares which have negligible area are omitted.
Now the approximate area of the leaf = (Number of full
squares + Number of more than half squares
+ 
x Number of half squares)
sq. units
= (14 +
6 + x 2) sq. cm
= 21 sq. cm
6 Expressing the Area in Square Units
Consider a square of
side 1 cm. Therefore, its area is 1 sq. cm (1 cm2
). Divide one of its sides into 10 equal parts. One such part is equal
to 1 mm. We know that 1 cm = 10 mm. That is a square of side 1 cm is made up of
100 small squares with 1 mm square area each.
Therefore, the side of
this square is 10 mm and the area of this square = side x side =10 mm x 10 mm =
100 sq. mm (100 mm2 ).
Therefore, the area of a
square with 1 cm side is 1 cm2 = 100 mm2
.
Similarly, the other
conversions can also be done. For example,
i)
1 cm2 = 10 mm x 10
mm
= 100 mm2
ii)
1 m2 = 100 cm x 100
cm
= 10,000 cm2
iii)
1 km2 = 1000 m x
1000 m
= 10,00,000 m2