SYMMETRY

1 Introduction

Looking at our surroundings, we see that most of the objects appear with certain beauty. Do you know why these objects look beautiful? The balanced harmony at a perfect ratio makes these objects look beautiful. This kind of organized pattern is called symmetry. Symmetry plays a vital role in many fields of work like making toys, drawings, kolams, household goods, manufacturing vehicles, construction of buildings etc.,

2 Line of Symmetry

In the given figures, the red coloured line divides each figure into two equal halves and suppose we fold them along that line, we will see that one half of each figure exactly coincides with the other half. Such figures are symmetrical about that line and that line is called the line of symmetry or the axis of symmetry.

A figure may have one, two, three or more lines of symmetry or no line of symmetry.

Symmetry can be found anywhere in nature as well as in man-made objects. A few of them are leaves, insects, flowers, animals, note books, bottles, architecture, designs and shapes, etc.,

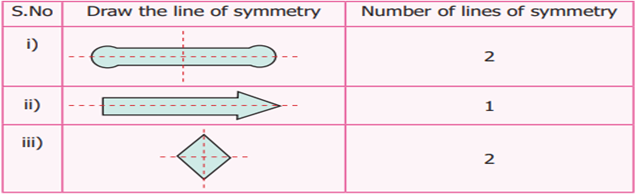
Example 1 Draw the lines of symmetry for the given figures and also find the number of lines of symmetry

Solution:

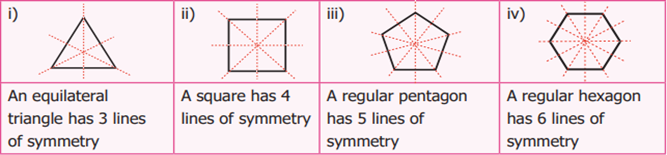
Example 2 Draw the lines of symmetry for an equilateral triangle, a square, a regular pentagon and a regular hexagon and also find the number of lines of symmetry.

Solution

3 Reflection Symmetry

Standing in front of a mirror, Kumaran was getting ready to celebrate his birthday. He noticed a beautiful sentence I LOVE MOM written on his T-shirt which was presented by his uncle.

In these words, he saw I and MOM were looking the same in the mirror. But the word LOVE did not appear the same. It looked as .

Out of curiosity, he took out some alphabet cards and started checking which of the alphabets would look the same in the mirror. He found a few alphabets A, H and I look the same in the mirror, because they have lines of symmetry.

Already we know that a line of symmetry divides the figure into two equal halves. When you keep a mirror along the line of symmetry the other half of the figure gets reflected by the mirror and it looks the same. This is known as reflection symmetry or mirror symmetry.

A shape has reflection symmetry if it has a line of symmetry.

When an object is seen in a mirror, the image obtained on the other side of the mirror is called its reflection.We observe that an object and its mirror image are symmetrical with reference to the mirror line. If the paper is folded, the mirror line becomes the line of symmetry.

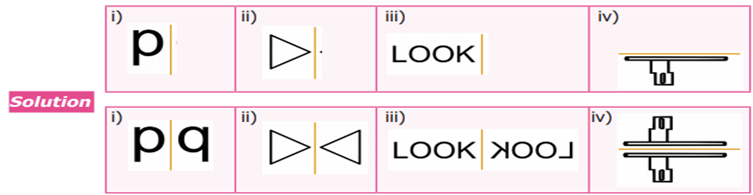
Example 3 Draw the reflection image of the following figures about the given line

Example 4 Assuming one shape is the reflection of the other, draw the mirror line for each of the given figures.

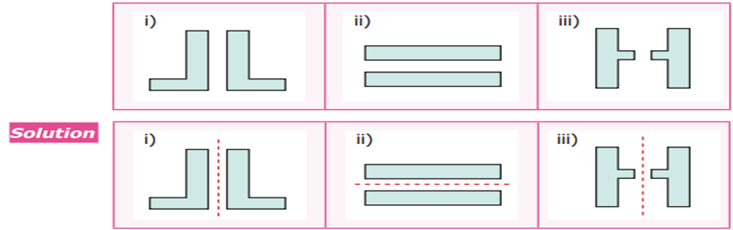
Example 5 What words will you see if a mirror is placed below the words MOM, COM, HIDE and WICK?

4 Rotational Symmetry

We have already learnt about rotation. Rotation means turning around a centre. The paper windmill, merry-go-round, fan, tops, wheels of vehicles, fidget spinner are few examples of rotating objects that we see in our life.

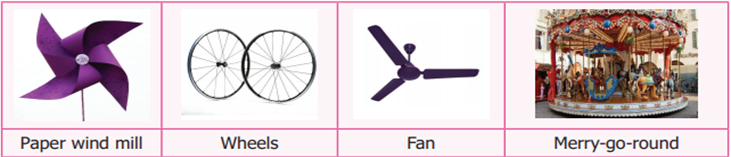
When one rotation is completed, the rotating object comes back to the position where it started. During a complete rotation, the object moves through 360°.

Situation

1) Take two rectangular biscuits from the same packet and put one on the other. Holding one biscuit firmly rotate the other on it about the centre.

How many times does it fi t exactly on the other in a complete rotation? Two times.

2) In the example given below, if you rotate the fidget spinner about the centre, there are three positions in which the fidget spinner matches exactly the same in a full rotation.

3) Place a set square (containing angles 60°, 30° and 90°) on a paper and draw an outer line around it. Type of triangle you get- Scalene triangle. If you rotate it about the centre, there is only one position in which the set square fits exactly inside the outer line.

In the above situations 1 and 2, the total number of times the rectangular biscuit and the fidget spinner matches exactly with itself in one complete rotation is 2 and 3. This is called the order of rotational symmetry. In situation 3, the set square matches itself only once in one complete rotation and hence has no rotational symmetry.

An object is said to have a rotational symmetry if it looks the same after being rotated about its centre through an angle less than 360° (If the order of rotation of an object is atleast two).

Example 6 A man-hole cover of a water sump is in square shape.

i) In how many ways we can fix that to close the sump?

ii) What is its order of rotational symmetry?

Solution

i) We can fix it in 4 ways as shown above.

ii) The order of rotational symmetry is 4.

Example 7 Find the order of rotation for the following shapes.

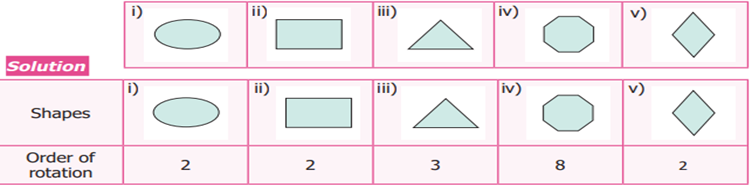
5 Translational Symmetry

Look at the following figures:

Here a particular pattern or design is continued throughout. The pattern changes its place without rotation or reflection. The exact image is found without changing its orientation.

Thus, translation symmetry occurs when a pattern slides to a new position. The sliding movement involves neither rotation nor reflection.

Example 8 Which pattern is translated in the given kolams?

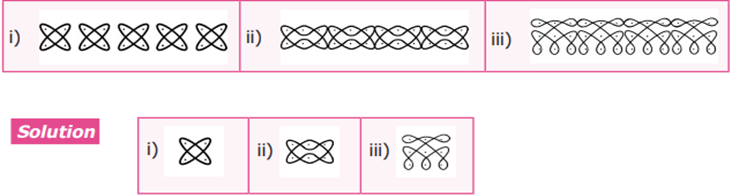
Example 9 Translate the given pattern and complete the design in the rectangular strip

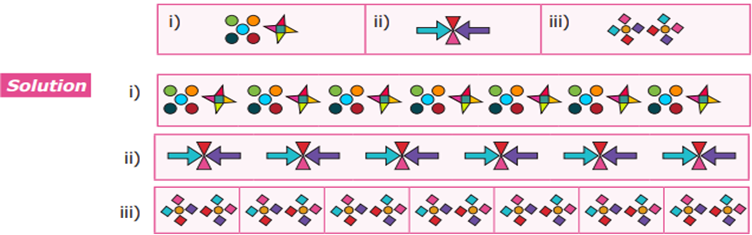
Summary

Ø The line that divides any figure into two equal halves such that each half exactly coincides with the other is known as the line of symmetry or axis of symmetry.

Ø A shape has reflection symmetry if it has a line of symmetry.

Ø An object is said to have a rotational symmetry if it looks the same after being rotated about its centre through an angle less than 360°.

Ø The total number of times a figure coincides with itself in one complete rotation is called the order of rotational symmetry.

Ø Translation symmetry occurs when an object slides to a new position. The sliding movement involves neither rotation nor reflection.