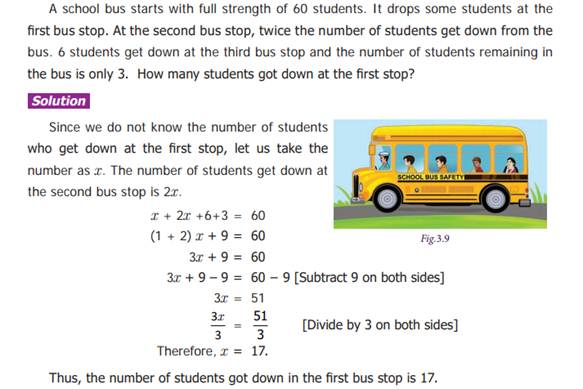Algebra

Terms and Co-efficient:-

Algebraic expressions are formed by combining variables and constants using the mathematical operations addition and subtraction.

Terms: -

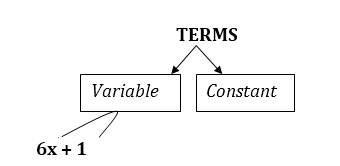
The expression 6x + 1 is obtained by adding two parts 6x and 1and 6x and 1 are known as terms. The term 6x is a variable and the term 1 is a constant, since it is not multiplied by a variable. So, 6, x are the factors of the term 6x.

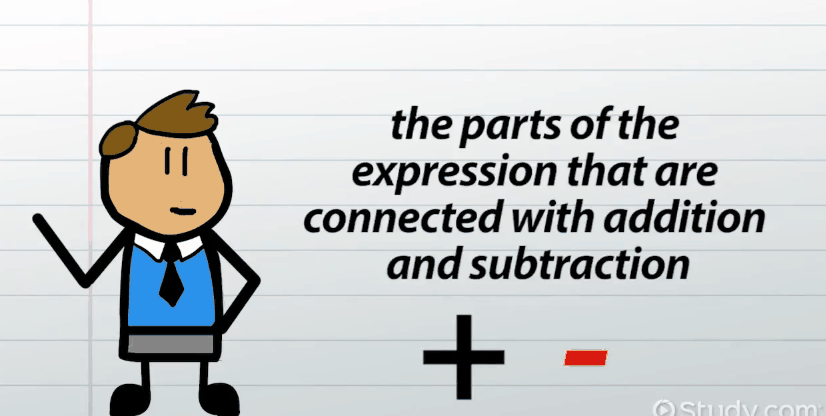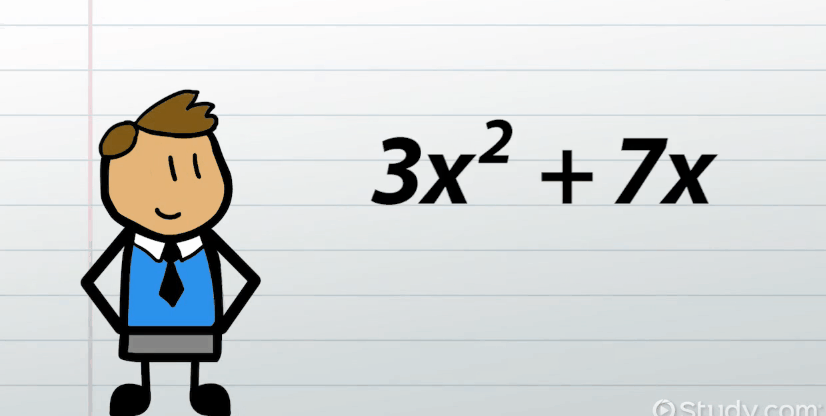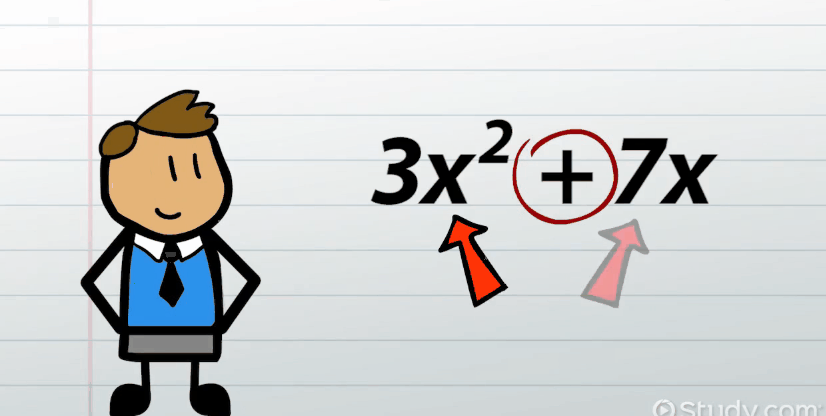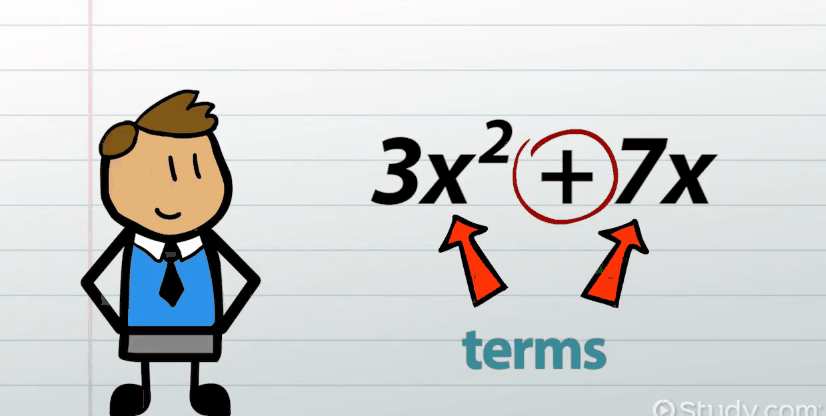
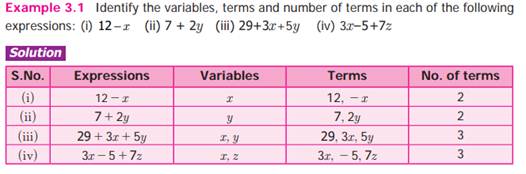
· An expression may have one, two, three or more terms.

· A term may be any one of the following:

a) A constant such as 8, −11, 7, −1 and so on.

b) A variable such as x, a, p, y and so on.

c) A product of two or more variables such as xy, pq, abc, and so on.

d) A product of constant and a variable/variables such as 5x, −7pq, 3abc and so on.

· An expression with one term is called a monomial.

For example, the expression 2x is a monomial.

· An expression with two terms is called a binomial.

For example, the expression 2x + 3y is a binomial

· An expression with three terms is called a trinomial.

For example, the expression 2x + 3y + 4z is a trinomial

· An expression with one or more terms is called a polynomial.

All the expressions given above are polynomials.

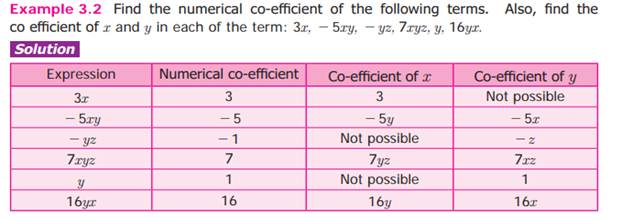
Co-efficient of a term:-

A term of an algebraic expression is a product of factors and each factor or product of factors is called the co-efficient.

In the term 5xy,

The co-efficient of ‘xy’ is 5.

The co-efficient of ‘5y’ is x.

The co-efficient of ‘y’ is 5x.

He constant 5 is called the numerical co-efficient, and others are called simply co-efficient. If no numerical co-efficient appears in a term, then the co-efficient is understood to be 1.

Like and unlike terms:-

For example, the expression 7x + 5x + 12x – 16 has 4 terms

· The terms of an expression having the same variable are called like terms.

For example: - The first three terms have the same variable factor x. We say that 7x, 5x and 12x are like terms.

· The terms of an expression having different variable(s) are called unlike terms.

For example: - the terms 12x and −16 have different variable factors. The term 12x has the variable x and the term −16 is a constant. Such terms are called unlike terms.

Value of an algebraic expression:-

Follow the steps to obtain the value:-

Step −1: Study the problem. Fix the variable and write the algebraic expression.

Step −2: Replace each variable by the given numerical value to obtain an arithmetical expression.

Step −3: Simplify the arithmetical expression by BIDMAS method.

Step −4: The value so obtained is the required value of the expression.

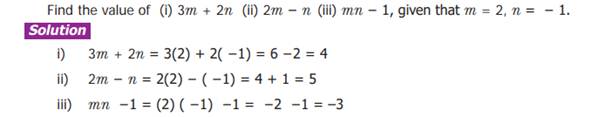
Addition and Subtraction of Algebraic expressions:-

To add the algebraic expressions 11y + 7 and 5y − 3, where 11y and 5y are like terms with a variable y and 7 and −3 are constants (like terms).

Hence,

(11y + 7) + (5y − 3) = [11y + 5y] + [7 + (− 3)]

= [(11 + 5) y] + (7 − 3)]

= 16y + 4.

Subtraction of a term can be looked as addition of its additive inverse.

For example, to subtract 6y from 12y, we can add 12y and (− 6y).

Hence,

12y + (− 6y) = 12y − 6y

= (12 − 6) y

= 6y.

Construction of Simple linear equations:-

7x + 3 = 17

Equation

o An equation, is always equated to either a numerical value or another algebraic expression.

o The equality sign shows that the value of the expression to the left of the ‘=’ sign is equal to the value of the expression to the right of the ‘=’ sign.

o In the above example, the expression 7x + 3 on the left side is equal to the constant 17 on the right side.

o The RHS may be an expression containing the variable. For example, the equation 7x + 3 = 3x − 1 has the expression 7x + 3 on the left and 3x − 1 on the right separated by an equality sign.

Solving an equation:-

· If the same number is added or subtracted on both sides of the equation, the value remains the same.

For example:-

x + 5 = 12, if 5 is subtracted on both sides, for separating the constants and variables of the equation,

That is,

x + 5 − 5 = 12 – 5

= x + 0 = 7,

Hence x = 7 [since 0 is the additive identity]

· If the same number is multiplied or divided on both sides of the equation, the equation remains the same.

For example,

If the equation 5y = 20, is divided by 5 on both sides.

Thus we have.

Therefore, y = 4.

· An equation remains the same, when the expressions on the left and on the right are interchanged.

The equation 7x + 3 = 17 is the same as 17 = 7x + 3. Similarly,

The equation 7x + 3 = 3x − 1 is the same as 3x −1 = 7x + 3.