Geometry

LINES:-

· A line extends along both directions without any end. A line AB is denoted by AB.

· A line segment has two end points. The line segment 'AB' is represented by .

· A Ray is a line that starts from a point 'A' and extends without any end in a particular direction passing through 'B' which is denoted by .

· If two lines m and n are parallel, then we denote it as m||n. Parallel lines never intersect each other.

· When two lines have a common point they are called intersecting lines and that point is called the point of intersection of the given two lines.

· If three or more points lie on the same line, then they are called collinear points; otherwise they are called non-collinear points.

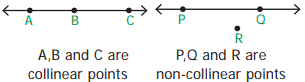
Angles:-

An angle is formed when two rays diverge from a common point. The rays forming an angle are called the arms of the angle and the common point is called the vertex of the angle.

§ An angle whose measure is less than 90° is called an acute angle.

§ An angle whose measure is exactly 90° is called a right angle.

§ An angle whose measure is greater than 90° is called an obtuse angle.

§ An angle whose measure is exactly 180° is called a straight angle.

§ An angle whose measure is greater than 180° and less than 360° is called a reflex angle.

§ Two angles are called Complementary angles if their sum is 90°.

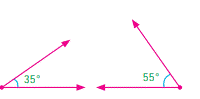
§ Two angles are called Supplementary angles if their sum is 180°.

Pair Of Angles Formed By Intersecting Lines:-

§ Adjacent angles:-

Two angles which have a common vertex and a common arm, whose interiors do not overlap are called adjacent angles.

For example:-

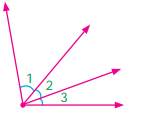
In this figure there are two pairs of adjacent angles such as ∠1, ∠2 and ∠2, ∠3 but the pair ∠1 and ∠3 are not adjacent because this pair of angles have a common vertex but they do not have a common arm as ∠2 is in between ∠1 and ∠3. Also interiors of ∠1 and ∠3 do not overlap. Since the pair of angles does not satisfy one among the three conditions they are not adjacent.

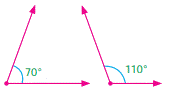
§ Linear pair:-

The adjacent angles that are supplementary lead us to a pair of angles that lie on straight line. This pair of angles are called linear pair of angles.

Example 1:

Which of the following pair of adjacent angles will make a linear pair?

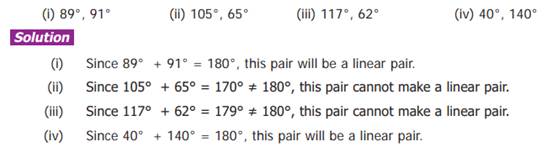
Example 2:- Two angles are in the ratio 3:2. If they are linear pair, find them.

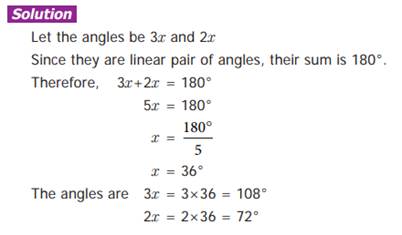
§ More on linear pairs:-

The sum of all the angles formed at a point on a straight line is 180°.

Example:-

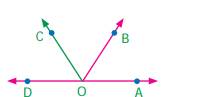
Here, ∠AOB + ∠BOC + ∠COD = 180°.

Example 1:- Find the measure of ∠ROS.

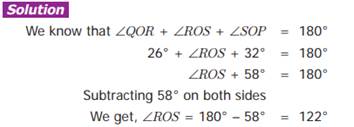
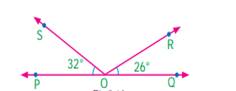
The sum of the angles at a point is 360°.

Example:-

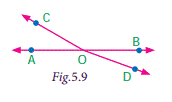
In the fig 5.9, AB is a straight line. OC is a ray meeting AB at O.

Here, ∠AOC and ∠BOC are linear pair. Hence ∠AOC + ∠BOC = 180°.

Also, OD is another ray meeting AB at O.

Again ∠AOD and ∠BOD are linear pair. Hence ∠AOD + ∠BOD = 180°.

Now, ∠AOC, ∠BOC, ∠AOD and ∠BOD are the angles that are formed at the point O. therefore,

(∠AOC + ∠BOC) + (∠AOD + ∠BOD) = 180° + 180° = 360°.

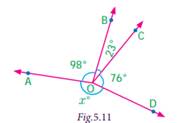
Example 1:- In Fig. 5.11, find the value of x°.

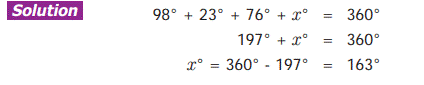
§ Vertically opposite angles:-

When two lines intersect each other, two pairs of non-adjacent angles formed are called vertically opposite angles.

§ Transversal:-

A transversal is a line that intersects two lines at distinct points.

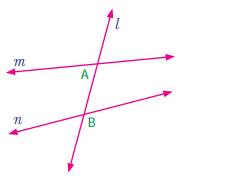
Angles formed by a transversal:-

If a transversal meet two lines, eight angles are formed at the points of intersection.

· Corresponding angles:-

All the pairs of angles having different vertices but lie on the same side (left or right) of the transversal (l), lie above or below the lines m and n are known as corresponding angles.

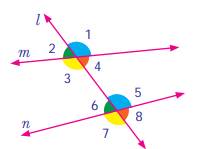
Here, the pairs of angles ∠1 and ∠5, ∠2 and ∠6, ∠3 and ∠7, ∠4 and ∠8 are the corresponding angles.

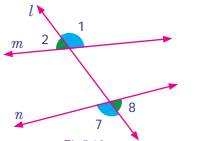
· Alternate Interior angles:-

Each of pair of angles named ∠3 and ∠5, ∠4 and ∠6 are marked on the opposite side of the transversal l and are lying between lines m and n are called alternate interior angles.

· Alternate Exterior angles:-

Each pair of angles named ∠1 and ∠7, ∠2 and ∠8 are marked on the opposite side of the transversal l and are lying outside of the lines m and n are called alternate exterior angles.

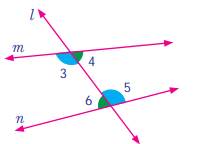
· Co-interior angles:-

Each pair of angles named ∠3 and ∠6, ∠4 and ∠5 are marked on the same side of transversal l and are lying between the lines m and n. These angles are lying on the interior of the lines m and n as well as the same side of the transversal l.

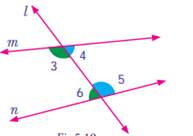
· Co-exterior angles:-

Each pair of angles named ∠1 and ∠8, ∠2 and ∠7 are marked on the same side of transversal l and are lying outside of the lines m and n. These angles are lying on the exterior of the lines m and n as well as the same side of the transversal l.

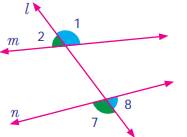
Angles formed by a transversal with Parallel lines:-

· When two parallel lines are cut by a transversal, each pair of corresponding angles are equal.

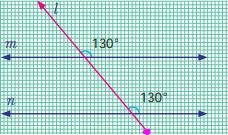
· When two parallel lines are cut by a transversal, each pair of alternate interior angles are equal.

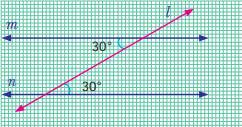
· When two parallel lines are cut by a transversal, each pair of alternate exterior angles are equal.

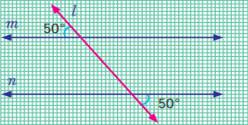
· When two parallel lines are cut by a transversal, each pair of interior angles that lie on the same side of the transversal are supplementary.

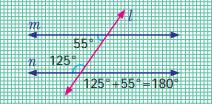
· When two parallel lines are cut by a transversal, each pair of exterior angles that lie on the same side of the transversal are supplementary.

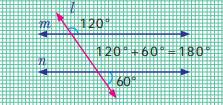
Example 1:- If l is parallel to m, find the measure of x and y in the figure.

Example 2:-

Construction:-

Construction means to draw lines, angles and shapes accurately.

· Construction of perpendicular bisector of a line segment

A perpendicular line which divides a line segment into two equal parts is a perpendicular bisector of the given line segment.

Example: - Construct a perpendicular bisector of the line segment AB = 6 cm.

· Construction of angle bisector of an angle:-

If a line or line segment divides an angle into two equal angles, then the line or line segment is called angle bisector of the given angle.

Example: - Construct bisector of the ∠ABC with the measure 80°.

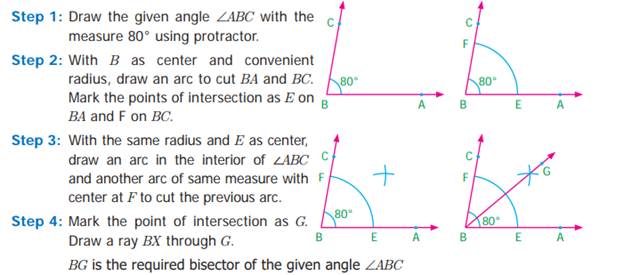
Construction of special angles without using protractor:-

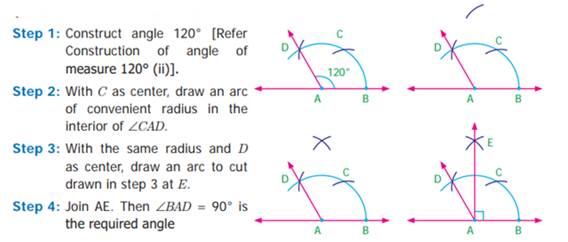
1. Construction of angle of measure 60°

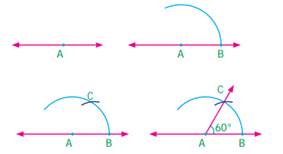
2. Construction of angle of measure 120°

Since, two 60° make 120°

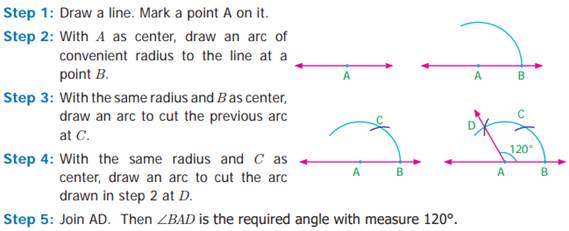
3. Construction of angle of measure 30°

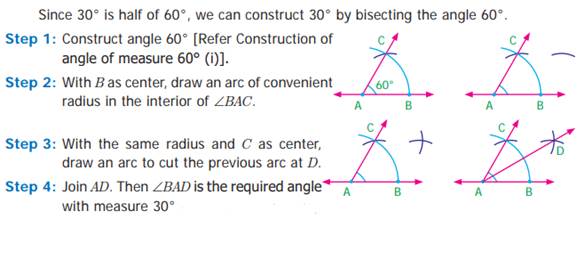
4. Construction of angle of measure 90°