Number System
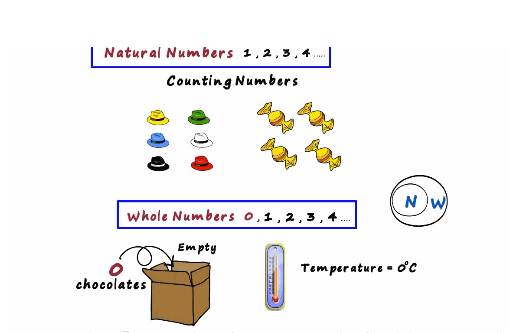
![]() Integers
are a collection of natural numbers, zero and negative numbers.
Integers
are a collection of natural numbers, zero and negative numbers.
![]() Integers
are denoted by Z
Integers
are denoted by Z
![]() Integers
can be represented by using a number line
Integers
can be represented by using a number line
![]() In
a number line, zero occupies the central position, separating positive and negative
integers.
In
a number line, zero occupies the central position, separating positive and negative
integers.

![]() To
the left of zero lies the negative integers and to the right of zero lies
positive integers.
To
the left of zero lies the negative integers and to the right of zero lies
positive integers.
![]() In
a number line, integers are placed in an increasing order from left to right.
In
a number line, integers are placed in an increasing order from left to right.
For example: -3, -2, -1, 0, 1, 2, 3 are in ascending
order.
![]() Moving
along the left, integers are arranged in decreasing order
Moving
along the left, integers are arranged in decreasing order
For example: Among -10, -9, -8, -7 etc,
-7 > -8 > -9 > -10 is the order.
Among -65 and 65, 65 > -65 is the order.
1.
Write the following integers in ascending order:
-5, 0, 2, 4, -6, 10,-1, -6, -5, -1, 0, 2, 4,
10 is the order.
2.
If the integers 15, 12, 17, 5, 1, 5, 6 are marked on the number line
then the integer on the extreme left is:-17
3. Write the given integers in descending order:
27, 19, 0, 12, 4, 22,
47, 3, 9, 35, 47, 19, 12, 3, 0, -4, -9, -22, -27, -35
Addition
of integers
![]() Addition
of integers can be done by using the number line.
Addition
of integers can be done by using the number line.
![]() To
add (+5) and (3), we start at five. Then, we move three steps backwards (since
3 has sign) We reach +2, which is the answer
To
add (+5) and (3), we start at five. Then, we move three steps backwards (since
3 has sign) We reach +2, which is the answer
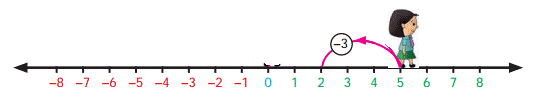
![]() We
can also do this by starting at -3 in the number line and move five steps
forward. We reach +2, which is the answer
We
can also do this by starting at -3 in the number line and move five steps
forward. We reach +2, which is the answer
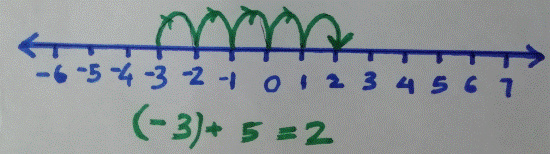
![]() Similarly,
to add (-6) and (-4), We can start at (-6) and move 4
steps backward (since four has negative sign). We can also start at (-4) and move six step
backward to get the same answer.
Similarly,
to add (-6) and (-4), We can start at (-6) and move 4
steps backward (since four has negative sign). We can also start at (-4) and move six step
backward to get the same answer.
We get -10, which is the answer.
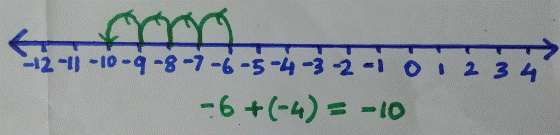
![]() To
add (-6) and 4, we start at -6 and move four steps forward to reach (-2), which
is the answer.
To
add (-6) and 4, we start at -6 and move four steps forward to reach (-2), which
is the answer.
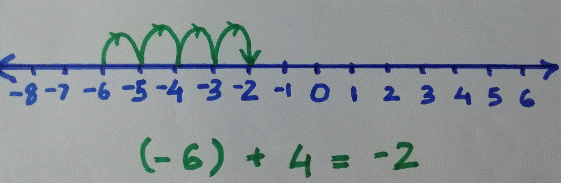
Examples
Add 10 and -15
Start at 10 on number line and move 15
steps backward. We get (-5) which is the answer.
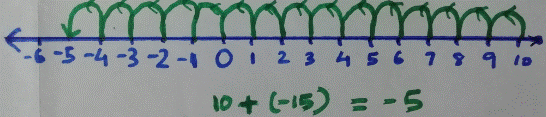
Add (-7) and (-9)
Start at -7 and move 9 steps backward. We
get (-16) which is the answer.
Rules for addition of
integers
1. The
integer without sign represents positive integer.
For eg:
9represents (+9), 27 represents (+27), etc.
2. When
we add two integers of the same sign, the sum will also be an integer of the
same sign.
Add (-70) and (-12)
To add (-70)
and (-12), we add the two numbers 70 + 12 =82) and we put the sign (here, -
sign). Hence, (-82) is the answer.
Add 103 and 39
103 + 39 = 142
3. When
we add two integers of different sign, the sum will be the difference between
the two integers and have the sign of the integer with greater value.
For eg: While adding (-7) and (+4) the answer is (-3)
which is the difference between 7 and 4 with the sign of the greater number, 7.
Ie. Negative sign.
Examples
Add (-40) and 30
To add (-40) and 30, we find the difference
between the two numbers (40 30 =10) and we put the sign of the greater number
(here, - sign). Hence, -10 is the answer.
Add 60 and (50)
To
add 60 and (-50), we find the difference between the two number (60 50 =10)
and we put the sign of the greater number ( here, +
sign).
Hence, +10 is the answer.
Word
problems
1.
Sita
saved Rs. 225.00 and she has spent Rs. 400 on credit basis for the purchase of
stationery. Find her due amount?
The
amount Sita has = 225 Rs
The
amount spent for stationery on credit = 400 Rs
The due
amount to be paid = 225 400 = 175
Rs
Therefore, Sita has to pay Rs 175
Properties
of Addition of integers
1. Closure property
![]() The
sum of two integers is an integer. This property is called closure property.
The
sum of two integers is an integer. This property is called closure property.
![]() Since
integers obeys closure property, we can say that integers are closed under
addition.
Since
integers obeys closure property, we can say that integers are closed under
addition.
For eg: The sum of -12 and +12
gives zero, which is also an integer.
![]() Therefore,
for any two integers a and b, (a + b) is also an integer.
Therefore,
for any two integers a and b, (a + b) is also an integer.
2. Commutative property
![]() The
order in which we add two integers does not matter. This is called commutative
property.
The
order in which we add two integers does not matter. This is called commutative
property.
For eg: (-39) + 32 and 32 + (-39) gives the same answer, (-7)
(-8) + (-18) and (-18) + (-8) gives same answer, (-26)
![]() Therefore,
for any two integers, a and b, a
+ b = b + a
Therefore,
for any two integers, a and b, a
+ b = b + a
3. Associative property
![]() Regrouping
of integers does not change the value of their sum. This property is called
associative property.
Regrouping
of integers does not change the value of their sum. This property is called
associative property.
For eg: Take (-5), (-9) and 13. Now, let us group them in different way
[(-5)
+ (-9)] + 13 and (-5) + [(-9) + (13)]
[(-5) + (-9)] + 13 =
[(-14)] + 13 = -1
(-5) + [(-9) + (13)] = (-5) + [(4)] =
-1
Both of the cases give same answer. Hence, integers
obey associative property.
![]() Therefore,
for any three integers a, b, and
c, a + ( b +c ) = ( a
+ b) + c
Therefore,
for any three integers a, b, and
c, a + ( b +c ) = ( a
+ b) + c
4. Additive identity
![]() Adding
zero to any integer gives the same integer. Due to this property, zero is
called the identity with respect to addition or additive identity.
Adding
zero to any integer gives the same integer. Due to this property, zero is
called the identity with respect to addition or additive identity.
For eg: 0 + 99 = 99,
0 + (-27) = -27, 0+ (85) =
(85)
![]() Therefore,
for any integer a, a + 0 = 0 + a = a
Therefore,
for any integer a, a + 0 = 0 + a = a
5. Additive inverse
![]() The pair of opposite integers, whose
sum is zero is called additive inverse.
The pair of opposite integers, whose
sum is zero is called additive inverse.
![]() In a number line, additive inverses are
equidistant from zero.
In a number line, additive inverses are
equidistant from zero.
For example: (-17) and +17, (-5)
and 5, (8) and (-8) are additive inverses of each other.
![]() Therefore,
for any integer a, a is the additive inverse.
Therefore,
for any integer a, a is the additive inverse.
A+ (a) = (a) +a = 0

Subtraction of integers
![]() Subtraction
of integers can be done using the number line.
Subtraction
of integers can be done using the number line.
![]() For
subtraction, we move backward in a number line. But, when two (-) signs come
next to each other, we move forward.
For
subtraction, we move backward in a number line. But, when two (-) signs come
next to each other, we move forward.
![]() To
subtract (+4) from (+7), we start at 7 and move four steps backward to reach (+3),
which is the answer.
To
subtract (+4) from (+7), we start at 7 and move four steps backward to reach (+3),
which is the answer.
Subtract (6) from (-9)
(-9) - (6), we start
at (-9) and move six steps backward to reach (-15), which is the answer.
Subtract (-5) from (-8)
(-8) (-5). We start
at (-8) and move five steps forward ( we
move forward when two negative signs come next to each other). We reach (-3),
which is the answer.
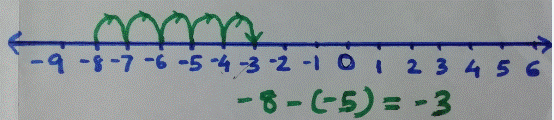
Subtract (-7) from (8)
8 (-7) We start at 8 and move 7 steps forward, to reach
15, which is the answer
Rules for subtraction of integers
1.
To
subtract a negative integer from a negative integer, we add the additive
inverse of the integer to be subtracted.
For
eg: Subtract (-3) from 7
7
(-3)
Add the additive inverse of (-3), ie +3
= 7 +3
= 10
Find the values of: (6)(2), 26 (+10), 35 + (7)
(a)
-6 (-2) = -6 +2
= -4
(b)
26 (+10) = 26 -10
= 16
(c)
35 + (-7)
= 35 7
=28
Note
![]() Every
subtraction statement has a corresponding addition statement.
Every
subtraction statement has a corresponding addition statement.
For
example, 8 5 = 3 is a subtraction statement. This can be seen as the addition statement 3 + 5 = 8
![]() In
the same way, (-8) (-5) = (-3)
is a subtraction statement which can be written as the addition
statement (-8) = (-3) + (-5)
In
the same way, (-8) (-5) = (-3)
is a subtraction statement which can be written as the addition
statement (-8) = (-3) + (-5)
Properties
of Subtraction of integers
1.
Closure property
![]() The
difference of two integers is an integer. This property is called closure
property.
The
difference of two integers is an integer. This property is called closure
property.
![]() Since
integers obey closure property, we can say that integers are closed under
subtraction.
Since
integers obey closure property, we can say that integers are closed under
subtraction.
For eg: The difference between (-7) and (-2) gives
(-5), which is also an integer.
![]() Therefore,
for any two integers, a and b; ab is also an integer.
Therefore,
for any two integers, a and b; ab is also an integer.
![]() The
commutative and associative properties do not hold for subtraction.
The
commutative and associative properties do not hold for subtraction.
Multiplication
of Integers
![]() Multiplication
of negative integers is also repeated addition just like positive integers or
whole numbers.
Multiplication
of negative integers is also repeated addition just like positive integers or
whole numbers.
For
eg: [(-5) + (-5) + (-5)] can be
represented as (-5) ื (-3)
![]() The
following number line shows this
The
following number line shows this

![]() The
product of two negative integers is always a positive integer.
The
product of two negative integers is always a positive integer.
For eg: (-8) ื (-6) = 48, (-9) ื− (-9) = 81
![]() The
product of a positive and negative integer is a negative integer
The
product of a positive and negative integer is a negative integer
For eg: (-5) ื (7) = (-35), (4) ื (-5) = (-20)
Which
of the following is incorrect?
a.
-55
ื -22 ื -33 < 0 b. (-1521) ื 2511 > 0
A is correct as the product of two negative
numbers is positive. The
Product of that positive and negative
number is a negative (less than 0)
b is incorrect as the product of a positive and
negative number is always negative (less than 0)
Properties
of multiplication of integers
1. Closure property
![]() The
product of two integers is an integer. Therefore, integers are closed under
multiplication.
The
product of two integers is an integer. Therefore, integers are closed under
multiplication.
For eg: (-9) ื
5 = (-45), which is also an integer
(-6) ื
(-6) = (-36), which is also an integer
![]() Therefore,
for any two integers a and b; a ื b is also an integer.
Therefore,
for any two integers a and b; a ื b is also an integer.
2. Commutative property
![]() Changing
the order of multiplication does not change the value of the product.
Changing
the order of multiplication does not change the value of the product.
![]() Thus,
multiplication of integers is said to be commutative.
Thus,
multiplication of integers is said to be commutative.
For
eg: 21 ื (-5) = (-105), (-5) ื 21 =
(-105)
(-8) ื
(-9) = 72, (-9) ื (-8) = 72
In both
cases, we get same answer, even though order is changed.
![]() Therefore,
for any two integers a and
b, a ื b = b ื a
Therefore,
for any two integers a and
b, a ื b = b ื a
3. Associative property
![]() Re
grouping of integers does not change the value of their product. This property
is called associative property.
Re
grouping of integers does not change the value of their product. This property
is called associative property.
For eg: [(-5) ื7] ื (-18) and (-5) ื [7ื (-18)] are equal
[(-5)
ื7] ื (-18) = [-35] ื (-18) = 630
(-5)
ื [7ื (-18)] = (-5) ื [126] = 630
Therefore, for any three integers a, b, c, (a ื b) ืc = aื (b
ื c)
4. Multiplicative identity
![]() Multiplying
one with any integer gives the same integer. Therefore, 1 is called
multiplicative identity.
Multiplying
one with any integer gives the same integer. Therefore, 1 is called
multiplicative identity.
For eg: 1ื (-7) = (-7) ื1 = (-7), 57 ื1 = 1ื 57 = 57
![]() Therefore,
for any integer a, aื1 = 1ืa =a.
Therefore,
for any integer a, aื1 = 1ืa =a.
Note
![]() The
product of odd number of negative integers is negative.
The
product of odd number of negative integers is negative.
Eg: (-3) ื (-4) ื (-6) = (-72), (-2) ื (-4) ื (-6) = (-48)
(-1) ื (-3) ื (-5) ื (-7) ื (-9) =
(-105)
![]() The
product of even number of negative integers is positive.
The
product of even number of negative integers is positive.
For eg: (-6) ื (-7) = 42, (-1) ื (-3) ื (-5) ื (-7) = 105
(-1) ื (-1)
ื (-1) ื (-1) = +1
![]() Generally, if negative integers are
multiplied even number of times, the product is a positive integer, whereas, if
negative integers are multiplied odd number of times, the product is a negative
integer.
Generally, if negative integers are
multiplied even number of times, the product is a positive integer, whereas, if
negative integers are multiplied odd number of times, the product is a negative
integer.
Distributive property of multiplication
over addition
![]() For
integers, multiplication is distributive over addition.
For
integers, multiplication is distributive over addition.
For eg: (-2) ื
(4+5) = [(-2) ื4] + [(-2) ื5]
LHS = (-2) ื (4+5) RHS = [(-2) ื4] + [(-2) ื5]
= (-2) ื (9) = [-8] + [-10]
= -18 = -18
LHS
= RHS. Therefore, multiplication distributes over addition for integers.
![]() Therefore,
for any three integers a, b, and c , a ื
(b+c) = (a ื b) + (aืc)
Therefore,
for any three integers a, b, and c , a ื
(b+c) = (a ื b) + (aืc)
Word
problems
1.
During
summer, the level of the water in a pond decreases by 2 inches every week due
to evaporation. What is the change in the level of the water over a period of 6
weeks?
Change in level of water in
one week = -2 inches
The change in level of water
after six weeks = (-2) ื6 = -12 inches
Therefore, the level of water
decreases by 12 inches after 6 weeks
Division of integers
![]() The
rules for division of integers is similar to that of multiplication
The
rules for division of integers is similar to that of multiplication
![]() To
divide integers with same sign, divide as usual and put the sign.
To
divide integers with same sign, divide as usual and put the sign.
![]() The
division of two integers with the same sign gives a positive integer
The
division of two integers with the same sign gives a positive integer
For eg: 72 ๗ 9 = 8, (-60) ๗ (-12) = 5
![]() To divide integers with opposite sign,
divide as usual and put negative sign.
To divide integers with opposite sign,
divide as usual and put negative sign.
![]() The division of two integers with
opposite signs gives a negative integer
The division of two integers with
opposite signs gives a negative integer
For
eg: (-81) ๗3 = (-27), 50 ๗
(-5) = (-10)
Properties
of division
![]() Integers
are not closed under
division.
Integers
are not closed under
division.
For eg:
(-7) ๗5 is a fraction and is not an integer. Similarly, 9 ๗ (-5) is not
an integer.
![]() Integers
are not commutative under division.
Integers
are not commutative under division.
For
eg: (-14) ๗ 7 = (-2), but 7 ๗ (-14)
≠ (-2) similarly, 15 ๗ 5 ≠ 5๗ 15
![]() Integers
are not associative under division.
Integers
are not associative under division.
For eg: [(-12 ๗2)] ๗3 and (-12) ๗ [(2๗3)] are not
equal.
Similarly, [9๗ (-3)] ๗ 3 and 9๗ [(-3)
๗3] are not equal.
![]() There
is no identity element for integers under division
There
is no identity element for integers under division
For
eg: Take the case of 1. 7๗1 = 7, but 1๗7 ≠ 7
Note
![]() Each
multiplication statement has two division statements in whole numbers.
Each
multiplication statement has two division statements in whole numbers.
For
eg: The multiplication statement 8ื9 = 72
has 72๗ 8 = 9 and 72๗ 9 =8 as division statements.
![]() An
integer divided by zero is not defined, but zero divided by any number is zero.
An
integer divided by zero is not defined, but zero divided by any number is zero.
For eg:
1๗ 0 is not defined, but 0 ๗1 = 0
1. An
elevator descends into a mine shaft at the rate of 5 m/min. If the descent
starts from 15 m above the ground level, how long will it take to reach - 250 m?
Rate of
descent of mine shaft = 5 m/min
Starting position of the shaft = 15 m above the ground
Final
position of the shaft = 250 m below the ground
To
reach -250 m, the shaft has to descend 15 m below to reach ground
Level, and then descend 250 m below ground
level.
Therefore,
total distance = 250 + 15 = 265 m
Time taken
= ![]()
= ![]() = 53
= 53
Therefore,
the shaft takes 53 minutes to reach (-250) m.

Summary
![]() Integers
are a collection of natural numbers, zero and negative numbers.
Integers
are a collection of natural numbers, zero and negative numbers.
![]() The
number line gives a visual representation of the set of all integers with
positive integers to the right of zero and negative integers to the left of
zero.
The
number line gives a visual representation of the set of all integers with
positive integers to the right of zero and negative integers to the left of
zero.
![]() The
sum of the two positive integers is positive and two negative integers is
negative
The
sum of the two positive integers is positive and two negative integers is
negative
![]() The
sum of a positive and a negative integer is the difference of the two numbers
in value and has the sign of the greater integer.
The
sum of a positive and a negative integer is the difference of the two numbers
in value and has the sign of the greater integer.
![]() The
addition of integers has the closure, commutative and associative properties
The
addition of integers has the closure, commutative and associative properties
![]() The
product of two positive integers and two negative integers are positive
The
product of two positive integers and two negative integers are positive
![]() The
product of two integers with opposite signs is negative
The
product of two integers with opposite signs is negative
![]() The
multiplication of integers has the closure, commutative and associative properties
The
multiplication of integers has the closure, commutative and associative properties
![]() The
integer 0 is the additive identity for integers.
The
integer 0 is the additive identity for integers.
![]() The
integer 1 is the multiplicative identity for integers
The
integer 1 is the multiplicative identity for integers