Algebra

Exponents and Powers:

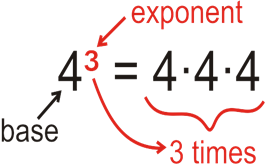
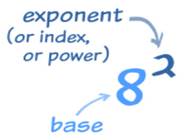
We can write large numbers in simplified form as given below. For example, 16 = 8 x 2 = 4 x 2 × =2 x 2 x 2 x 2 x 2 Instead of writing the factor 2 repeatedly 4 times, we can simply write it as 24 . It can be read as 2 raised to the power of 4 or 2 to the power of 4 or simply 2 power 4. This method of representing a number is called the exponential form. We say 2 is the base and 4 is the exponent. The exponent is usually written at the top right corner of the base and smaller in size when compared to the base.

Let us look at some more examples

Ø 64= 4×4×4= (base is 4 and exponent is 3)

Ø 64 =8× 8=(base is 8 and exponent is 2)

Ø 243=3×3×3×3×3= (base is 3 and exponent is 5)

Ø 125 =5×5××5 = (base is 5 and exponent is 3)

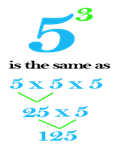
Remember, when a number is expressed as a product of factors and when the factors are repeated, then it can be expressed in the exponential form. The repeated factor will be the base and the number of times the factor repeats will be its exponent. We can extend this notation to negative integers also.

For example:

− 125 =(- 5)×(-5)×(-5) = [base is ‘ −5 ’ and exponent is 3] Hence, ( ) −5 3 is the exponential form of −125 .

Numbers in Exponential Form:

Now, we will see how to express numbers in exponential form. Let us take any integer as ‘a’.

Then, a = a1 [‘a power 1’]

a× a = a 2 [‘a power 2’ ; ‘a’ is multiplied by itself 2 times]

a×a×a = a3 [‘a power 3’ ; ‘a’ is multiplied by itself 3 times]

………………………………………………………………………………………….

…………………………………………………………………………………………

a× a× …….×a( n times)= "[‘a power n’ ; ‘a’ multiplied by itself n times]K

Thus we can generalize the exponential form as an , where the exponent is a positive integer ( ) n > 0 .

Observe, the following examples.

100= 10× 10=

This can also be expressed as the product of two different bases with the same exponent as, 100= 25 4= (5× 5)×( 2× 2)

We notice that 5 and 2 are the bases and 2 is the exponent.

In the same way, a × a × a × b× b = "

Consider, 35=

where there is no repetition of factors. Thus, usually is represented as 7×5. So, when the power is 1 the exponent will not be explicitly mentioned.

Laws of Exponents

Let us learn some rules to multiply and divide exponential numbers with the same base.

Multiplication of Numbers in Exponential form

Let us calculate the value of 23 × 22

Solution:

×

= (2 × 2 × 2) × (2 × 2)

= 2 × 2 × 2 × 2 × 2

=

=2³⁺²

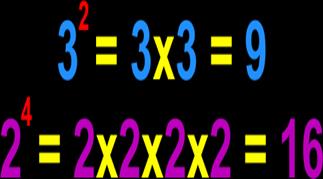
We observe that the base on 23 and 22 is the same 2 and the sum of the powers is 5. Now, let us consider negative integers as the base.

(−3)3 × (−3)2 = [(−3) × (−3) × (−3)]×[(−3) × (−3)]

= (−3) × (−3) × (−3) × (−3) × (−3)

= (−3)5

= (−3)

We observe that the base of (−3)3 and (−3)2 is the same as (−3) and the sum of the power is 5. Similarly, p4 × p2 = (p × p × p × p) × (p × p) = p6 = p4+2

Now, for any non-zero integer ‘a’ and whole number ‘m’ and ‘n’, consider and

That is , = a × a × a × ... × a (m times) and

= a × a × a × ... × a (n times)

So, × = a × a × a × ... × a (m times) ×a × a × a × ... × a (n times)

= a × a × a × ... × a (m+n times) =

Therefore, × =

This is called Product Rule of exponents.

Example

Simplify using Product Rule of exponents.

(i) × (ii) × × (iii) 25 × 32 × 625 × 64

Solution:

(i) ×

= +3 [since, a] × =

= 510

(ii) × × = × = ×

=

=

(iii) 25 × 32 × 625 × 64 = (5 × 5) × (2 × 2 × 2 × 2 × 2) ×(5 × 5 × 5 × 5) × (2 × 2 × 2 × 2 × 2 × 2)

= ×××

= × )×(× )[grouping exponential numbers]

= ×

= ×

Division of Numbers in Exponential form

1. Let us calculate the value of

Solution:

==

=

=

We observe that the base of and is the same ‘2’ and the difference of powers is 3. Now, let us consider negative integers as the base.

Consider ,

=

=

We observe that the base of (and (is the same as (–5) and the difference of the power is 1.

Thus, we can observe that for any non-zero integer ‘a’ and for whole numbers ‘m’and ‘n’, consider and , m> n .

= a × a × a × ... × a (m times)

= a × a × a × ... × a (n times)

=

= a×a×a×….×a(m-n)times

=

This is called Quotient Rule of exponents.

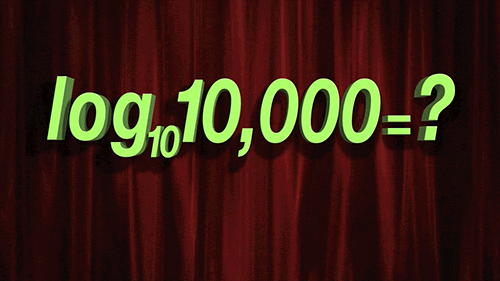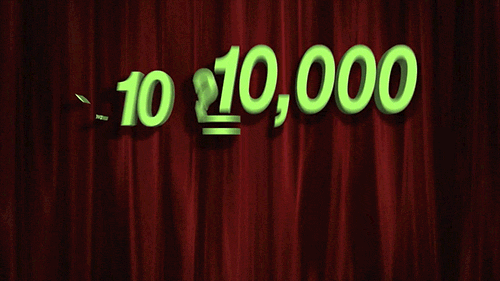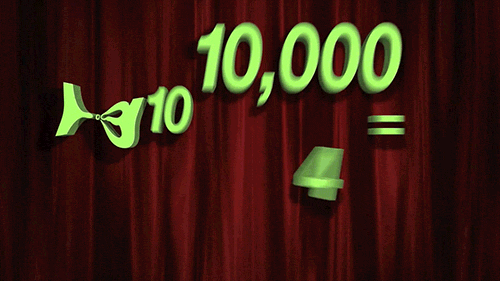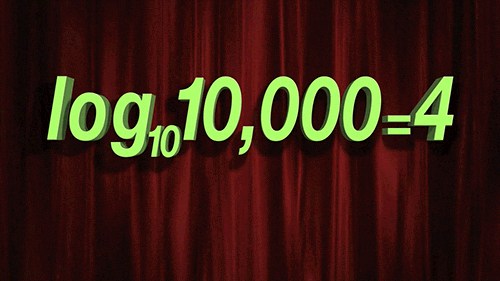
Exponent Numbers with Different Base and Same Power

1. To understand the multiplication of exponent numbers with different base and

same powers, let us consider the following example,

105 = 10 ×10 ×10 ×10 ×10

= (2 × 5) × (2 × 5) × (2 × 5) × (2 × 5) × (2 × 5)

= (2 × 2 × 2 × 2 × 2) × (5 × 5 × 5 × 5 × 5)

105 = 25 × 55

But we know that, 10 = 2 × 5. Hence 105 = (2 × 5)5 = 25 × 55 .

In general, for any non-zero integers ‘a’ and ‘b’ and for whole number ‘m’ (m> 0),

= a × a × a × ... × a (m times) × b × b × b × ... × b (m times)

= (a × b) × (a × b) × (a × b) × ... × (a × b) (m times) = (a × b)m

Therefore, =(a×b)

2. To understand the division of exponent numbers with different base and same

powers, let us consider the following example

10 ×10 × 10 × 10 ×10

=())))

=

Therefore /

But we know that, 10 =

=)2

Hence, for any two non-zero integers ‘a’ and ‘b’ and a whole number ‘m’ (m> 0),

) =)×))) (m times)

=

=

Problems

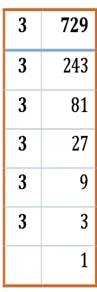
1. Express 729 in exponential form.

Solution:

Dividing by 3, we get 729= 3×3×3×3×3×3 =

Also, 729= 9×9×9=

2. Express the following numbers in exponential form with the given base:

(i) 1000, base 10 (ii) 512, base 2 (iii) 243, base 3.

Solution:

(i) 1000 = 10 ×10 × 10 =

(ii) 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 =

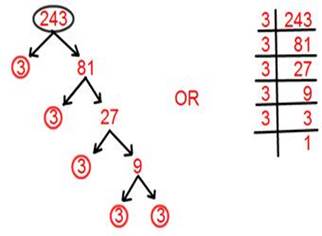
(iii) 243 = 3 × 3 × 3 × 3 × 3 =

3. Find the value of (i) 132 (ii) (−7)2 (iii) (−4)3

S Solution:

IoNOTE:

(–1)n =1, if n is an even natural number.

(–1)n =–1, if n is an odd natural number

(i) 132 = 13 ×13 = 169

(ii) (−7)2 = (−7) × (−7) = 49

(iii)(−4)3 = (−4) × (−4) × (−4) = 16 × (−4) = −64

4. Find the value of 23 + 32

Solution:

23 + 32 = (2 × 2 × 2) + (3 × 3)

= 8 + 9 = 17

5. Which is greater 34 or 43?

Solution :

34 = 3 × 3 × 3 × 3 = 81

43 = 4 × 4 × 4 = 64

81> 64 gives 34 > 43

Therefore, 34 is greater.