Information Processing
Introduction:
In
general days, we may observe patterns in both nature and man-made things. In
nature, patterns seem in tress, leaves, movements in celestial bodies and many
others. In man-made. Patterns occurs in structures, buildings, and many more.
It is really wonder to know all beautiful patterns are based on mathematics.
We have
to find the relationship between the different types of patterns and
structures; E.g. patterns in fabric designs,

Tables and patterns leading to
linear functions
Situation 1: Observe
the pattern carefully,

Consider the circular disc, now
observe the pattern of shapes in the tabular form;
|
Number of steps (x) |
1 |
2 |
3 |
4 |
….. |
|
Number of circular ring (y) |
1 |
3 |
5 |
7 |
…… |
Here, you find the relationship
between the number of steps and number of circular rings in each step. So, the
relation between the variable assumed x and y can be generalised as y=2x-1.
Example 1: In the
following figures, polygons are formed by increasing the number of sides using
matchsticks as given below.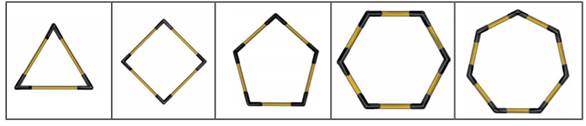
Find the number of sticks
required to form the next three shapes by tabulation and generalisation?
Solution:
In the above pattern of polygons, in the first
shape (x = 1), we get a closed shape called a triangle. Similarly, the second
shape (x = 2) gives a four-sided polygon and the third shape (x = 3) is a
five-sided polygon and continuing in the same way two more shapes are formed.
If the number of match sticks required to form each of the shapes is taken as
y, then the values of x and y are tabulated as given below.
|
X |
1 |
2 |
3 |
4 |
5 |
….. |
|
y |
3 |
4 |
5 |
6 |
7 |
…… |
Observe the table given above;
when x = 1, y
= 3 = 1+2
when x = 2, y
= 4 = 2+2
when x = 3, y
= 5 = 3+2
when x = 4, y
= 6 = 4+2
when x = 5, y
= 7 = 5+2
Hence, each of the values of y which we get from
the table is 2 more than x. That is y x = + 2.
Therefore, 6th shape (x=6) will have y = 8 = 6+2
(8 match sticks) and so on.
Some Problems:
1. Write the
appropriate number of pattern and its generalisation:
(i)

(ii)
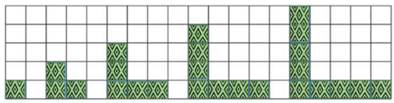
2. Identify
the correct relationship between x and y from the given table
|
X |
1 |
2 |
3 |
4 |
…… |
|
Y |
4 |
8 |
12 |
16 |
…… |
(i)
Y=4x
(ii)
y =x + 4
(iii)
y = 4
(iv)
y =4 * 4
3. Identify
the correct relationship between x and y from the given table
|
X |
-2 |
-1 |
0 |
1 |
2 |
…… |
|
Y |
6 |
3 |
0 |
-3 |
-6 |
…… |
(i)
y =x−2
(ii)
y = x+2
(iii)
y= x +3
(iv)
y = -3x
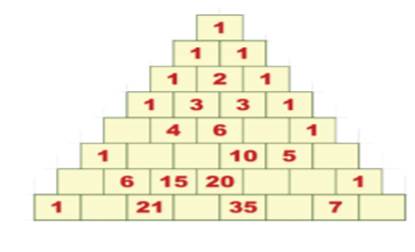
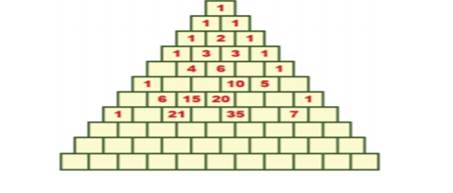
Pascal’s triangle
It is a triangular array of the binomial coefficients.
Write a function that takes an integer value n as input and prints first n
lines of the Pascal’s triangle. Following are the first 6 rows of Pascal’s
Triangle.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
I.e. also,
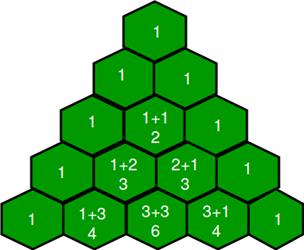
Example: Complete
the following Pascal’s Triangle by observing the number pattern.
Solution:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Example: Observe
the sequence of numbers obtained in the 3rd and 4th slanting rows of Pascal’s
Triangle and find the difference between the consecutive numbers and complete
the table given below.
(i)
|
3rd slanting row |
1 |
3 |
6 |
10 |
15 |
21 |
|
difference |
|
2 |
------ |
4 |
----- |
6 |
Sol: 2, 3, 4, 10, 6
(ii)
|
4th slanting row |
1 |
4 |
10 |
20 |
35 |
|
Difference |
|
3 |
------ |
10 |
------ |
Sol: 3, 6, 10, 15.
Example: Tabulate
the 3rd slanting row of the Pascal’s Triangle by taking the position of the
numbers in the slanting row as x and the corresponding values as y.
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
---- |
|
y |
1 |
3 |
6 |
10 |
15 |
21 |
---- |
Verify whether the relationship,
y= ![]() between x
and y for the given values is true.
between x
and y for the given values is true.
Solution: Observe
the table carefully. To verify the relationship between x and y, let us
substitute the values of x and get the values of y.
If x=1, then y=1; y= ![]() =
= ![]() = 1
= 1
If x=2, then y=3; y= ![]() =
= ![]() =3
=3
If x=3, then y=6; y= ![]() =
= ![]() =6
=6
If x=4, then y=10; y= ![]() =
= ![]() =10
=10
If x=5, then y=15; y= ![]() =
= ![]() =15
=15
If x=6, then y=21; y= ![]() =
= ![]() =21
=21
Note: The values of y are
obtained by half of the product of the two consecutive values of x.
Hence, y =![]() is
verified.
is
verified.
Problems based on
this concept:
1. Complete
the Pascal’s Triangle.
2. The
following hexagonal shapes are taken from Pascal’s Triangle. Fill in the
missing numbers.

3. What is
the sum of the elements of ninth row in the Pascal’s Triangle?
(i)
128
(ii)
254
(iii)
256
(iv)
126
4. The
difference between the consecutive terms of the fifth slanting row containing
four elements of a Pascal’s Triangle is
(i)
3,6,10,…
(ii)
4,10,20,…
(iii)
1,4,10,…
(iv)
1,3,6,…
5. Verify
whether the following hexagonal shapes form a part of the Pascal’s Triangle.
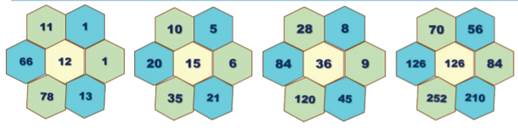
Solution:
1.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210
252 210 120 45 10 1
(i)
13 1
91 14 1
105 1
(ii)
20 15
35 35 21
70 56
(iii)
120 210
165 330 462
495 792
(iv)
18 153
19 171 462
190 1140
2.
Answer.
3.
(iii) 256
4.
(ii) 4, 10, 20,…….
5.
(i)
1*13*66 = 11*1*78
(ii)
5*12*20 = 10*6*35
(iii)
8*45*84 = 28*9*120
(iv)
56*210*126 = 70*84*252