Measurements
1 Introduction
The closed shapes such as
rectangle and square having area and perimeter. Pasting of tiles on a wall,
paving a parking lot with stones, fencing a field or ground etc., are some of the
places where the knowledge of area and perimeter of rectangle are essential. Lets extend this concept to
circles. The best example of a circle is the wheel. The invention of wheel is
perhaps the greatest achievement of mankind.

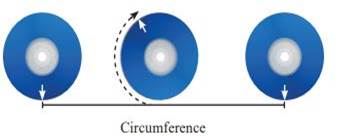
The distance covered by the wheel
when it rotates once. How do we measure the distance around the circle?
We cannot measure the curves with
the help of a ruler, as these shapes do not have straight edges. But there is a
way to measure the distance around the circle. Mark a point on its boundary.
Place the wheel on the floor in such a way that the marked point coincides with
the floor. Take it as the initial point. Rotate the wheel once on the floor
along a straight line till the marked point again touches the floor. The distance
covered by it is the distance around the outer edge of a circle. That is,
circumference.
We are now going to discuss the circumference and
area of the circle.

2 Circle
In our daily life, we come across
circular shapes in various places. For understanding of circular shapes, first
let us see how to trace a circle through an activity.
Put a pin on a board, put a loop
of string around it, and insert a pencil into the loop. Keep the string
stretched and draw with the pencil. The pencil traces out a circle.

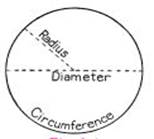
The position of the pin on the
board is the centre (O) of the circle. The length of the string is the radius
(r) of the circle.
While tracing a circle, the two
positions of the string which falls on a straight line is the diameter (d) of
the circle. It is twice the radius (d = 2r).
3 Circumference of a Circle
All circles are similar to one
another. So, the ratio of the circumference to that of diameter is a constant,
that is
![]()
Its approximate value is 3.14. Therefore
![]() .
.
The diameter is twice the radius (2r), so the
above equation can be written as ![]()
Therefore, the circumference of circle, ![]() units.
units.
Obviously now, we see that
Circumference, ![]() and d r = 2 .
and d r = 2 .
Thus for any circle with a given ‘r’ or ‘d’, we can find ‘C’ and vice-versa
Example 1
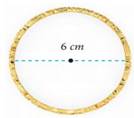
Calculate the
circumference of the bangle shown in Fig. 2.5 (Take π = 3 1. 4 ).
Solution
Given,
d = 6 cm , d
=2r = 6 cm, r = 3 cm
Circumference
of a circle = 2πr
= 2 π× r = 18.84
The
circumference is 18.84 cm.
Example 2
What
is the circumference of the circular disc of radius 14 cm? (use
π = 22/7 )
Solution
Radius
of circular disc ( r) = 14 cm
Circumference
of the disc = 2πr units
= 2×22/7×14
= 88cm
Example 3
If
the circumference of the circle is 132 m. Then calculate the radius and
diameter
(Take π = 22/7 ).
Solution
Circumference
of the circle, C = 2πr units
The
circumference of the given circle = 132 m
![]()
![]()
![]()
d
= 2r
d=
2× 21 = 42 m
Example 4
What
is the distance travelled by the tip of the seconds hand of a clock in 1
minute, if the length of the hand is 56
mm
Solution
Here the distance travelled by the tip of the seconds hand of a clock in 1 minute is the circumference of
the circle and the length of the seconds hand is the radius of the circle. So,
r = 56 mm
Circumference
of the circle, C =2πr units
= 2×22/7×56
= 352mm
Therefore, distance travelled by the tip of the seconds hand of a clock in 1 minute is 352 mm.
Example5
The
radius of a tractor wheel is 77 cm. Calculate the distance covered by it in 35
rotations?
Solution
The
distance covered in one rotation = the circumference of the circle
= 2πr units
= 2×22/7×77
= 484cm
The
distance covered in one rotation = 484 cm
The
distance covered in 35 rotations =484 × 35 = 16940 cm
Example 6
A
farmer wants to fence his circular poultry farm with barbed wire whose radius
is 420 m. The cost of fencing is ₹12 per metre. He has ₹30,000 with
him. How much more amount will be needed to fence his farm?
Solution
The
radius of the poultry farm is = 420 m
The
length of the barbed wire for fencing the poultry farm is equal to the
circumference of the circle.
We
know that the circumference of the circle = 2 πr units
=
2×22/7×420 = 2640m
The
length of the barbed wire to fence the poultry farm = 2640 m
The
cost of fencing the poultry farm at the rate of ₹12 per metre = 2640 x 12
= ₹31,680
Given
that he has ₹30,000 with him.
The
excess amount required = ₹31,680 − ₹30,000 = ₹1,680.
Example 7
Kannan divides a circular disc of radius 14 cm
into four equal parts. What is the perimeter of a quadrant shaped disc?
Solution
To
find the perimeter of the quadrant disc, we need to find the circumference of
quadrant shape.
Given
that radius (r) = 14 cm.
We
know that the circumference of circle = 2 πr units
So,
the circumference of the quadrant arc = ![]()
![]()
![]()
Given,
the radius of the circle = 14 cm
Thus,
perimeter of required quadrant shaped disc = 14 + 14 + 22 = 50 cm.
4 Area of the Circle
Let us consider the following situation.
A bull is tied with a rope to a pole. The bull
goes round to eat grass. What will be the portion of grass that the bull can graze?
Can you tell what is needed to be found in the
above situation, Area or Perimeter? In this situation we need to find the area
of the circular region.
Let us find a way to calculate the area (A) of a
circle in terms of known area, that is the area of a
rectangle.
1.
Draw a circle on a sheet of paper.
2.
Fold it once along its diameter to obtain two
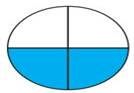
semicircles. Shade one half of the circle (below Fig)

3.
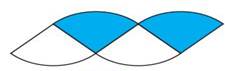
Again fold the semicircles to get 4 sectors. Below
Fig shows a circle divided into four sectors. The sectors are re-arranged and
made into a shape as shown in below Fig.
4.
Repeat this process of folding to eight folds,
then it looks like a small sectors as shown in the below Fig. The sectors are re-arranged
and made into a shape as shown in below Fig.
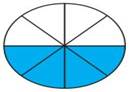
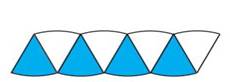
5.
Press and unfold the circle. It is then divided
into 16 equal sectors and then into 32 equal sectors. As the number of sectors
increase the assembled shape begins to look more or less like a rectangle, as
shown in below Fig.
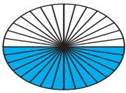

6.
The top and bottom of the rectangle is more or
less equivalent to the circumference of the circle. Hence the top of the
rectangle is half of the circumference = πr . The
height of the rectangle is nearly equivalent to the radius of the circle. When
the number of sectors is increased infinitely, the circle can be rearranged to
form a rectangle of length ‘πr ’ and breadth ‘r’.
We know that the area of the rectangle = l×b
=
πr×r
=
πr2
So, the area of the circle, A = πr2 sq units
Example 1
Find
the area of the circle of radius 21 cm (Use π = 3.14 )
Solution
Radius
(r) = 21 cm
Area
of a circle = πr2 sq units
=
3.14 × 21 × 21
=
1384.74
Area
of the circle = 1384.74 cm2
Example 2
Find the area of a hula loop whose diameter is
28 cm?
Solution
Given
the diameter (d) = 28 cm
Radius
(r) = 28/2 = 14
cm
Area
of a circle = πr2 sq units
=
22/7 × 14 × 14
=
616
So,
the area of the circle = 616 cm2
Example 3
The area of the circular region is 2464 cm2 . Find its radius and diameter.
Solution
Given
that the area of the circular region = 2464 cm2
πr2 = 2464
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Diameter
(d) = 2× r = 2×
28 = 56 cm.
Example 4
Find
the length of the rope by which a cow must be tethered in order that it may be
able to graze an area of 9856 sq.m
Solution
Given
that the area of the circule = 9856 cm2
πr2 = 9856
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore
the length of the rope should be 56 m.
5 Area of Pathways
We come across pathways in
different shapes. Here we restrict ourselves to two kinds of pathways namely
circular and rectangular.
5.1. Circular Pathways
We observe around us circular shapes
where we need to find the area of the pathway. The area of pathway is the
difference between the area of outer circle and inner circle. Let ‘R’ be the
radius of the outer circle and ‘r’ be the radius of inner circle.

Therefore, the area of the circular pathway = πR2 -
πr2
= π(R2 – r2)
sq. units.
5.2
Rectangular Pathways
Consider a rectangular park as
shown in Fig 2.23. A uniform path is to be laid outside the park. How do we
find the area of the path? The uniform path including the park is also a
rectangle. If we consider the path as outer rectangle, then the park will be
the inner rectangle.

Let l and b
be the length and breadth of the park. Area of the park (inner rectangle) = l b
sq.units. Let w be the width of the path. If L, B are
the length and breadth of the outer rectangle, then L = l + 2w and B = b + 2w .
Here, the area of the rectangular pathway = Area
of the outer rectangle – Area of the inner rectangle = (LB – lb) sq. units
Example 1
A
park is circular in shape. The central portion has playthings for kids
surrounded by a circular walking pathway. Find the walking area whose outer
radius is 10 m and inner radius is 3 m.
Solution
The
radius of the outer circle, R = 10 m
The
radius of the inner circle, r
= 3 m
The
area of the circular path =Area of outer circle −Area of inner circle
= πR2 - πr2
= π(R2 – r2)
sq. units.
![]()
![]()
![]()
Example 2
The radius of a circular flower garden is 21 m. A
circular path of 14 m wide is laid around the garden. Find the area of the
circular path.
Solution
The
radius of the inner circle r = 21m
The path is around the inner circle.
Therefore,
the radius of the outer circle, R =21 + 14 = 35 m
The area of the circular path =πR2 -
πr2
= π(R2 –
r2) sq. units.
![]()
![]()
![]() m2
m2
Example 3
The radius of a circular cricket ground is 76 m.
A drainage 2 m wide has to be constructed around the cricket ground for the
purpose of draining the rain water. Find the cost of constructing the drainage
at the rate of ₹180/- per sq.m.
Solution
The
radius of the inner circle (cricket ground), r = 76 m
A
drainage is constructed around the cricket ground.
Therefore,
the radius of the outer circle, R = 76 + 2 = 78
We
have, area of the circular path = π(R2 –
r2) sq. units.
![]()
![]()
![]() m2
m2
Given,
the cost of constructing the drainage per sq.m is ₹180.
Therefore,
the cost of constructing the drainage = 968 × 180 = ₹1,74,240.
Example 4
A
floor is 10 m long and 8 m wide. A carpet of size 7 m long and 5 m wide is laid
on the floor. Find the area of the floor that is not covered by the carpet.
Solution
Here,
L = 10 m
B
= 8 m
Area
of the floor = L × B = 10 × 8 = 80 m2
Area
of the carpet = l × b = 7 × 5 = 35 m2
Therefore,
the total area of the floor not covered by the carpet =80 – 35
=
45 m2