Number System
Introduction
Decimal Number
Fraction
which has denominator 10, 100, 1000 etc. are called Decimal Fractions.
A
decimal number is a number with a decimal point. Numbers left to the decimal
are 10 greater and number to the right of the decimal are 10 smaller.
Example:
Observe the following and write the fraction of the shaded portion and mention
in decimal form also-
1.
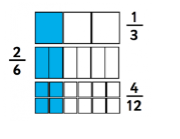
2.
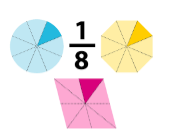
Example:
Represent the following fractions in decimal form by converting denominator
into ten or powers of 10-
|
S. no. |
Fraction |
Decimal
form |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
Now,
Consider the following situation. Ravi has planned to celebrate Pongal festival
in his native place Kanchipuram. He has purchased dress materials and groceries
for the celebration. The details are furnished below.
Bill 1 (ABC
Textiles)
|
S.no. |
Particulars |
Rate
(in Rs.) per m |
Length
of the material |
Price |
|
1. |
Pant
material |
120 |
4.75
m |
570
|
|
2. |
Shirt
material |
108 |
5.25
m |
567 |
|
3. |
Churidar
material |
150 |
4.50
m |
675 |
|
4. |
Saree
|
960
(per saree) |
5.50
m |
960 |
Bill 2
(Groceries)
|
S.
no |
Item |
Rate
(Rs.) |
Quantity
|
Price |
|
1 |
Rice
|
60/kg |
1.00
kg |
60 |
|
2 |
Dhal |
85/kg |
0.50
kg |
42.50 |
|
3 |
Jaggery |
40/kg |
1.75
kg |
70 |
|
4 |
Ghee |
420/kg |
0.25
kg |
105 |
|
5 |
Nuts |
800/kg |
0.10
kg |
80 |
|
6 |
Coconuts |
25 |
5 |
125 |
|
7 |
Banana |
60
/ dozen |
1
dozen |
60 |
|
8 |
Sugarcane |
50 |
2 |
100 |
|
|
|
Total |
|
642.50 |
What do
you observe in the bills shown above? The prices are usually represented in
decimals. But the quantities of length are represented in terms of metre and
centimetre and that of weight are represented in terms of kilograms and grams.
To express the quantities in terms of higher units, we use the concept of
decimals.
Representation
of decimal number:
The expanded form of 3768 is given by 3*1000 +
7*100 + 6*10 +8.
Representing the two numbers 3768 and 25.6 in
the place value grid, we get
|
|
th |
h |
t |
O |
Tenths |
|
3768 |
3 |
7 |
6 |
8 |
0 |
|
25.6 |
0 |
0 |
2 |
5 |
6 |
The decimal digits of a number have to be read
as separate digits.
Example:
Praveen goes trekking with his friends. He has to record the distance in
kilometres in his sports book. Can you help him? The trekking record for four
days are given below
(i)
4 m
(ii)
28 m
(iii)
537 m
(iv)
3983 m
Solution:
(i)
4 m = 4/1000 km = 0.004 km
(ii)
28 m = 28/1000 km = 0.028 km
(iii)
537 m = 537/1000 km = 0.537 km
(iv)
3983 m = 3983/1000 km = 3.983
km
Example: Express
the numbers given in expanded form in the place value grid. Also write its
decimal representation.
(i)
3*100+9*10+9*1+9* 
+5*
Solution: Representation
of the above number 399.95 is,
|
|
Hundred |
tens |
Ones |
Tenths |
Hundredths |
|
399.95 |
3 |
9 |
9 |
9 |
5 |
Problem based on above concept:
1. Express
the following in metres using decimals.
(i)
16 cm
(ii)
7 cm
2. Expand
the following decimal numbers. (i) 37.3 (ii) 658.37
3. Express
the following decimal numbers in place value grid and write the place value of
the underlined digit.
(i)
53.61
(ii)
263.271
4. A
cricket pitch is about 264 cm wide. It is equal to ____ m.
(i)
26.4
(ii)
2.64
(iii)
0.264
(iv)
0.0264
5. To
convert grams into kilograms, we have to divide it by
(i)
10000
(ii)
1000
(iii)
100
(iv)
10
Conversion
of fraction into decimal:
We are
familiar with fraction as a part of a whole. The place value of the decimal
digits of a number are tenths ( ),
hundredths ( ),
thousandths ( 
)
and so on. If the denominator of a fraction is any of 10, 102, 103,
… we can express them as decimals. Consider the example of distributing a box
of 10 pencils to ten students. The portion of pencils given to 6 students will
be 6/10 which can be expressed as 0.6.
If the
denominator of a fraction is any number that can be made as powers of 10 using
the concept of equivalent fractions, then it can also be expressed as decimals.
Consider the example of sharing 5 peanut cakes among five friends. The share of
one person is 1/5. To represent this fraction as a decimal number, we first
convert the denominator into 10. This can be done by writing the equivalent
fraction of 1/5, namely 2/10. Now the decimal representation of 2 10 is 0.2.
Conversion
of Decimals to Fractions:
As
we convert fractions into a decimal number, the decimal numbers can also be
expressed as fractions.
For
example, let the price of brand ‘x’ slippers be Rs. 399.95
Expanding
the above price, we get,
399.95 = 3*100+9*10+9*1+9* +5*
= 399+ ( 
)
= ( 
)
= ( 
).
Note: For any decimal number, number of zeroes in
the denominator and number of decimal digits are equal.
Example:
Write the fraction for each of the following:
(i)
6 hundreds + 3 tens + 3 ones +
6 hundredths + 3 thousandths.
Sol:
6*100+3*10+3*1+6*+3*
=633+
= 
(ii)
3 thousands + 3 hundreds + 4
tens + 9 ones + 6 tenths.
Sol:
3*1000+3*100+4*10+9*1+6*
= 3349+
=
.
Example:
Convert the following decimals into fractions.
(i)
0.0005
Sol: 
= 
(ii)
6.24
Sol:
=
.
Example: Write
the shaded portion of the figures given below as a fraction and as a decimal
number.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sol:
31
squares out of 56. Therefore, 31/56 =0.554.
Example:
Convert the following into simplest fractions.
(i)
0.04
Sol:
1/25
(ii)
3.46
Sol:
123/50
Example:
Express as a fraction of capsule contains 0.85 mg of medicine.
Sol:
0.85 = 0+8*+5* =
.
Comparison of Decimals:
We
follow these steps to compare decimals
Decimal
Numbers with Equal Decimal Digits
Step1:
Compare the whole number part of the two numbers. The decimal number that has
the greater whole number part is greater.
Step2: If the
whole number part is equal, then compare the digits at the tenths place. The
decimal number that has the larger tenths digit is greater.
Step3:
If the whole number part and the digits at the tenths place are equal, compare
the digits at the hundredths place. The decimal number that has the larger
hundredth digit is greater. The same procedure can be extended to any number of
decimal digits.
Decimal
Numbers with Unequal Decimal Digits
Let us
now compare the numbers 45.55 and 45.5. In this case, we first compare the
whole number part. We see that the whole number part for both the numbers are
equal. So, we now compare the tenths place. We find that for 45.55 and 45.5,
the tenth place is also equal. Now we proceed to compare hundredth place. The
hundredth place of 45.5 is 0 and that of 45.55 is 5. Comparing the hundredths
place, we get 0 < 5.
Therefore, 45.50 <
45.55.
Note: Zeros added to the right end of decimal
digits do not change the value of that decimal number.
Example: Velan
bought 8.36 kg of potato and Sekar bought 6.29 kg of potato. Which is heavier?
Solution:
Compare
8.36 and 6.29
Comparing
the whole number part, we get 8 > 6.
Therefore,
8.36 > 6.29.
Example: A
standard art paper is about 0.05 mm thick and matte coated paper is 0.09 mm
thick. Can you say which paper is thicker?
Solution:
Compare
0.05 and 0.09 by using the steps given above, the integral parts and tenths
places are equal. By comparing the hundredth place, we get 5 < 9.
Therefore,
0.05 < 0.09.
So
far, we discussed about the comparison of two decimal numbers. Extending this,
we can arrange the given decimal numbers in ascending or descending order.
Example: Now let
us arrange the long jump records of students in a school for 3 years in
ascending order
(i)
1 year -4.90 m
(ii)
2 year-4.91 m
(iii)
3 year-4.95 m
Solution:
The whole number parts of the
three decimal numbers are equal. The digits at tenths place are also equal. The
digits at hundredths place are 0, 1 and 5.
Here
0 < 1 < 5
Therefore,
the ascending order is 4.90, 4.91, 4.95.
Note: The descending order is 4.95,4.91, 4.90.
Note: 3.300 and 3.3 are the same.