SIMPLE INTEREST

Simple interest is a quick and easy method of calculating the interest charge on a loan. Simple interest is determined by multiplying the daily interest rate by the principal by the number of days that elapse between payments.

Simple Interest=P×I×N

P=principle

I=daily interest rate

N=number of days between payments

Converting Fractions to Percent:

Remember that a percent is really just a special way of expressing a fraction as a number out of 100100 .

To convert a fraction to a percent, first divide the numerator by the denominator. Then multiply the decimal by 100100 .

That is, the fraction 4848 can be converted to decimal by dividing 44 by 88 . It can be converted to percent by multiplying the decimal by 100100 .

4÷8=0.50.5×100

=504÷8

=0.50.5×100

=50

So, the fraction 4848 is equivalent to 50%

Example 1:

Write 2/25 as a percent.

Solution:

Since 2525 is larger than 22 , in order to divide, we must add a decimal point and some zeroes after the 22 . We may not know how many zeroes to add but it doesn't matter. If we add too many we can erase the extras; if we don't add enough, we can add more.

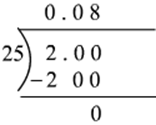
$https://www.varsitytutors.com/assets/vt-hotmath-legacy/hotmath_help/topics/converting-fractions-to-percent/conv_frac_to_perc_image01.gif$

So,

225=0.080.08×100=8225=0.080.08×100=8

Therefore, the fraction 225225 is equivalent to 8%8% .

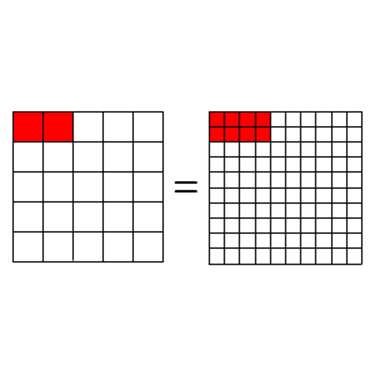
Look at the image below, it shows that the fraction 225225 is same as 88 out of 100100 , that is, 8%8% .

$https://www.varsitytutors.com/assets/vt-hotmath-legacy/hotmath_help/topics/converting-fractions-to-percent/image2.gif$

Example 2:

Write 7/4 as a percent.

Solution:

Divide 77 by 44 .

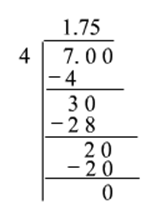
$https://www.varsitytutors.com/assets/vt-hotmath-legacy/hotmath_help/topics/converting-fractions-to-percent/conv_frac_to_perc_image02.gif$

So,

74=1.751.75×100=17574=1.751.75×100=175

Therefore, the fraction 7474 is equivalent to 175%175% .

Example 3:

Write 1/8 as a percent.
solution:

Divide 11 by .

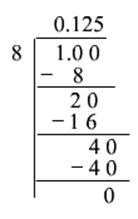
$https://www.varsitytutors.com/assets/vt-hotmath-legacy/hotmath_help/topics/converting-fractions-to-percent/conv_frac_to_perc_image3.gif$

So,

18=0.1250.125×100=12.518=0.1250.125×100=12.5

Therefore, the fraction 1818 is equivalent to 12.5%12.5% .

Converting percentage to a fraction:

The important fact to remember when dealing with percentages is that percent means 'out of 100'. To convert a percentage to a fraction, follow the steps below:

Step 1)

Change your percentage to a fraction by putting the percentage number over a denominator of 100.

Step 2)

Change it to simplest form if required.

You have now changed your percentage to a fraction

Example: Convert 11% to a fraction

Step 1:

Write down:

11/100

Step 2:

The percent is a whole number, go straight to step 3.

Step 3:

The fraction cannot be simplified further.

Answer = 11/100

Example: Convert 75% to a fraction

Step 1:

Write down:

75/100

Step 2:

The percent is a whole number, go straight to step 3.

Step 3:

Simplify the fraction (this took me two steps, you may be able to do it one!):

	÷5		÷ 5

75100	=	1520	=	34

	÷5		÷ 5

Answer = 34

Example: Convert 62.5% to a fraction

Step 1:

Write down:

62.5100

Step 2:

Multiply both top and bottom by 10 (because there is 1 digit after the decimal place)

	× 10

62.5100	=	6251000

	× 10

(See how this neatly makes the top a whole number?)

Step 3:

Simplify the fraction (this took me two steps, you may be able to do it one!) :

	÷ 25		÷ 5

6251000	=	2540	=	58

	÷ 25		÷ 5

Answer = 58

Converting From Percent to Decimal:

Percent means "per 100", so 50% means 50 per 100, or simply ⁵⁰/₁₀₀

When we divide 50 by 100 we get 0.5 (a decimal number).

So, to convert from percent to decimal:

divide by 100, and remove the "%" sign.

The Easy Way:

The easy way to divide by 100 is to move the decimal point 2 places to the left, so:

From Percent	To Decimal

move the decimal point 2 places to the left, and remove the "%" sign

Example: Convert 8.5% to decimal

Move the decimal point two places to the left: 8.5 → 0.85 → 0.085

(Note how we inserted an extra "0" as needed)

Answer 8.5% = 0.085

Example: Convert 250% to decimal

Move the decimal point two places to the left: 250. → 25. → 2.5

Answer 250% = 2.5

How to convert a given ratio into percentage?

We will follow the following steps for converting a ratio into a percentage:

Step I:

Obtain the ratio. Let the ratio be x : y

Step II:

Convert the given ratio into the fraction x/y.

Step III:

Multiply the fraction obtained in step II by 100 and put the percentage sign(%)

For example,

If the ratio is 12:4, convert it to the form 12/4, which is an equation we can solve. After that multiply the result by 100 to get the percentage.

12 ÷ 4 = 3
3 × 100 = 300%

TO CALCULATE THE PERCENTAGE INCREASE:

First: work out the difference (increase) between the two numbers you are comparing.

Increase = New Number - Original Number

Then: divide the increase by the original number and multiply the answer by 100.

% increase = Increase ÷ Original Number × 100.

è If your answer is a negative number then this is a percentage decrease.

TO CALCULATE PERCENTAGE DECREASE:

First: work out the difference (decrease) between the two numbers you are comparing.

Decrease = Original Number - New Number

Then: divide the decrease by the original number and multiply the answer by 100.

% Decrease = Decrease ÷ Original Number × 100.

è If your answer is a negative number then this is a percentage increase.

If you wish to calculate the percentage increase or decrease of several numbers then we recommend using the first formula. Positive values indicate a percentage increase whereas negative values indicate percentage decrease.

Examples - Percentage Increase and Decrease:

In January Dylan worked a total of 35 hours, in February he worked 45.5 hours – by what percentage did Dylan’s working hours increase in February?

Solution:

To tackle this problem first we calculate the difference in hours between the new and old numbers. 45.5 - 35 hours = 10.5 hours. We can see that Dylan worked 10.5 hours more in February than he did in January – this is his increase. To work out the increase as a percentage it is now necessary to divide the increase by the original (January) number:

10.5 ÷ 35 = 0.3 (See our division page for instruction and examples of division.)

Finally, to get the percentage we multiply the answer by 100. This simply means moving the decimal place two columns to the right.

0.3 × 100 = 30

Dylan therefore worked 30% more hours in February than he did in January.

In March Dylan worked 35 hours again – the same as he did in January (or 100% of his January hours). What is the percentage difference between Dylan’s February hours (45.5) and his March hours (35)? You may think that as there was a 30% increase between Dylan’s January hours (35) and February (45.5) hours that there will be a 30% decrease between his February and March hours. This assumption is incorrect – let’s calculate the difference.

First calculate the decrease in hours, that is: 45.5 - 35 = 10.5

Then divide the decrease by the original number (February hours) so:

è 10.5 ÷ 45.5 = 0.23 (to two decimal places).

Finally multiply 0.23 by 100 to give 23%. Dylan’s hours were 23% lower in March than in February.

Sometimes it is easier to show percentage decrease as a negative number – to do this follow the formula above to calculate percentage increase – your answer will be a negative number if there was a decrease. In Dylan’s case the decrease works out at -15.5. -10.5 ÷ 45.5 = -0.23. -0.23 × 100 = -23%.

Dylan's hours could be displayed in a data table as: