ALGEBRA
1 Introduction to Identities
In earlier classes, we have learnt to construct
algebraic expressions using exponential notations. For example, consider the
algebraic expression (a+b)2
= a2+2ab+b2 . Let us try to find the values of the
expression for the given values of a and b.
When a = 3 and b = 5,
L.H.S = ![]()
R.H.S![]()
Thus, for a =3 and b =5 ,
L.H.S = R.H.S
Similarly, when a = 4 and b = 7,
L.H.S = ![]()
R.H.S![]()
Also, for a = 4 and b =7 ,
L.H.S = R.H.S
Thus, we shall find that for any value of ‘a’
and ‘b’ L.H.S = R.H.S. Such an equality, which is true for every value of the
variable in it is called an identity. Thus, we observe that the equation (a+b)2 = a2+2ab+b2
is an identity.
In general, algebraic equalities which hold true
for all the values of the variables are called Identities.
2 Geometrical Approach to Multiplication of Monomials
We have already learnt that the operation of
multiplication can be modelled in different ways. The one that we use in this
unit is the representation of multiplication as a product table that is similar
to area.
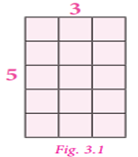
For example, the product 5![]() 3 can be represented as shown in Fig. 3.1,
which has five rows and three columns and it comprises 15 small squares. From
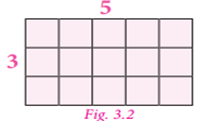
Fig. 3.2, it is also clear that the product of 5
3 can be represented as shown in Fig. 3.1,
which has five rows and three columns and it comprises 15 small squares. From
Fig. 3.2, it is also clear that the product of 5![]() 3 is
the same as the product of 3
3 is
the same as the product of 3![]() 5 [Since, multiplication is commutative].
5 [Since, multiplication is commutative].
Here, multiplication is represented using grid
model. The same can be represented using area model.
The area model helps us to understand
multiplication by decomposing the area of large rectangle into areas of smaller
rectangles. Also the same example which is discussed above may be decomposed as
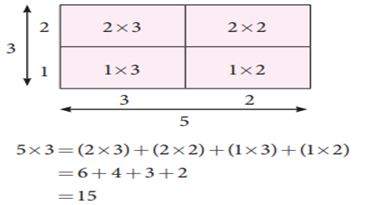
This decomposition model is very useful when we
are finding the product of large numbers.
3 Geometrical proof of Identities
By using this concept of multiplication of
monomials, let us try to prove the identities geometrically, which are very
much useful in solving algebraic problems.
3.1 Identity-1: ![]()
Consider four regions. One region is square
shaped with dimension 3![]() 3 (Grey).
Also, the other three regions are rectangle in shape with dimensions 4
3 (Grey).
Also, the other three regions are rectangle in shape with dimensions 4![]() 3 (yellow),
3
3 (yellow),
3![]() 2 (red) and 4
2 (red) and 4![]() 2 (Blue). Arrange these four regions to form a
rectangular shape as shown in the Fig. 3.8.
2 (Blue). Arrange these four regions to form a
rectangular shape as shown in the Fig. 3.8.
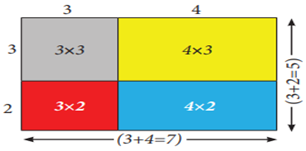
By
observing Fig. 3.8, we can note that,
Area of the bigger rectangle = Area of a square
(Grey ) + Area of Three rectangles
![]()
![]()
Where, LHS is
![]()
RHS is ![]()
Therefore, LHS = RHS.
In the similar way as explained above, let us
check for another set of four regions as shown in the Fig. 3.9.
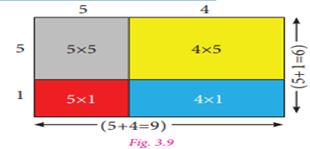
By observing Fig. 3.9, we can note that,
Area of the bigger rectangle = Area of a square
(Grey ) + Area of Three rectangles
![]()
![]()
![]()
![]()
Therefore, LHS = RHS.
Thus, equation (1) and (2) is true for given set
of any three values.
By generalising those three values as ‘x’, ‘a’
and ‘b’
we
get,![]()
That is, ![]()
Hence,![]() is an identity.
is an identity.
Now, let us prove this identity, geometrically.
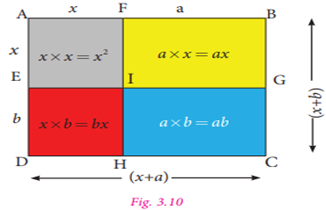
Let one side of a rectangle be (x +a) and the
other side be (x + b) units.
Then, the total area of the rectangle ![]()
From the Fig. 3.10, we can see that the
Area of the rectangle ABCD = area of the square AFIE + area
of the rectangle FBGI + area of the
rectangle EIHD + area
of the rectangle IGCH
![]()
![]()
From (3) and (4) we get,![]()
Hence, is![]() an identity.
an identity.
Example
1 Simplify the following using the identity ![]()
![]()
Solution
![]()
Let us represent the expression geometrically,
as shown in the Fig. 3.11.
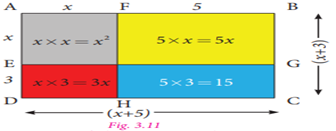
In the rectangle with length (x +5) and breadth
(x +3 ), we get,
Area of
bigger rectangle = Area of a square + Area of three rectangles
Therefore,
![]()
![]()
![]()
![]()
Let us represent the expression geometrically,
as shown in Fig. 3.12.
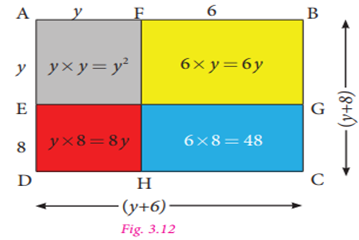
In the rectangle with length (y +6) and breadth (y +8) units, we get,
Area of bigger rectangle = Area of square + Area
of three rectangles
Therefore,
![]()
![]()
![]()
![]()
We
know the identity ![]()
Taking,
x = 40, a=3 and b= –4, we get
![]()
![]()
3.4 Identity-4: ![]()
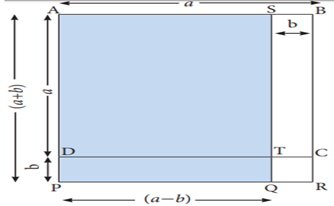
In the given figure, AB = AD = a.
So, area of square ABCD =a2.
Also, SB = DP = b.
Area of the rectangle SBCT = ab.
Similarly, area of the rectangle DPRC = ab.
Also, area of the square TQRC = b2.
Area of the rectangle DPQT = ab
– b2.
Now, AS = PQ = (a − b) and AP = SQ = (a +
b).
Hence, area of the rectangle APQS = area of square ABCD – area of rectangle
STCB
(the shaded rectangle) + area of rectangle DPQT
=
a2 –ab + (ab - b2)
=
a2 –ab + ab - b2
=
a2 – b2
Hence, (a + b) (a – b) = a2 – b2
Example
2 Simplify by using the identity (a + b) (a – b)
= a2 – b2
(i) (3x + 4)(3x − 4) (ii) 53 × 47.
Solution
(i)
![]()
Substitute,
a = 3x and b = 4 in the identity (a + b) (a – b) = a2 – b2,
we get,
![]()
![]()
![]()
(ii)
53 × 47 = (50 + 3) × (50
− 3).
Take, a = 50 and b = 3,
Substituting the values of ‘a’ and ‘b’ in the identity(a + b) (a – b) = a2 – b2, we
get
![]()
![]()
![]()
4 Factorisation using identities
A factor of a number is the number that exactly
divides a given number without leaving any remainder. For example, the factors
of 4 are 1, 2 and 4; the factors of 12 are 1, 2, 3, 4, 6 and 12. And, the
number can be expressed as product of its factors such as 12 = 1 × 12 or 2 × 6
or 3 × 4.
In the same way, algebraic expressions also have
factors that divide the expression exactly. Given an algebraic expression, the
factors of that algebraic expression are two or more expressions whose product
is the given expression. For example, ![]() hence the factors of the algebraic expression
hence the factors of the algebraic expression ![]() are x, x and y.
are x, x and y.
Example
3 Express the following algebraic expressions as
the product of its factors:
![]()
Solution
![]()
![]()
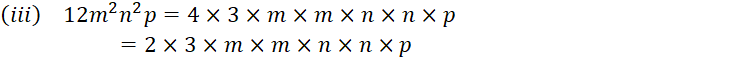
Example Factorise by
using the identity:![]()
![]()
Solution
![]()
![]()
![]()
![]()
Example
Factorise ![]()
Solution
![]()
![]()
This expression is in the form of identity ![]()
Hence, ![]()
![]()
Therefore, the factors of ![]()
5 Inequations
An algebraic statement
that shows two algebraic expressions being unequal is known as an algebraic inequation.
In general, when two
expressions are compared, one might be; less than (), greater than or equal to
(≥) the other.
In an inequation, the algebraic expressions are connected by one
out of the four signs of inequalities, namely, >, ≥, < and ≤.
5.1 Solving linear Inequations
A simple linear equation
has atmost one solution, but a linear inequation may have many solutions.
To solve an inequation, it is necessary to know the set of values that
the variable symbol can be substituted with. The collection of of all such values of an inequation
is known as solution of the inequation.
For example, the
solution of the equation 3x − 3 = 12 is 5. (How?) Let us find the
solution for the inequation 3x − 3 < 12,
where x is a natural number. Note that, the solutions of this inequation are ‘natural numbers’. Now,
Add 3 on both sides, we
get 3x − 3 + 3 < 12 + 3 ⇒
3x < 15
Divide by 3 on both
sides, we get ![]()
Hence, x takes value which is less than 5 and x
is a natural number. Thus, the solution for this inequation
are 1, 2, 3 and 4.
Note:
When ‘x’ is not restricted to a natural number, the solution
includes all values less than 5.
Rules
to solve inequation
While solving an inequation,
the rules for transposition in case of inequalities are the same as for
equations.
1.
Addition
of the same number on both sides of the inequation
does not change the value of the inequation. Example:
10 > 5 ⇒
10 + 1 > 5 + 1 ⇒
11 > 6.
Extending this result, when
adding any number ‘x’ instead of 1, the inequality 10 + x > x + 5 remains
unchanged.
2.
Subtraction
of the same number from both sides of the inequation
does not change the value of the inequation. Example:
10 > 5 ⇒
10 − 1 >
5 − 1 ⇒
9 > 4.
Extending this result, when
subtracting any number x instead of 1, the inequatity
10− x > x − 5remains unchanged.
3.
Multiplication
by the same positive number on both sides of the inequation
does not change the value of the inequation. Example:
10 > 5 ⇒
10 × 2 >
5 × 2 ⇒
20 > 10.
Similarly, when multiplying any
positive number x instead of 2, the inequatity 10 × x
> x × 5 remains unchanged.
4.
Division
by the same non-zero positive number on both sides of the inequation
does not change the value of the inequation
Example
Solve:
2x + 4 < 18, where x is a natural number.
Solution
2x + 4 < 18
2x + 4 – 4 < 18
− 4 [Subtracting 4 from both sides]
2x < 14 [Divide by 2
on both sides]
x
< 7
Since the solution
belongs to natural numbers, that are less than 7, we take the values of the x
as 1, 2, 3, 4, 5 and 6.
Therefore, the solutions
are 1, 2, 3, 4, 5 and 6.
Example
Solve: 5 − 7x ≥ 33, where x is an
integer.
Solution
![]()
![]()
![]()
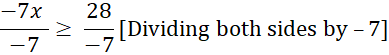
x
≤−4 [since, it is divided by a negative number, the inequality is
reversed]
Since, solution belongs
to the set of integers, that are less than −4, we take the values of x as
–4, –5, –6, ...
Therefore, the solutions
are –4, –5, –6,... .
5.2 Graphical representation of Inequation
The solutions of an inequation can be represented on the number line by marking
the true values of solutions with different colour on the number line.
Look into the following inequations and its graphical representation on number
line. Here, we consider the solution belongs to natural numbers. That is, each
and every value of the solution is a natural number.
1.
When x < 3, the solution in
natural numbers are 1 and 2. Its graph on number line is shown below:

2.
When x ≥ 3, the solutions
are natural numbers 3, 4, 5, ... and its graph is as shown below:
![]()
3.
To mark the values represented
by the inequation 2 ≤ x ≤ 5, the
solutions are set of natural numbers 2, 3, 4 and 5 and its graph is as given
below:
![]()
Example
Represent the solutions −8 < 2x <
10 in a number line, where x is a natural number.
Solution
![]()

![]()
Since the solution
belongs to the set of natural numbers, the solutions are 1, 2, 3 and 4.
It’s
graph on the number line is shown below:

Example
Solve the inequation: −2 ≤ z + 3 ≤ 5, where z is an
integer. Also, represent the solution, graphically.
Solution
![]()
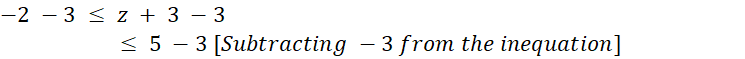
![]()
Since the solution
belongs to integers, the solutions are –5, –4 , –3,
–2, –1, 0, 1 and 2.
It’s
graph on the number line is shown below:
