GEOMETRY

Types of symmetry

i. Line of Symmetry

Look at the Fig. 4.1 given on the below.

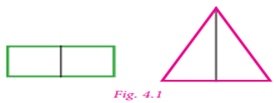
In each figure a line divides the figure into two identical halves. Such figures are symmetrical about the line. The line that divides any figure into two equal halves such that each half exactly coincides with the other is known as the line of symmetry or axis of symmetry.

A figure may have one, two, three or more lines of symmetry. Some figures which has lines of symmetry are shown in Fig. below

ii. Reflectional symmetry

When an object is seen in a mirror, the image obtained on the other side of the mirror is called its reflection.

An object and its mirror image are perfectly identical to each other. The left and right sides of an object appear inverted in the mirror. The object and its reflection image show mirror symmetry. The mirror line here is the line of symmetry. Mirror symmetry is called reflectional symmetry.

The following shapes are examples of reflectional symmetry.

iii. Rotational Symmetry

An object is said to have a rotational symmetry if it looks the same after being rotated about its centre through an angle less than 360°.

When an object rotates around a fixed axis if its appearance of size and shape does not change then the object is supposed to be rotationally symmetrical.

Rotational symmetry can be observed in the following Fig

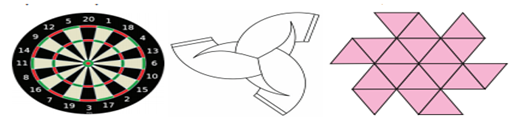
The minimum angle of rotation of a figure to get exactly the same figure as original is called the angle of rotation.

The total number of times a figure coincides with itself in one complete rotation is called the order of rotational symmetry. We can only rotate the figure up to 360 degrees.

iv. Translational Symmetry

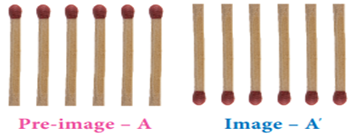
An image has translational Symmetry if it can be divided by straight lines into a sequence of identical figures. Translational symmetry results from moving a figure to a certain distance in a certain direction.

Thus, translation symmetry occurs when a pattern slides to a new position. The sliding movement involves neither rotation nor reflection.

1.Introduction

Symmetry is a fundamental part of geometry, nature, and shapes. It creates patterns that help us to recognize the beauty of the nature. An object exhibits symmetry if it looks the same after a transformation, such as reflection or rotation.

Rotation, translation, reflection concepts within geometrical transformations are used in daily life, architectural designs, art and technology. Above all an aesthetic sense of beauty is observed in objects due to symmetry. Let us see the three types of transformation namely translation, reflection and rotation in this chapter.

2.Symmetry through transformations

Transformation describe how geometric figures of the same shape are related to one another. Figures or shapes in a plane can be translated, reflected or rotated to get new figures.

The original figure is called the pre-image and the new figure is called the image. Pre-images are denoted by A, B, C … etc., and the images are denoted by A', B', C', … etc. A' can be read as A prime.

The operation that maps or moves the pre-image onto the image is called the transformation.

A transformation is a specific set of rules that change the pre-image onto the image.

In this chapter we are going to learn three types of transformation.

2.1. Translation:

A translation is a transformation that moves all points of a figure in the same distance in the same direction.

From these examples we can observe that all points of a figure move in the same distance and in the same direction.

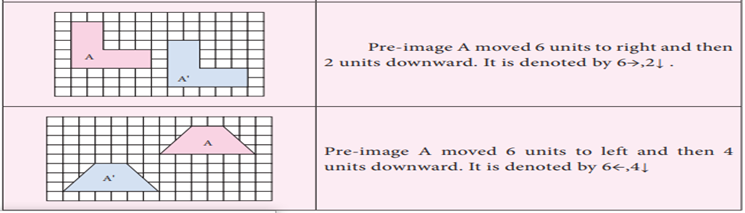
Using a grid paper, we can specify a translation by how far the shape is moved horizontally and then vertically.

In horizontal, the right side movement is denoted by → and the left side movement is denoted ←.

In vertical, the upside movement is denoted ↑ and the downward movement is denoted ↓.

Example 1 Find the new position of each point using the translation given.

(i). 4 → 2 ↓ (ii). 6 ← 5 ↓ (iii). 6 → 4 ↑ (iv). 4 ← 4 ↓

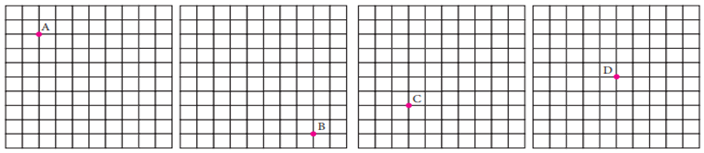
Solution

2.2. Reflection

A reflection is a transformation that “flips” or “reflects” a figure about a line.

After a figure is reflected, it looks like a mirror image of itself. The line that a figure is flipped over is called a line of reflection.

Observe the following pictures.

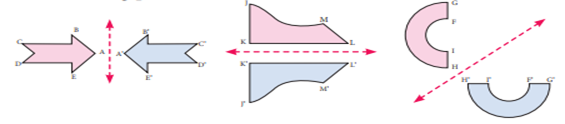
In the above pictures (Fig), the figures are reflected by a line. This line is called a line of reflection. Here the red line is the line of reflection.

We can observe that the figures and its reflections are exactly the same distance from the line of reflection on both sides. The line of reflection may be horizontal or vertical or slanting and also it may be on the shape or outside the shape.

How to reflect a shape about a line?

To reflect the shape about the line of reflection, we have to reflect every vertex individually and then connect them again.

First, choose one of the vertices and draw the line through this vertex so that it is perpendicular to the line of reflection.

Now measure the distance from the vertex to the line of the reflection, and mark a point that has the same distance on the other side. It can be done by using either a ruler or a compass. Repeat the process for all the other vertices of the shape.

Finally connect all the reflected vertices in the correct order to get the reflection of the shape.

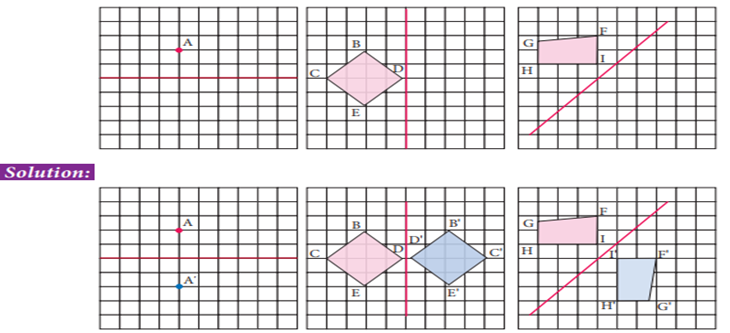
Example 2 Reflect the shape in each of the following pictures with given line of reflection.

2.3. Rotation

A rotation is a transformation that turns every point of the pre-image through a specified angle and direction about a point.

The fixed point is called the centre of rotation. The angle is called the angle of rotation. A rotation is also called a turn.

The default direction of a rotation is the anti-clockwise direction. The angle of rotation can be any value between 0 and 360 degrees, both are included.

Rotation of 360° is called a full turn, rotation of 180° is called a half turn, rotation of 90° is called a quarter turn.

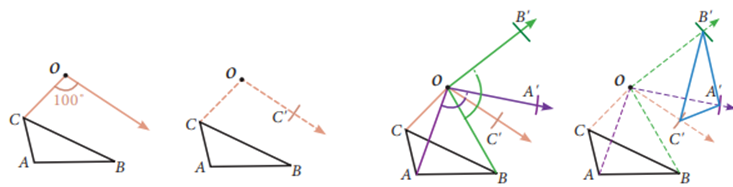
To rotate a shape about a point with the given angle, we have to rotate every vertex individually and connect them again. Here ΔABC is rotated about O with angle of 100°.

Step1. Draw CO. Make angle of 100° with vertex C and side CO using a protractor.

Step2. Use a compass to construct CO’ = CO

Step3. Locate A’ and B’ in the similar way.

Step4. Join A’, B’, C’ to form ΔA’B’C’

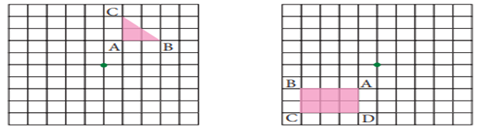
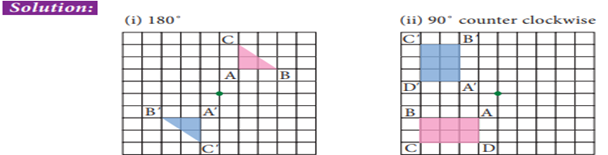
Example 3 Rotate the pink shape about the green point by given angle of rotation and direction

(i) 180˚ (ii) 90˚ counter clockwise

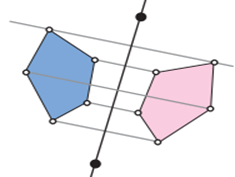
Example 4 Describe the transformation involved in the following pair of figures. Write translation, reflection or rotation.

Solution:

(i) Reflection (ii) Rotation (iii) Translation

3 Construction of circles and concentric circles

3.1 circles

The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle.

The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle. The word radius is used in two senses – in the sense of a line segment which joins the centre of the circle and a point on the circle and in the sense of length of the line segment.

A circle groups all points in the plane on which it lies into three categories. They are:

(i) the points which are inside the circle, which is also called the interior of the circle;

(ii) the points on the circle and

(iii) the points outside the circle, which is also called the exterior of the circle.

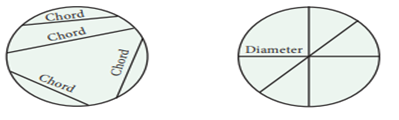
If two points on a circle are joined by a line segment, then the line segment is called a chord of the circle.The chord, which passes through the centre of the circle, is called a diameter of the circle.

3.2 Construction of circles

Now let us learn to construct circle with given radius and diameter.

Example Construct a circle of radius 5 cm with centre O.

Step 1: Mark a point O on the paper. 5cm

Step 2: Extend the compass distance equal to the radius 5 cm O A

Step 3: At center O, Hold the compass firmly and place

the pointed end of the compass.

Step 4: Slowly rotate the compass around to get the circle.

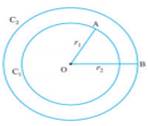
3.3 The Concentric Circles

Circles drawn in a plane with a common centre and different radii are called concentric circles .

The area between the two concentric circles is known as circular ring.

Width of the circular ring (see below Fig.) = OB – OA= r₂ – r₁.

3.4 Construction of Concentric Circles

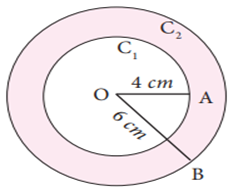
Example Draw concentric circles with radii 4 cm and 6 cm and shade the circular ring. Find its width.

Step 1: Draw a rough diagram and mark the given measurements.

Step 2: Take any point O and mark it as the centre.

Step 3: With O as centre and draw a circle of radius OA = 4 cm

Step 4: With O as centre and draw a circle of radius OB = 6 cm.

Thus the concentric circles C₁ and C₂ are drawn.

Width of the circular ring = OB – OA = 6 – 4 = 2 cm.

Summary

Ø A transformation is a specific set of rules that change the preimage onto the image.

Ø A translation is a transformation that moves all points of a figure in the same distance in the same direction.

Ø In horizontal, the right-side movement is denoted by → and the left side movement is denoted by ←.

Ø In vertical, the upside movement is denoted by ↑ and the downward movement is denoted by ↓.

Ø A reflection is a transformation that “flips” or “reflects” a figure about a line.

Ø A rotation is a transformation that turns every point of the pre-image through a specified angle and direction about a point. The fixed point is called the centre of rotation. The angle is called the angle of rotation.

Ø A rotation is also called a turn.

Ø The default direction of a rotation is the anti-clockwise direction.

Ø Rotation of 360° is called a full turn, rotation of 180° is called a half turn, rotation of 90° is called a quarter turn.

Ø The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle. The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle.

Ø If two points on a circle are joined by a line segment, then the line segment is called a chord of the circle.

Ø The chord, which passes through the centre of the circle, is called a diameter of the circle.

Ø Circles drawn in a plane with a common centre and different radii are called concentric circles.

Ø The area between the two concentric circles is known as circular ring

Ø Width of the circular ring(w) = r₂ – r₁