STATISTICS
1.Collection of data
We need to collect data
having the specific information in our mind. Suppose the specific information
needed by us is to know the height of class VII students, then we should
collect specific data related to their heights and ages rather than the data
related to health record of students.
The purpose for which a
data is to be collected has to be kept in mind before starting the process of
data collection. Then only we can get the desired information, which is appropriate
to the purpose. Let us look into a few situations that are given below.
Data can be generated in
many situations around us. For example,
Ø The
number of trees planted in your locality.
Ø The
highest temperatures recorded in all the major cities of India during the year
2018.
Ø The
least amount of rainfall recorded in all the districts of Tamil Nadu during the
year 2018.
2.Organisation of Data
We first collect data,
record it and organise them. To understand this, consider an example which
deals with the weights of 10 students . The data is
given below.
Ø Anbu-20
kg; Nambi-19 kg; Nanthitha- 20 kg; Arul- 24 kg;
Ø Mari-25
kg; Mathu-22 kg; Pavithra – 23 kg; Beeman- 26 kg;
Ø Arthi-21
kg; Kumanan-25 kg.
Let us try to answer the
following questions.
(i)
Who is the least weight of all?
(ii)
How many students weigh between
22 kg to 24 kg?
(iii)
Who is the heaviest of all?
The data mentioned above
is not easy to understand.
If the data is arranged
according to the order of weights, it will be easy for answering the questions.
Observe the following table.
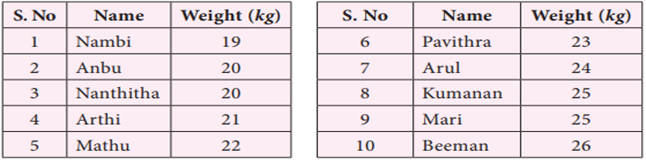
Now we can answer the
above questions easily. Hence it is essential to organise the data to obtain
any kind of inferences from the data. Organisation of data is helpful to
understand quickly and get an overall view of data.
3.Representative values
We have come across situtations where we use the term ‘average’ in our
day-to-day life. Consider the following statements.
Ø The
average temperature at Chennai in the month of May is 40° c.
Ø The
average marks in mathematics unit test of class is 74.
Ø Mala’s average
study time is 4 hours.
Ø Mathan’s average
pocket money per week is ` 100.
40° c is the
representative temperature of Chennai in the month of May which does not mean
that everyday temperature is 40° c in the month of May. Since the average lies
between the highest and the lowest value of the given data, we say average is a
measure of central tendency of the group of data. Different forms of data need
different forms of representative or central value to describe it. We study
three types of central values of data namely Arithmetic Mean, Mode and Median
in this chapter.
4.Arithmetic Mean
Consider this situation.
Mani and Ravi started
collecting shells in the sea shore with an agreement to share the shells
equally after collection. Finally, Mani collected 50 shells and Ravi collected
30 shells. Now, if both of them share equally, find the number of shells each
one gets?
We find it using
arithmetic mean or average. To find the average, add the numbers and divide by
2. Hence,
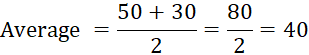
Average lies between 30
and 50.
Hence, each of them will
get 40.
Thus to find the
arithmetic mean (average), we have to add all the observations and divide the
sum of all observations by the number of observations.

Example
1 The daily wages of a worker for 10 days is as
follows. Find the average income of the
worker.

Solution

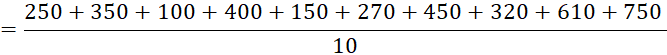
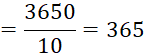
Hence,
the average income of the worker is 365.
Example 2 If the mean of the following numbers is 38,
find the value of x.
48, x, 37,
38, 36, 27, 35, 34, 38, 49, 33.
Solution

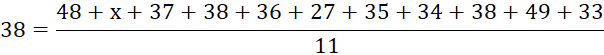
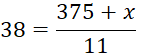
![]()
![]()
![]()
![]()
Hence, the value of x is
43.
5.Mode
Consider the example of
sale details of different sizes of footwear in a shop for a week.

The shopkeeper has to
replenish his stock at the end of the week. Suppose we find the arithmetic mean
of the footwear sold,
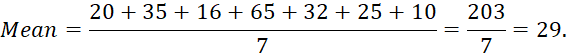
Average number of
footwear is 29. This means that the shopkeeper has to get 29 pairs of footwear
in each size. Will it be wise to decide like this?
It has to be observed
that the maximum purchase falls on the footwear of size 8 inches. So the
shopkeeper has to get more number of footwear of size 8 inches. Hence
arithmetic mean does not suit for this purpose. Here we need another type of
representative value of data called ‘Mode’.
Mode is the value of the data which occurs maximum number of
times.
Consider another
example.
A shopkeeper analyses
his sales data of readymade shirts to plan for the stock according to the
demand. The sale details of shirts are given below.

Here he observes that
there is a equal demand for shirts of sizes 30"
and 34" . Now this data has two modes as there are
two maximum occurrences namely 30" and 34" .
He stocks more shirts of these 2 sizes. Note that, this data has two mode and
it is known as bimodal data.
Example 3 Find the mode of the given set of numbers.
5, 7, 10, 12,
4, 5, 3, 10, 3, 4, 5, 7, 9, 10, 5, 12, 16, 20, 5
Solution
Arranging the numbers in
ascending order without leaving any value, we get,
3, 3, 4, 4, 5, 5, 5, 5,
5, 7, 7, 9, 10, 10, 10, 12, 12, 16, 20
Mode of this data is 5,
because it occurs more number of times than the other values.
Example
4 The marks obtained by 11 students of a class in
a test are 23, 2, 15, 38, 21, 19, 23, 23, 26, 34, 23. Find
the mode of the marks.
Solution
Arranging the given
marks in ascending order, we get,
2, 15, 19, 21, 23, 23,
23, 23, 26, 34, 38.
Clearly, 23 occurs
maximum number of times. Hence mode of marks=23.
Example
5 Find the mode of the following data 123, 132,
145, 176, 180, 120
Solution
From the above data, we
can see that there is no repetition of values in the given data. Each
observation occurs only once, so there is no mode.
5.1 Mode of large data
When size of the data is
large, it is not easy to identify the value which occurs maximum number of
times. In that case, we can group the data by using tally marks and then find the
mode.
Consider the example to
find the mode of the number of goals scored by a football team in 25 matches.
The goal scored are 1, 3, 2, 5, 4, 6, 2, 2, 2, 4, 6, 4, 3, 2, 1, 1, 4, 5, 3, 2,
2, 4, 3, 0, 1.
To find the mode of this
data, the number of goals score starting from 0 and ending with a maximum of 6
is represented in the form of a table.
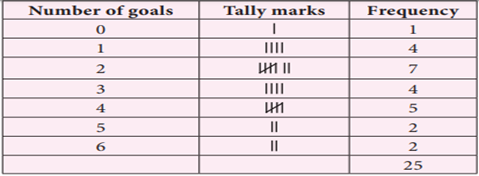
From the table we
observe that the highest frequency is 7, which corresponds to number of goals,
that is 2. Hence, the mode is 2.
Example 6 Find the mode of the following data.
14, 15, 12, 14, 16, 15, 17, 13, 16, 16,
15, 12, 16, 15, 13, 14, 15, 13, 15, 17, 15, 14,
18, 19, 12, 14, 15, 16, 15, 16, 13,
12.
Solution
We tabulate the data as
follows.
The whole data ranges
from 12 to 19.
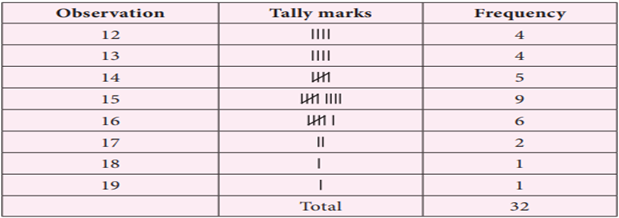
The highest frequency is
9 which corresponds to the value 15.
Hence the mode of this
data is 15.
6 Median
Let us consider the
following situation.
Rajam
an old student of the school wanted to provide financial support to a group of
15 students, who are selected for track events. She wanted to support them on
the basis of their family income. The monthly income of those 15 families are
given below.
₹3300, ₹5000,
₹4000,
₹4200,
₹3500,
₹4500,
₹3200,
₹3200,
₹4100,
₹4000,
₹4300,
₹3000,
₹3200,
₹4500,
₹4100.
Rajam
would like to give them an amount to their family.
If we find the mean, we
get
Arithmetic mean, A.M =![]()
Can
the amount of ` 3873.3 be given to all of them irrespective of their salary? Is
` 3873.3 is the suitable representative here? No, this is not suitable here
because a student with family income ` 3000 and a student with family income `
5000 will receive the same amount. Because the representative measure used here
is not sutable for the above data, let us find the
mode for this data.

Here mode is 3200 which
means there are more number of students with a family income of 3200. But this does not suite our
purpose. Hence, mode is also not suitable. Is there any other representative
measures that can be used here? Yes.
Let us look at another
representative value which divides the data into two halves exactly. First, let
us arrange the data in ascending order.
That is, 3000, 3200,
3200, 3200, 3300, 3500, 4000, 4000, 4100, 4100, 4200, 4300, 4500, 4500, 5000.
After arranging the
income in ascending order, Rajam finds 8th value
(4000) which divides the data into two halves. It helps her to decide the
amount of financial support that can be given to each of the students. Note
that 4000 is the middle most value.
This kind of representative value which is obtained by
choosing the middle item is known as Median.
Thus in a given data,
arranged in ascending or descending order, the median gives us the middle
value.
Consider another
example, where the data contains even number of terms 13, 14, 15, 16, 17 and
18. How to find the middle term for this example? Here the number of terms is 6, that is an even number. So we get, two middle terms
namely 3rd and 4th term. Then, we take the average of the two terms (3rd and
4th term) and the value we get is the median.
That is, Median ![]()
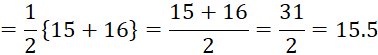
Here, to find median we
arrange the values of the given data either in ascending or descending order,
then find the average of the two middle values.
So we conclude that, to
find median,
(i)
arrange
the data in ascending or descending order.
(ii)
If the number of terms (n) is
odd, then 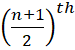 term
is the median.
term
is the median.
(iii)
If the number of terms (n) is
even, then average of 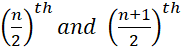 terms
is the median.
terms
is the median.
Example
7 Find the median of the following golf scores.
68, 79, 78, 65, 75, 70, 73.
Solution
Arranging the golf
scores in ascending order, we have,
65, 68, 70, 73, 75, 78,
79
Here n = 7 , which is odd.
Therefore, Median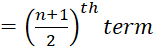
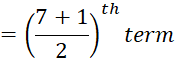
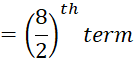
![]()
Hence, the Median is 73.
Example 8 The weights
of 10 students (in kg) are 35, 42, 40, 38, 25, 32, 29, 45, 20, 24
Find the median of their weight?
Solution
Arranging the weights in
ascending order, we have,
20, 24, 25, 29, 32, 35,
38, 40, 42, 45
Here, n = 10 , which is even.
Therefore, median weight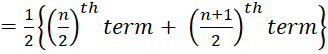
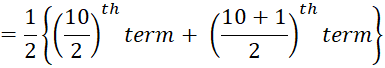
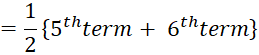
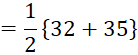
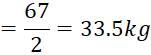
Hence, Median is 33.5
kg.
Example
9 Create a collection of 12 observations with
median 16.
Solution
As the number of
observations is even, there are two middle values.
The average of those
values must be 16.
We will now find any
pair of numbers whose average is 16. Say 14 and 18.
Now an example of data
with median 16 can be 2, 4, 7, 9, 12, 14, 18, 24, 28, 30, 45, 62.
Summary
Ø Based
on the purpose, appropriate data has to be collected and organised to find the
representative of data.
Ø Representative
of data are also known as measures of central tendency.
Ø Arithmetic
mean is the most commonly used representative of data and is calculated by the
formula.
§ ![]()
Ø Mode
is the value of the data which occurs maximum number of times.
Ø A
data may have more than one mode as well as no mode.
Ø A
data is of large size, mode can be found out after grouping.
Ø Median
is the middle most value of the given data.
Ø To
find the median for the given data,
(i) arrange the
data in ascending or descending order.
(ii)If the
number of terms (n) is odd, then 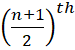 term
is the median.
term
is the median.
(iii)
If the number of terms (n) is
even, then average of 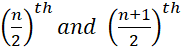 terms
is the median.
terms
is the median.