Algebra

Introduction:

The word algebra comes from the title of the Arabic book Ilm al-jabrwa’l-mukabala by the Persian mathematician and astronomer al-Khwarizmi. Algebra is the study of mathematical symbols and rules for calculating these symbols. In arithmetic, only numbers and their arithmetical operations (such as +,-, ×, ÷) occur. In algebra, numbers are often represented by symbols called variables.

Polynomial:

A special kind of algebraic expression is a polynomial. In a polynomial all variables are raised to only whole number powers.

Example:

x+y+z, 4x²+3x+7, mn etc.

Monomial:

An expression which contains only one term is called a monomial.

Example:

4x, 3x²y, -2y²

Binomial:

An expression which contains only two terms is called a binomial.

Example:

2x+3, 5y²+9y, a² b²+2b

Trinomial:

An expression which contains only three terms is called a trinomial.

Example:

2a²b-8ab+b², m²-n²+3

Polynomial:

An expression which contains more than three terms is called a polynomial.

Example:

x² + (a+b) x+ab+5, a³+b³+c³+abc

Difference between an Algebraic Expression and a Polynomial:

Algebraic Expression may contain whole numbers, fractions, and negative powers on their variables.

Example:

4x^3/2-3x+9, 2y²+ (5/y)-3, 3x²-4x+1

Polynomial contains only whole numbers as the power of their variables.

Example:

4x²-3x+9, 2y⁶+5y³-3

Multiplication of Algebraic Expressions:

² Multiply the signs of the terms. That is, the product of two like signs are positive and the product of two unlike signs are negative.

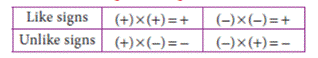
² Multiply the corresponding co-efficient of the terms.

² Multiply the variable factors by using laws of exponents.

If 'x' is a variable and m, n are positive integers then,

x^m × xⁿ = x^m+n

Example:

x³ × x⁴ = x³⁺⁴= x⁷

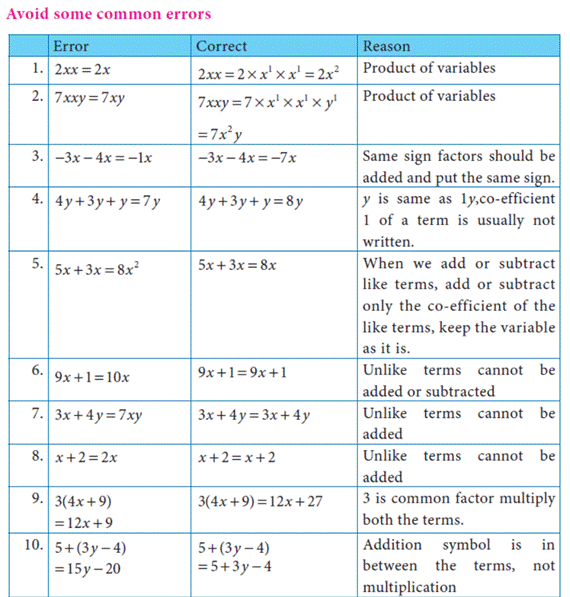
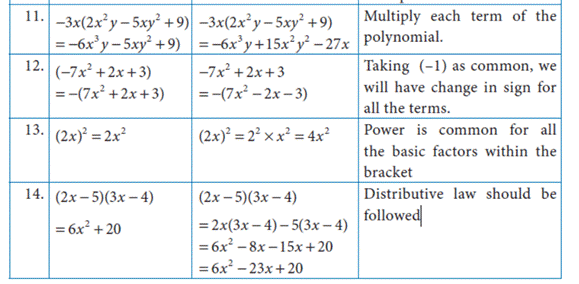
NOTE:

Product of two terms is represented by the symbols ( ), dot (.) or ×

Example 3.1:

If the side of a square carpet is 3x² metre, then find its area.

Solution:

The area of the square carpet, A = (side x side) sq. units.

= 3x² × 3x²

= 3 × 3 × x² × x²

A = 9x⁴ sq.m

Example 3.2:

If the length and breadth of a rectangular painting are 4xy³ and 3x²y. Find its area.

Solution:

Area of the rectangular painting, A = (l x b) sq. units

= (4xy³) (3x²y)

= (4 × 3) (x × x²) (y³ × y)

A = 12x³y⁴

Example 3.3:

Find the product of 3x²and (-4x)

Solution:

(3x²) × (-4x) = (+) (-) (3 × 4) (x² × x)

=-12x³

Example 3.4:

Find the product of 2x²y², 3y²z and -z²x³

Solution:

(2x²y²) × (3y²z) × (-z²x³) = (+) × (+) × (-) × (2×3×1) (x² × x³) (y²× y²) (z× z²)

= -6x⁵y⁴z³

Multiplication of a Polynomial by a Monomial:

Distributive law:

If a is a constant, x and y are variables then a(x + y) = ax+ay

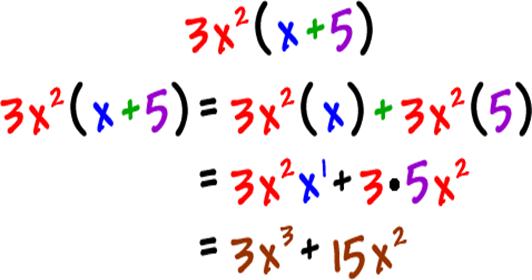
Example 3.5:

Multiply (3xy+7) by (-4y)

Solution:

-4y (3xy+7) = -4y (3xy) + (-4y) (7)

= (-4 × 3) x × y × y + (-4 × 7) y

= -12xy²-28y

Example 3.6:

Multiply 3x²y and (2x³y³ -5x²y+9xy)

Solution:

3x²y (2x³y³ -5x²y+9xy) = 3x²y (2x³y³)-3x²y (5x²y) +3x²y (9xy)

Multiplying each term of the polynomial by the monomial

= (3×2) (x² × x³) (y × y³)-(3 × 5) (x² × x²) (y × y) + (3× 9) (x² × x) (y×y)

= 6x⁵y⁴-15x⁴y²+27x³y²

Example 3.7:

If Guru wants to multiply the expressions (2x + 3y + 50) and 3xy, what is the resultant expression?

Solution:

The resultant expression = 3xy × (2x + 3y + 50)

=3xy (2x) + 3xy (3y) +3xy (50)

=6x²y+9xy²+150xy

Example 3.8:

Ram deposited 'x' number of Rs.2000 notes, 'y' number of Rs.500 notes, 'z' number of Rs. 100 notes in a bank and Velan deposited '3xy' times of amount of what Ram had deposited. How much amount did Velan deposit in the bank?

Solution:

Amount deposited by Ram = (x × 2000+ y × 500 + z × 100)

= Rs. (2000x+500y+100z)

Amount deposited by Velan = 3xy times x Amount deposited by Ram

= 3xy x (2000x + 500y+ 100z)

= (3×2000) (x×x×y) + (3×500) (x×y×y) + (3×100) (x×y×z)

= Rs. (6000x²y+1500xy²+300xyz)

Multiplication of Two Binomials:

Example 3.9:

Multiply (2x+5y) and (3x-4y)

Solution:

(2x+5y) × (3x-4y) = 2x (3x-4y) + 5y (3x-4y)

= 6x²-8xy+15xy-20y²

= 6x²+7xy-20y² (simplify the like terms)

Division of Algebraic Expressions:

Division is the reverse operation of multiplication.

There are four ways of division on algebraic expressions.

They are division of

• Monomial by a Monomial

• Polynomial by a Monomial

• Polynomial by a Binomial

• Polynomial by a Polynomial

Division of a Monomial by another Monomial:

Example 3.10:

Velu pastes ' 4xy' pictures in one page of his scrap book. How many pages will he need to paste 100x²y³ pictures? (x, y are positive integers)

Solution:

Total number of pictures = 100x²y³

Each page contains = 4xy pictures

= 100x²y³ /4xy

= 25x^2-1y^3-1

= 25xy² pages

Division of an Algebraic Expression (Polynomial) By a Monomial:

To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.

Example 3.11:

Divide (5y³-25y²+8y) by 5y

Solution:

(5y³-25y²+8y) ÷ 5y = (5y³-25y²+8y) / 5y

= (5y³/5y) - (25y²/5y) + (8y/5y)

= y^3-1 - 5y^2-1+ (8/5)

= y²-5y + (8/5)

Example 3.12:

Sethu travelled (4x² +3xy² + 5x) km in '2x' hrs. Find his speed of travel.

Solution:

Speed = distance travelled / time taken

= (4x² +3xy² + 5x) / 2x

= (4x²/2x) + (3xy²/2x) + (5x/2x)

= 2x^2-1+ (3/2 y²) + (5/2)

Speed = (2x + (3/2 y²) + (5/2) km/ hr.

Example 3.13:

Divide (10m²-5m) by (2m-1)

Solution:

(10m²-5m) / (2m-1) = [5m (2m-1)] / (2m-1)

(Taking common factor from the numerator)

= 5m

Identities:

An identity is an equation satisfied by any value that replaces its variable(s). Some of the basic identities are the following:

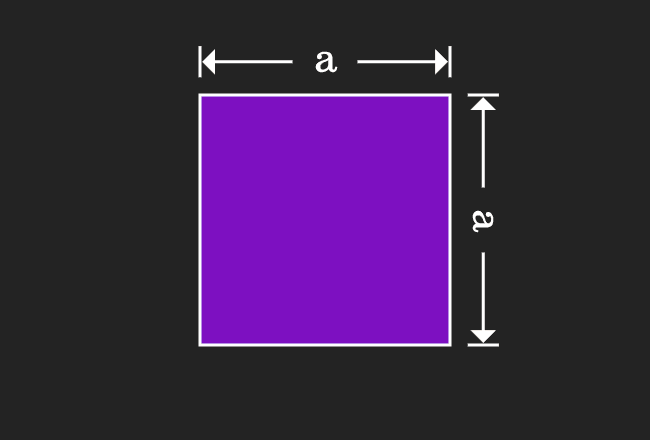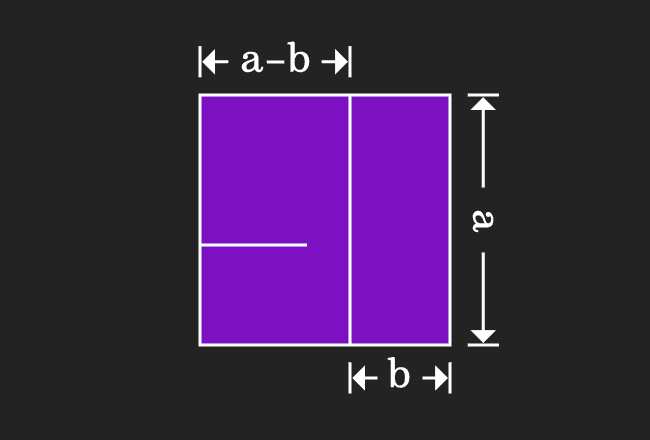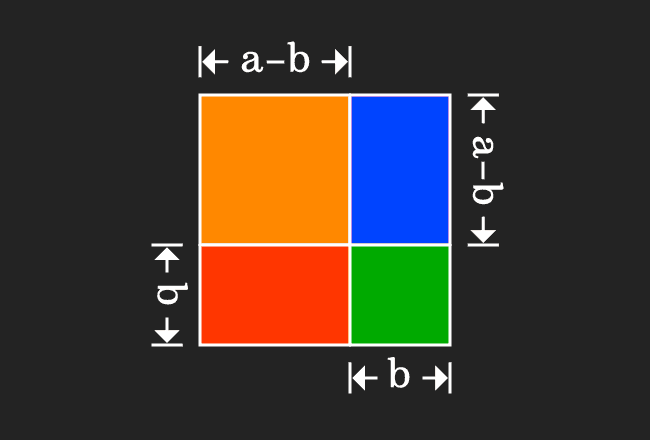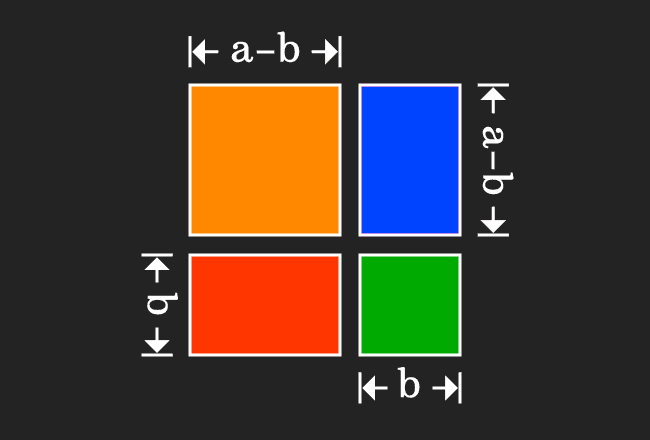
(a+b)² = a²+b²+2ab,

(a-b)² = a²+b²-2ab,

(a² - b²) = (a+b) (a-b),

(x+a)(x+b) = x²+ (a+b)x+ab

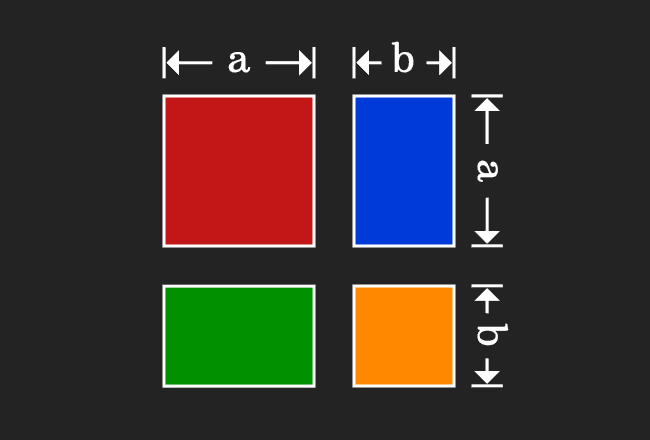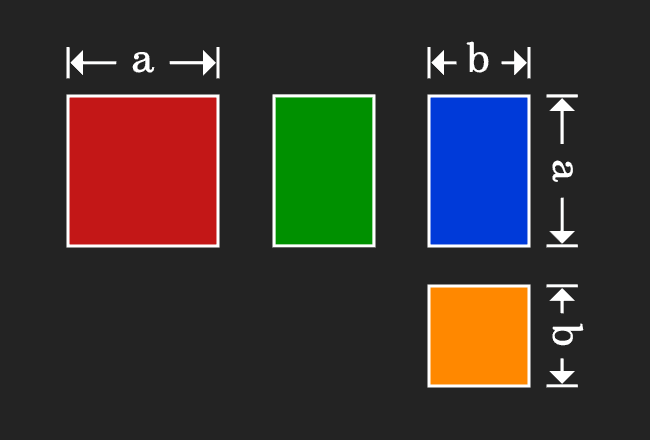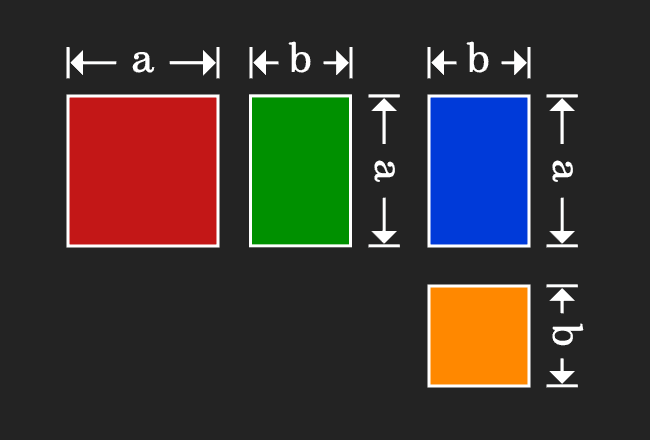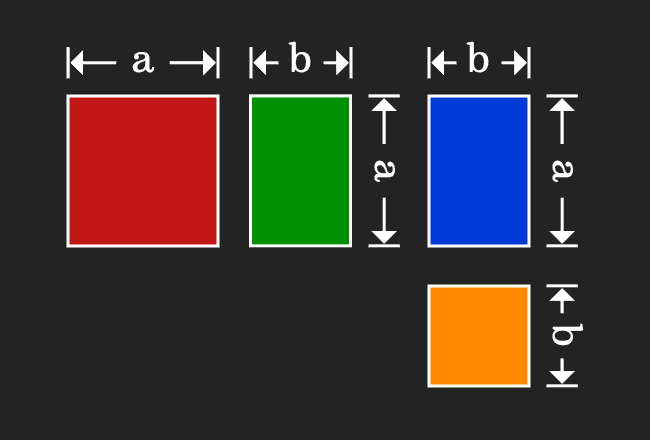
Applications of Identities:

Example 3.14:

Find the value of (3a+4c)² by using (a+b)²

Solution:

Here a = 3a and b = 4c

(a+b)² = a²+b²+2ab

(3a+4c)² = (3a)² + 2(3a) (4c) + (4c)²

= 3²a² + (2×3×4) (a×c) + 4²c²

(3a+4c)² = 9a²+24ac+16c²

Example 3.15:

Find the value of 998² using (a-b)² identity.

Solution:

998 = 1000-2

(998)² = (1000-2)²

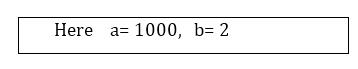
(a-b)² = a²+b²-2ab

(1000-2)² = (1000)² -2(1000) (2) +2²

= 1000000-4000+4

=996004

Example 3.16:

Simplify (3x+5y) (3x-5y) by using (a+b) (a-b) identity.

Solution:

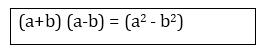
Here a= 3x, b= 5y

(3x+5y) (3x-5y) = (3x)² - (5y)²

= 3²x²-5²y²

= 9x²-25y²

Example 3.18:

Simplify (5x+3) (5x+4) by using (x+a) (x+b) identity.

Solution:

(x+a) (x+b) = x² + (a+b) x+ab

Here x= 5x and a=3, b=4

(5x+3)(5x+4) = (5x)² + (3+4) (5x)+(3) (4)

= 5²x² + (7) (5x) + 12

=25x²+35x+12

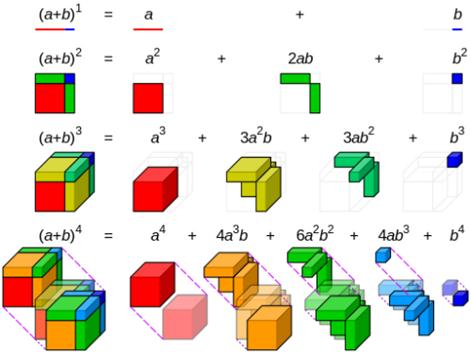
Cubic Identities:

Geometrical Interpretation:

Here In the left hand side, there is a cube whose Side is (a + b) then its volume is equal to, sum of a cube whose side is 'a' units, 3 cuboids whose sides are (a, a and b) units, 3 more cuboids whose sides are (a, b, b) units and a cube whose is 'b' units.

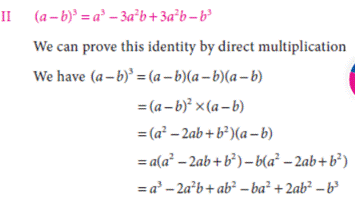
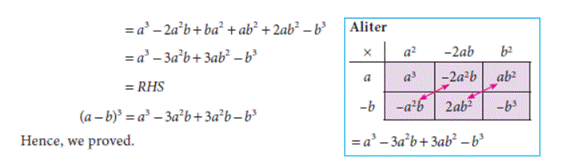
Geometrical interpretation:

Let us take a cube whose side is 'a' units, make one more cube whose side is 'b' units (b < a) at one of its corners. Complete the diagram with respect to sides to get cubes and cuboids in it.

Hence the volume of the cube of side (a - b) is obtained by removing 4 elements namely 3 cuboids whose sides are (a, a and b) units and cube of side 'b' units from the cube whose side is 'a' units and finally 3 cuboids of sides (a, b and b) units are added to get the cube whose side is (a - b)

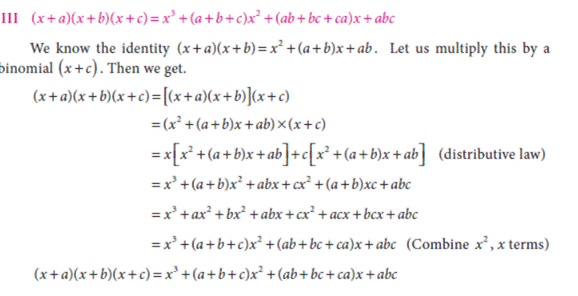
Geometrical interpretation:

The geometrical illustration of the above identity is the cuboid whose

Length, breadth, and height are (x+a), (x+b), (x+c) and whose volume is (I x b x h) that is v=(x+a) (x+b) (x+c). This cuboid contains a cube of side 'x' units , 3 cuboids of sides (a,b,x),(b,c,x) and (c,a,x)and and one cuboid of side (a,b,c)

Easier ways of deducting the above cubic identities:

Applications of Cubic Identities:

Example 3.19:

Expand (x+4)³

Solution:

Here a=x, b=4

(a+b)³ = a³+3a²b+3ab²+b³

(x+4)³ = (x)³+3(x)²(4) + 3(x) (4)²+(4)³

= x³+3x²(4) +3(x) (16) + 64

= x³+12x²+48x+64

Example 3.20:

Find the value of (103)³

Solution:

(103)³ = (100+3)³

Here a=100 , b=3

(a+b)³ = a³+3a²b+3ab²+b³

(100+3)³ = (100)³+3(100)²(3) + 3(100) (3)²+ (3)³

= 1000000+3(10000) (3) + 3(100) (9) + 27

= 1092727

Example 3.21:

Expand (y-5)³

Solution:

Here a=y, b=5

(a-b)³ = a³-3a²b+3ab²-b³

(y-5)³ = (y)³-3(y)²(5) +3(y) (5)²-(5)³

= y³+3y²(5)+3y(25)-125

= y³+15y²+75y-125

Example 3.22:

Find the value of (98)³

Solution:

(98)³ = (100-2)³

Here a=100, b=2

(a-b)³=a³-3a²b+3ab²-b³

(100-2)³ = (100)³-3(100)²(2) + 3(100) (2)²-(2)³

=1000000-3(10000) (2) + 3(100) (4)-8

= 1000000-60000+1200-8

= 941192

Example 3.23:

Expand (x+3) (x+5) (x+2)

Solution:

Here a=3, b=5, c=2

(x+a)(x+b)(x+c) = x³ + c(a+b+c) x + (ab+bc+ca)

(x+3)(x+5)(x+2) = (x)³ + (3+5+2)x+((3)(5)+(5)(2)+(2)(3))

= x³+10x²+(15+10+6)x+30

= x³+10x²+31x+30

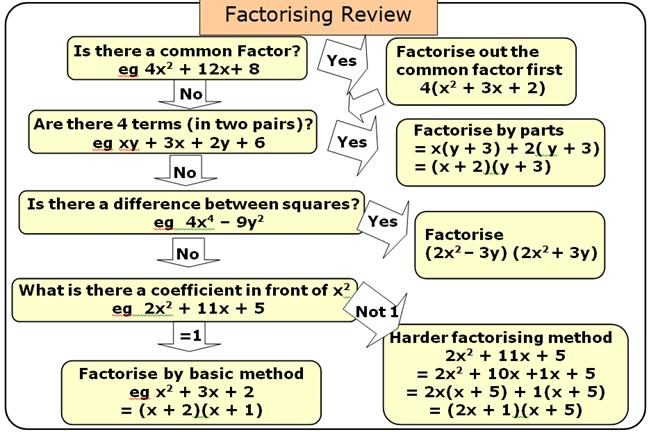
Factorisation:

Expressing an algebraic expression as a product of two or more expressions is called the factorisation.

Note that ‘1’ is a factor for all numbers and expressions.

So, when we factorise the expressions, follow the suitable type of factorisation given below to get two or more factors other than 1. Stop doing the factorisation process once you have taken out all the common factors from the expression and then list out the factors.

Type: 1 Factorisation by taking out the common factor from each term.

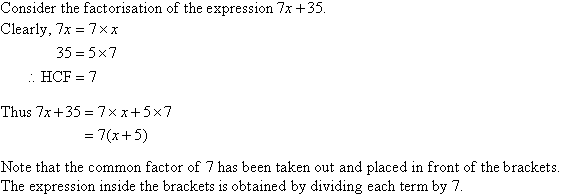
Example 3.24:

Factorise: 2m³ —5m² + 9m

Solution:

Taking out the common factor ‘m’ from each term, we get

2m³ —5m² + 9m = m (2m² —5m + 9)

Example 3.25:

Factorise 4x²y+8xy

Solution:

4x²y+8xy = (2×2×x×x×y) + (2×2×2×x×y)

Taking out the common factor 2, 2, x. y, we get

4x²y+8xy = 2×2×x×y(x+2)

= 4xy(x+2)

Type: 2 Factorisation by taking out the common binomial factor from each term

Example 3.26:

Factorise: (2x+5) (x-y) + (4y) (x-y)

Solution:

Taking out the common binomial factor (x-y), we get,

(2x+5)(x-y) + (4y)(x-y) = (x-y)(2x+5+4y)

Type: 3 Factorisation by grouping

Sometimes, the terms of a given expression are grouped suitably in such a way that they have a common factor so that the factorisation is easy to take out common factor from those terms.

Example 3.27:

Factorise: x²+yz+xy+xz

Solution:

x²+yz+xy+xz = (x²+xy) + (yz+xz)

= x(x+y) + z(y+x)

= x(x+y) + z(x+y) (since addition is commutative)

Taking out the common factor (x+y), we get

x²+yz+xy+xz = (x+y) [x+z]

Type: 4 Factorisation using identities

Example 3.28:

Factorise x²+8x+16

Solution:

x²+8x+16 = x²+8x+4²

(x²)+2(x) (4) + (4)² = (x+4)²

x²+8x+16 = (x+4)²

Example 3.29:

Factorise 49x²-84xy+36y²

Solution:

49x²-84xy+36y² = 7²x²-2(7x) (6y) + 6²y²

= (7x)²-2(7x) (6y)+(6y)²

(a-b)² = a²+b²-2ab

Here a=7x, b=6y

(7x)²-2(7x) (6y)+(6y)² = (7x-6y)²

49x²-84xy+36y² = (7x-6y)²

Example 3.30:

Factorise 49x²-64y²

Solution:

49x²-64y² = (7x)²-(8y)²

a²-b² = (a+b) (a-b)

Here a=7x, b=8y

(7x)²-(8y)² = (7x+8y) (7x-8y)

49x²-64y² = (7x+8y) (7x-8y)

Type: 5 Factorisation of the expression (ax²+bx+c)

Example 3.31:

Factorise x²+8x+15

Solution:

Here a=1, b=8, c=15

The product =a×c=1×15=15

The sum =b =8

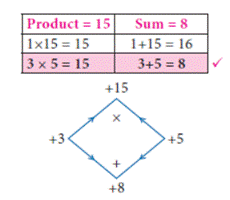
x²+8x+15 = (x²+3x) + (5x+15) (since the middle term 8x can be written as 3x+5x)

= x(x+3) + 5(x+3) (taking out the common factor x+3)

= (x+3) (x+5)

Factorisation Of Cubic Identities:

The factorisable forms of the cubic identities are

a³+b³ = (a+b) (a^2-ab+b²)

a³-b³ = (a-b) (a²+ab+b²)

Example 3.34:

Factorise 8p³+q³

Solution:

8p³+q³ = (2p)³+q³

a³+b³ = (a+b) (a^2-ab+b²)

Here a=2p, b=q

(2p)³+q³ = (2p+q) ((2p)²-(2p) (q) + (q)²)

8p³+q³ = (2p+q) (4p²-2pq+q²)

Example 3.35:

Factorise 81x³-3y³

Solution:

81x³-3y³ = 3(27x³-y³)

= 3[(3x)³-y³]

a³-b³ = (a-b) (a²+ab+b²)

Here a=3x, b=y

3[(3x)³-y³] = 3{(3x-y) [(3x)² + (3x) (y)+y²]}

81x³-3y³ = 3{(3x-y) [(3x)² + (3x) (y)+y²]}