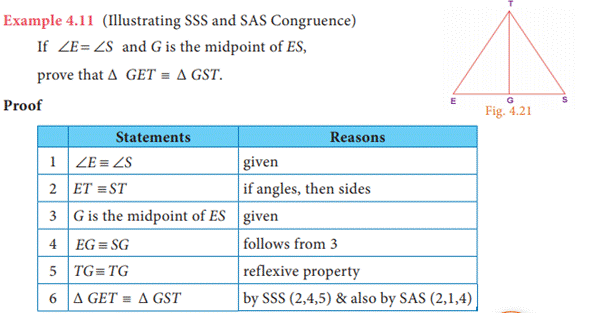
Geometry

4.1 Introduction

Geometry, as we all know studies shapes by looking at the properties and relations of points, circles, triangles of two dimensions and solids.

4.2 Similar Triangles

Similar figures mathematically have the same shape but different sizes. Two geometrical figures are said to be similar (~) if the measures of one to the corresponding measures of the other are in a constant ratio. In other words, every part of a photographic enlargement is similar to the corresponding part of the original.

Some examples where similar triangles are seen and used in real life are :

(i) To determine the distances between light and the target in the light beams, the height of any building, objects, people etc., by analyzing the shadows and using the scale modelling.

(ii) To analyse the stability of bridges.

(iii) In designing the work by the architects.

Similarity Properties:

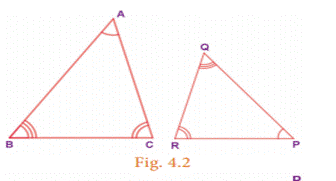
1. Two triangles are similar if two angles of one triangle are equal respectively to two angles of the other triangle. In the Fig. 4.2, ∠A=∠P , ∠B= ∠Q Therefore, ∆ ABC ~ ∆ PQR. This is, AA Similarity. This is also called as AAA Similarity.

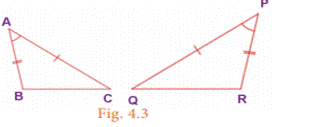
2. Two triangles are similar if two sides of one triangle are proportional to two sides of the other triangle and the included angles are equalAC/PQ = AB/PR ∠A= ∠P and hence ∆ ACB ~ ∆ PQR. This is SAS Similarity.

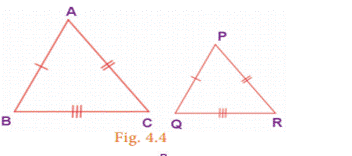
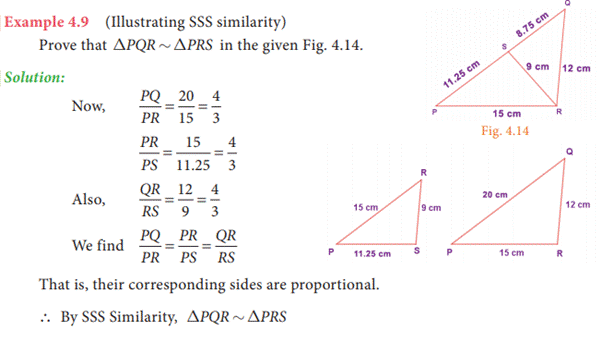
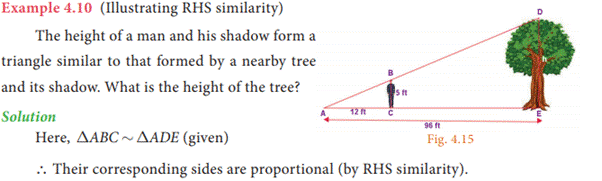
3. Two triangles are similar if their corresponding sides are in the same ratio. That is, if AB/PQ = AC/PR = BC/QR, then ∆ ABC ~ ∆ PQR. This is SSS Similarity.

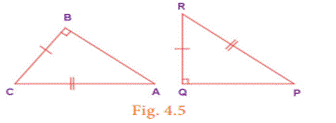
4. Two right triangles are similar if the hypotenuse and a leg of one triangle are respectively proportional to the hypotenuse and a leg of the other triangle. This is RHS Similarity.

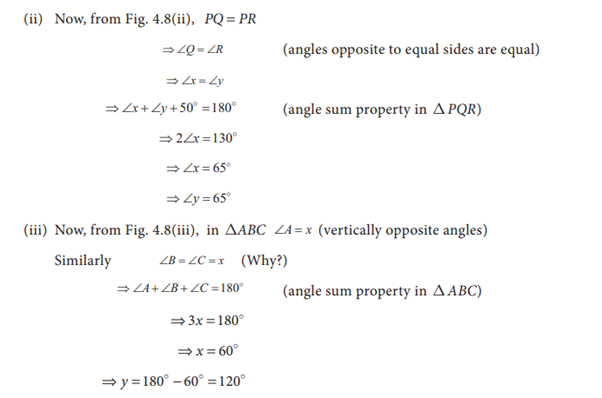
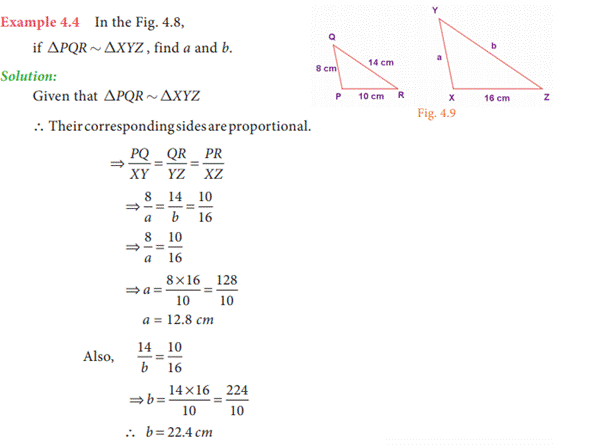
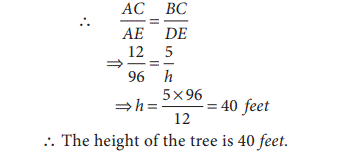
4.3 Congruent Triangles

Congruent figures are exactly the same in shape and size. In other words, shapes are congruent if one fits exactly over the other.

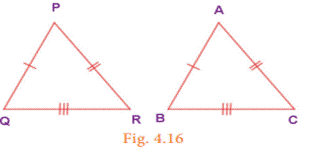
Here, two given triangles PQR and ABC are congruent (|||) because PQ=AB, QR=BC and PR=AC. Both triangles match exactly one on the other. This is denoted as PQR ≡ ABC

Some examples where congruent triangles are seen and used in real life are:

(i) In the construction of structures like railway bridges to make them strong and stable against strong winds and when under load.

(ii) In buildings where it can protect from the sun by reflecting off opposite triangular faces.

(iii) Used in kite making by the children and also in the playground equipment Geodesic dome.

There are 4 ways by which one can prove that two triangles are congruent. They are:

(i) SSS (Side – Side – Side)

(ii) SAS (Side – Angle – Side)

(iii) ASA (Angle – Side –Angle)

(iv) RHS (Right Angle–Hypotenuse– Side)

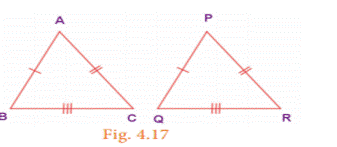
(i) SSS (Side – Side – Side) Congruence

If the three sides of a triangle are congruent to the three sides of another triangle, then the triangles are congruent.That is AB=PQ, BC=QR and AC = PR

⇒ ∆ ABC ≡ ∆ PQR.

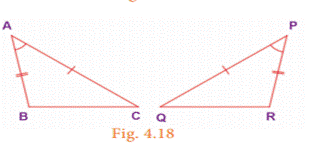
(ii) SAS (Side – Angle – Side) Congruence

If two sides and the included angle (the angle between them) of a triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. Here, AC=PQ, ∠A=∠P and AB=PR and hence

∆ACB ≡ ∆ PQR.

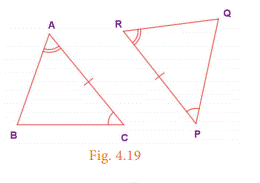
(iii) ASA (Angle-Side-Angle) Congruence

If two angles and the included side of a triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent. Here, ∠A=∠R, CA=PR and ∠C = ∠P and hence ∆ABC ≡ ∆RQP

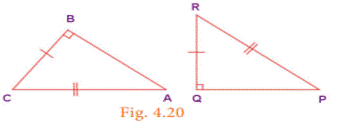
(iv) RHS (Right Angle – Hypotenuse – Side)

If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent. Here, BC = QR, AB = PQ and AC = PR and hence ∆ ABC ≡ ∆ PQR.

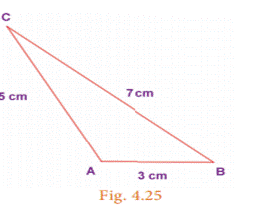
4.4 Construction of Quadrilaterals

➢ We have already learnt how to draw triangles in the earlier classes. A polygon that has got 3 sides is a triangle. To draw a triangle, we need 3 independent measures. Also, there is only one way to construct a triangle, given its 3 sides.

For example, to construct a triangle with sides 3cm, 5cm and 7cm, there is only one way to do it.

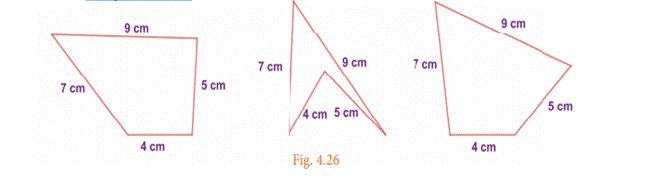
➢ A polygon that is formed by 4 sides is called a quadrilateral. But, a quadrilateral can be of different shapes. They need not look like the same for the given 4 measures.

For example, some of the quadrilaterals having their sides as 4 cm, 5 cm, 7 cm and 9 cm are given below.

So, to construct a particular quadrilateral, we need a 5th measure. That can be its diagonal or an angle measure. Moreover, even if 2 or 3 sides are given, using the measures of the diagonals and angles, we can construct quadrilaterals.

4.4.1 Constructing a quadrilateral when its 4 sides and a diagonal are given

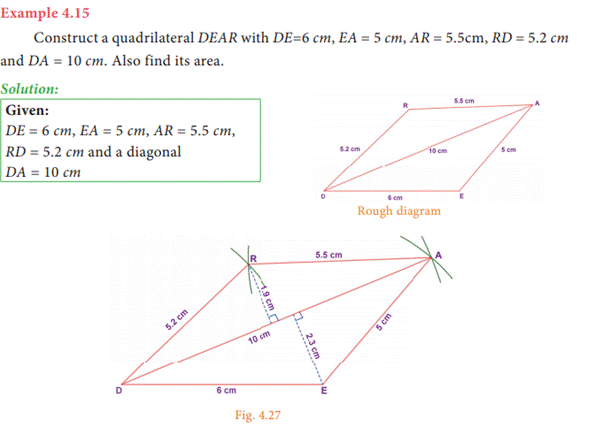
Steps:

1. Draw a line segment DE = 6 cm.

2. With D and E as centers, draw arcs of radii 10 cm and 5 cm respectively and let them cut at A.

3. Join DA and EA.

4. With D and A as centres, draw arcs of radii 5.2 cm and 5.5 cm respectively and let them cut at R.

5. Join DR and AR

6. DEAR is the required quadrilateral.

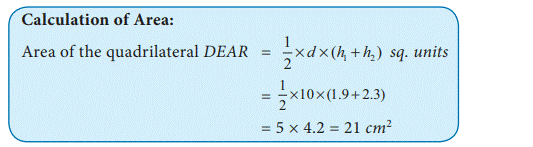
4.4.2 Construct a quadrilateral when its 3 sides and 2 diagonals are given

Steps:

1. Draw a line segment NI = 4.5 cm.

2. With N and I as centres, draw arcs of radii 5.5 cm and 4.3 cm respectively and let them cut at C.

3. Join NC and IC.

4. With N and I as centres, draw arcs of radii 3.5 cm and 5 cm respectively and let them cut at E.

5. Join NE, IE and CE.

6. NICE is the required quadrilateral

4.4.3 Construct a quadrilateral when its 4 sides and one angle are given

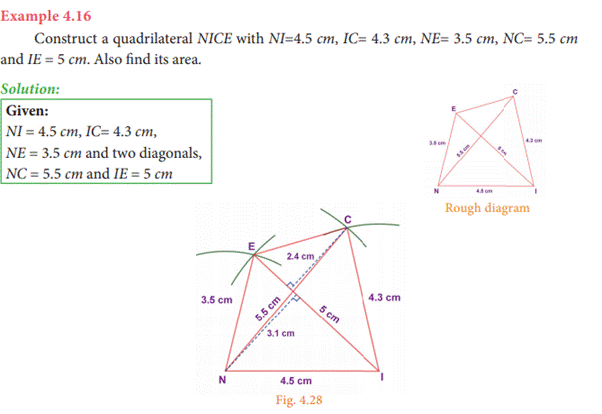
Steps:

1. Draw a line segment MA = 4 cm.

2. Make ∠ = A 85°.

3. With A as center, draw an arc of radius 3.6 cm. Let it cut the ray AX at T.

4. With M and T as centres, draw arcs of radii 5 cm and 4.5 cm respectively and let them cut at H.

5. Join MH and TH.

6. MATH is the required quadrilateral

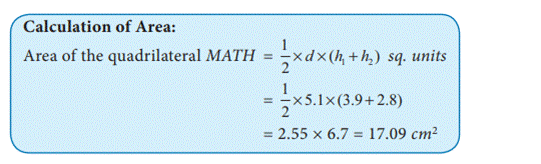
4.4.4 Construct a quadrilateral when its 3 sides and 2 angles are given

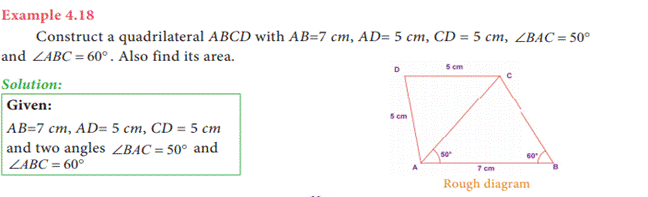
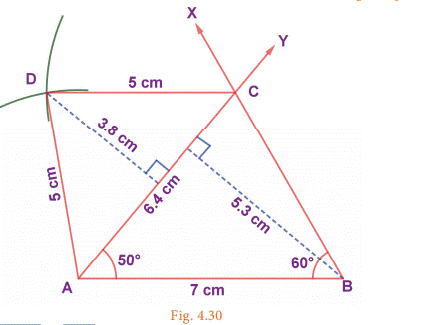
Steps:

1. Draw a line segment AB = 7 cm.

2. At A on AB, make ∠ = BAY 50° and at B on AB, make ∠ = ABX 60° . Let them intersect at C.

3. With A and C as centres, draw arcs of radius 5 cm. each. Let them intersect at D.

4. Join AD and CD.

5. ABCD is the required quadrilateral

4.4.5 Construct a quadrilateral when its 2 sides and 3 angles are given

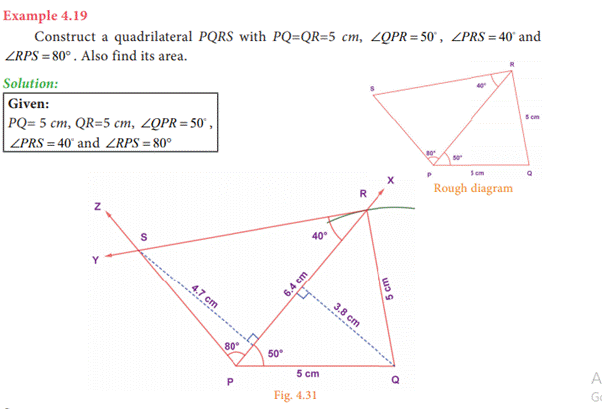
Steps:

1. Draw a line segment PQ = 5 cm.

2. At P on PQ, make ∠ = QPX 50.

3. With Q as center, draw an arc of radius 5 cm. Let it cut PX at R.

4. At R on PR, make ∠ = PRS 40 and at P on PR, make ∠ =° RPS 80. Let them intersect at S.

5. PQRS is the required quadrilateral