Measurements

What is the exact value of π?

π is the constant, it is a non-terminating and non-recurring decimal number. To make the calculations easy, or 3.14 is used as the approximate value of π.

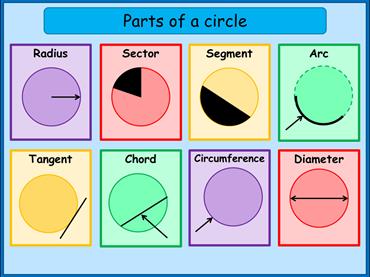
Parts of a Circle:-

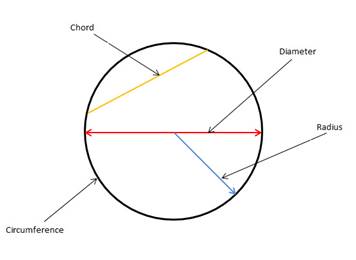
§ A circle is the path traced by a moving point so that its distance from a fixed point is always a constant. The fixed point of the circle is called its ‘center’ and the constant distance is called its ‘radius’.

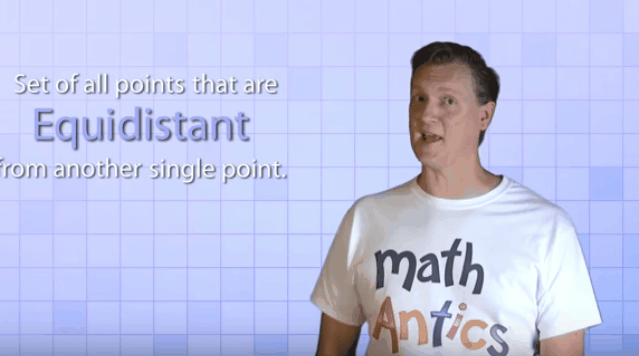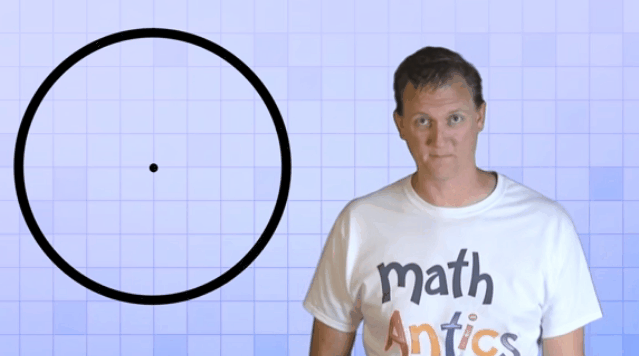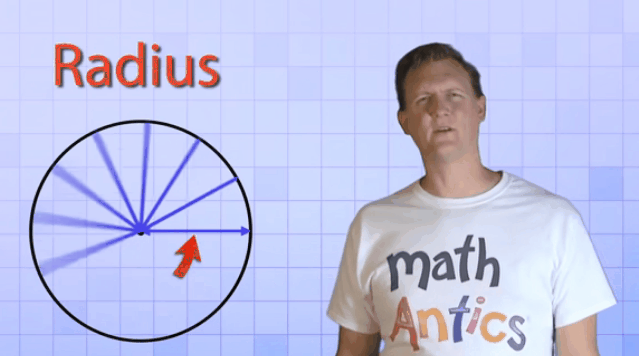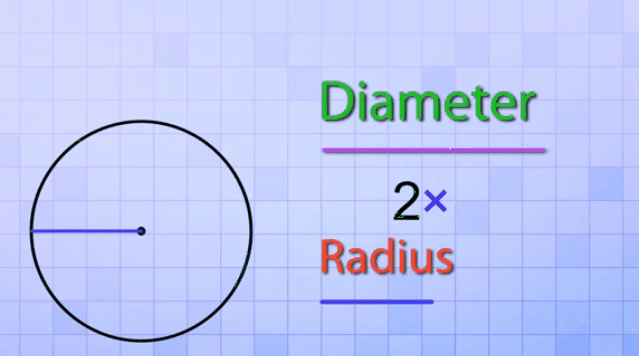
§ If any two points on a circle are joined by a line segment, then the line segment is called a ‘chord’. A chord divides a circle into two parts. A chord which passes through the center of a circle is called as a ‘diameter’. A diameter of a circle divides it into two equal parts. It is also the ‘longest chord’ of a circle.

Circular Arc and Circular Sector:-

A part of the circumference of a circle is called a circular arc. The plane surface that is enclosed between two radii and the circular arc of a circle is called a sector. Each part of a circle which is divided by a chord is called a segment.

The part which has a smaller arc is called as the ‘minor segment’ and the part which has a larger arc is called as the ‘major segment’.

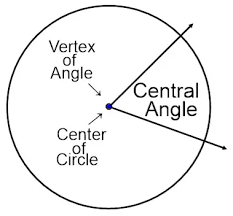
Central Angle:-

The angle formed by a sector of a circle at its center is called the central angle. The vertex of the central angle of the sector is the centre of the circle. Its two arms are the radii.

The central angle of a circle is 360°. If a circle is divided into ‘n’ equal sectors, the central angle of each of the sectors is Ө = .

For example, the central angle of a semicircle = = 180°

Length of the arc and Area of the sector:-

If a circle is divided into 2 equal sectors we will get 2 semi-circles. The length of a semicircular arc is half of the circumference of the circle.

Let the central angle of a sector of radius ‘r’ units as θ°,

§ Ratio of cental angle to 360 is.

§ Length of arc,

§ Area of the sector,

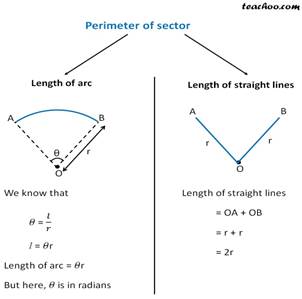
Perimeter of a sector:-

The perimeter of a sector = length of the arc + length of two radii

i.e.

Perimeter of a sector, P = l + 2r units for example:

The perimeter of a semi-circle: P = l+2r units

=

= r(

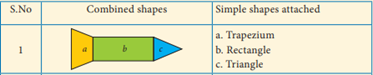
Combined shapes:-

Two or more plane figures joined with the sides of same measure give rise to a new shape called combined shapes.

Perimeter of combined shapes:-

The perimeter of a combined shape is the sum of all the lengths of the sides that form a closed boundary.

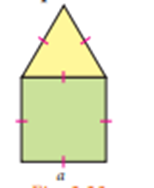
Square of side ‘a’ units and an equilateral triangle of side ‘a’ units combined together. Though a square has 4 sides and an equilateral triangle has 3 sides. So, the perimeter of the combined shape, here is ‘5a’ units.

Area of combined shapes:-

The area of combined shapes is nothing but the sum of all the areas of the simple shapes in it.

Example:

A key-chain is in the form of an equilateral triangle and a semicircle attached to a square of side 5 cm as shown in the below image. Find its area. (π = 3.14, √3 = 1.732)

Solution:

ü A closed plane figure formed by three or more sides is called a ‘polygon’.

ü If all sides and all angles of a polygon are equal, then it is called as a regular polygon.

Examples: equilateral triangle, square etc.,

ü Other polygons are irregular polygons.

Examples: scalene triangle, rectangle etc.,

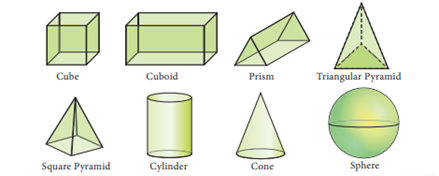
Three dimensional (3-D) shapes:-

The shapes which have three dimensions namely length, breadth and height (depth) are called three dimensional shapes, simply called as 3-D shapes. Some examples of 3-D shapes are:

Faces, Edges and Vertices:-

A cube is made of six, square shaped planes.

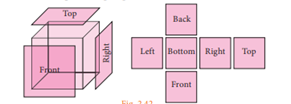
§ These 6, square shaped planes of the cube are known as its faces.

§ The line segment which connects any two faces of a cubes called as Edge

§ Each corner where three edges meet is called as Vertex.

So, a cube has 6 faces, 12 edges and 8 vertices and F+V-E=6+8-12= 2.This is true for any polyhedron and this relation F+V-E =2 is known as Euler’s formula.

The nets for building three dimensional (3-D) shapes:-

The flat shaped card already designed for making the box excluding flaps (dotted lines) is known as net. For example, the following nets build cubes and square pyramids.

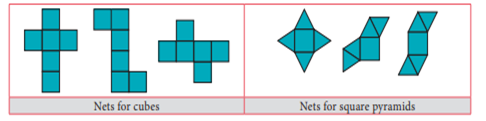
Cross section of solid shapes:-

We can see rectangles and squares in the cross section of a bread loaf and bricks etc.,

For example:-

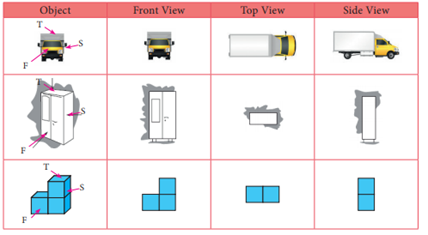
3-D shapes in different views:-

A 3-D object may look different from different positions. Some of the views are front view, top view and side view.