Rational Numbers
1.1 Introduction
➢ We know
about fractions, right? Fractions like
are
obviously clear, that 
represents
1 out of 4 parts, 
is 1 out of 2 parts and so on. But, where are they on the number
line?
➢ As we know,
proper fractions are greater than zero but definitely less than one.
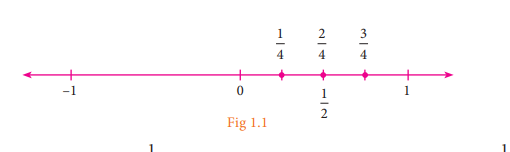
➢As
you see here, 1/ 2 is exactly at the middle of 0 and 1 whereas 1 /4 is exactly
at the middle of 0 and 1/ 2.
Also
3 /4 is exactly at the middle of 1/ 2 and 1.
Also,
when we divide the distance between 0 and 1 roughly into 3 equal parts, the
second part of it, represents 2/3
➢These
fractions 
also
correspond to the decimals 0.25, 0.50, 0.75 and 0.66.
➢The improper
fractions 
etc.,
should be converted into mixed fractions as 
respectively,
so as to locate them easily on the number line as given below.
.
➢It
is clear that 13/5 lies between 2 and 3, 10/3 lies between 3 and 4 whereas 31/7
lies between 4 and 5
Example:
➢If
50 students in a class contribute equally to a total of Rs35 for a cause, how
much does each one contribute? It is
simple. Each one’s contribution is 35/50, simplified to 7/10 of a rupee, which
is 70 paisa (or) Rs 0.70
➢
What if they (50 students) have a debt of Rs35? Shall I denote it by a negative
sign as −7/10?
As
we have seen the extension of whole numbers to integers, these negative
fractions need to be accommodated somewhere on the number line. We know that 0
acts as the mirror to the natural numbers (right of 0) to reflect negative
integers (left of 0). By the same way, we can indicate the negative fractions
on to the left of 0.
Observing the above conversation, one can
see the need of negative fractions coming into the system of numbers that we
have already know about.
1.1.1 Necessity for
extending fractions to rational numbers
➢
For the easy understanding and mathematical clarity, we shall introduce the rational
numbers abstractly by focusing on two properties, namely every number has an
opposite and every non-zero number has a reciprocal.
(i)
Firstly, take the integers and form all possible
‘fractions’ where the numerators are integers and the denominators are non-zero
integers. In this method, a rational number is defined as a ‘ratio’ of
integers. The collection of rational numbers defined in this way will include
the opposites of the fractions.
(ii) Secondly, we could take
all the fractions together with their opposites. This would give us a new
collection of numbers, called the fractions and numbers such as 
,
We know that, the fraction 4/5
satisfies the equation 
since 
and -2
satisfies the equation
,
since −2+2 = 0. However, there is neither a fraction nor an integer that
satisfies the equation 
we have
studied about integers. We you add, subtract or multiply two or more integers,
you will get only an integer. If we divide two integers, we will not always get
an integer.
For example:
are not integers. These situations can be
handled by extending the numbers to another collection of numbers called as rational
numbers.
1.2 Rational numbers
➢Definition
–
The collection of all numbers that
can be written in the form a/b, where a and b are integers and
is called rational numbers which is denoted by
the letter Q. Here, the top number a is called the numerator and the bottom
number b is called the denominator.
Examples:
are
some examples of rational numbers? Also, integers like 7, –4 and 0 are rational
numbers as they can be written in the form
. Mixed
numbers such as
.,are also rational numbers.
So, all integers as well as fractions are rational
numbers. The decimal numbers too, like 0.75, 1.3, 0.888 etc., are also rational
numbers since they can be written in fraction form as
1.2.1 Rational numbers on
a number line
➢
We know how the integers are
represented on a number line. The same way, rational numbers can also be
represented on a number line. Now, let us represent the number −3 /4 on
the number line. Being negative, −3/ 4 would be marked to the left of 0
and it is between 0 and –1. We know that in integers, 1 and –1 are equidistant
from 0 and so are the pairs 2 and –2, 3 and -3 from 0. This remains the same
for rational numbers too. Now, as we mark 3/ 4 to the right of zero, at 3 parts
out of 4 between 0 and 1, the same way, we mark −3 /4 to the left of
zero, at 3 parts out of 4 between 0 and –1 as shown below.
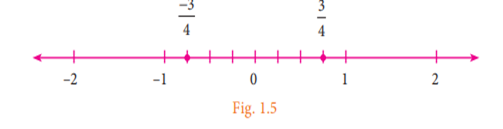
➢ Similarly,
it is easy to say that −5 /2 lies between –2 and -3 as 
Remember
that all proper rational numbers lie between 0 and 1 (or) 0 and –1 just like the
fractions. Now, where do these rational numbers 18/ 5 and − 32/ 7 lie on
a number line? Here, 
and
➢ Now,
18/ 5 lies between 3 and 4 on the number line. The unit part between 3 and 4 is
divided into 5 equal parts and the third part is marked as 3/ 5. Thus, the
arrow mark indicates
. Also, it is clear that the rational number −
32 /7 which is 
lies
between –4 and –5 on the number line. Here, the unit part between −4 and −5
is divided to 7 equal parts and fourth part is marked as 4/ 7. Thus the arrow
mark indicates 
These rational numbers are
shown on the number line as shown below.
Example 1.1
Write
the following decimal numbers as rationals. 
Solution:
(i) 
.
(ii)
(iii)
. ... = (check… you will know how in IX std)
(iv)
.
(v)
1.2.3 Equivalent rational numbers
➢
If the numerator and denominator of a rational
number (say a/b) is multiplied by a non-zero integer (say c), we obtain another
rational number which is equivalent to
the given rational number. This is exactly the same way of getting equivalent
fractions.
➢ For
example, take 
and c =
5 Now,
=
is an equivalent rational number to −4/ 7 and if c is taken as 2,3,-4 etc., the
corresponding rational numbers are 
respectively.
1.2.4 Rational numbers in
standard form
➢ If in a rational number a/ b, the only common
factor of a and b is 1 and b is positive, then the
rational number is said to be in standard form. The rational numbers 4/ 5, -3/7, 1 /6, -4/13.
-50/51 etc., are all said to be in standard form. If a rational number is not
in the standard form, then it can be simplified to get the standard form.
1.2.5 Comparison of rational numbers
➢ You know how to compare integers and fractions
taking two at a time and say which is smaller or greater. Now you will learn
how to compare a pair of rational numbers. z Two
positive rational numbers, say 3/ 5 and 5 /6 can be compared as studied earlier
in comparison of two fractions.
➢ Two negative rational numbers, say −1/ 2
and −4 /5 can be compared as follows.
➢ Find the LCM of the denominators 2 and 5. Mark
these rational numbers on a number line by finding their equivalent rational
numbers having common denominator.
➢ Now,
the equivalent rational numbers having the LCM 10 as common denominator are
found as,
➢ 
and
➢ We know that 
➢ ∴ 
Thus,
➢ If
one of the two rational numbers is negative, say 3 /8 and −2/ 3 , we can easily say that
(or) 
because we know that a positive number is
always greater than a negative number.
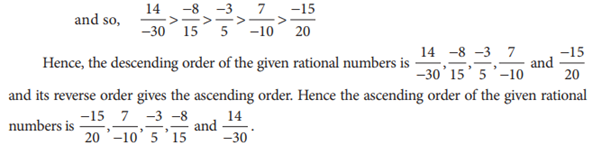
1.2.6 Rational numbers between any two given rational numbers
➢ Think about the situation: Seyyon wanted
to know the number of integers between –10 and 20. He found that there are 9
negative integers, zero and 19 positive integers, a total of 29 integers
between –10 and 20 (excluding –10 and 20). He also finds that there is no other
integer between any two consecutive integers. Is this true for rational numbers
too? Seyyon took two rational numbers −3 /4 and −2 /5. He converted
them to rational numbers having the same denominators (find the LCM of the
denominators).
1.2.7 Alternative method for finding rational numbers between
any two rational numbers by average concept.
➢ In this
method, we shall use the average concept. The average of two numbers a and b is
1/2 (a+b).
➢ Let a and b any two given rational numbers.
➢ By
using the average, we can find many rational numbers between a
and b as c1, c2, c3, c4, c5 etc., as explained in the following.
1.3 Four basic operations
on rational numbers
1.3.1 Addition
(i) Addition of
rational numbers with the same denominators
➢ Add
only the numerators of the two or more rational numbers and write the same
denominator.
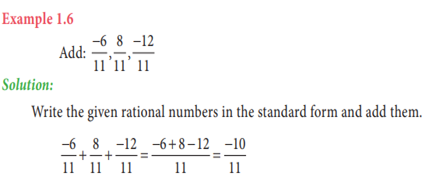
(ii) Addition of
rational numbers with different denominators:
➢ After writing
the given rational numbers in the standard form, take the LCM of the
denominators of the given rational numbers and convert them to equivalent
rational numbers with common denominators (LCM) and then, add the numerators.
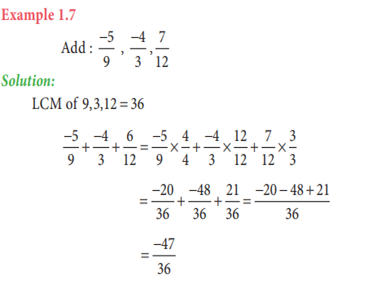
1.3.2 Additive Inverse
What is
?
Now,
Also, 
➢In
the case of integers, we say –5 as the additive inverse of 5 and 5 as the
additive inverse of –5. Here, for rational numbers, −8 /11 is the
additive inverse of 8 /11 and 8/ 11 is the additive inverse of −8/ 11.
1.3.3 Subtraction
➢ Subtracting
two rational numbers, is the same as adding the additive inverse of the second
rational number to the first rational number.
(i)
Subtraction of rational numbers with the same
denominators :
Subtract only the numerators of the two or more
rational numbers and write the same denominator.
(ii) Subtraction of rational numbers with different
denominators:
After writing the given rational
numbers in the standard form, take the LCM of the denominators of the two given
rational numbers and convert them to equivalent rational numbers with common
denominators (LCM) and then, subtract the numerators.
1.3.4 Multiplication
➢
Product of two or more rational numbers can be
found by multiplying the corresponding numerators and denominators of the
numbers and then write them in the standard form.
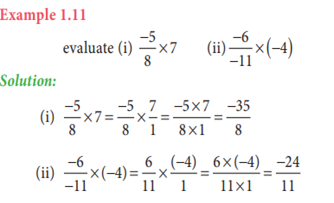
1.3.5 Product of reciprocals and the Multiplicative Inverse
➢ If the product of two rational numbers is 1,
then one rational number is said to be the reciprocal or the multiplicative
inverse of the other.
➢ For the
rational number a, its reciprocal is 
➢ For the
rational number a b , its multiplicative inverse is
1.3.6 Division
➢ We have
seen about the reciprocals of fractions in the earlier classes. The same idea of
reciprocals is extended to rational numbers also. To divide a rational number
by another rational number, we have to multiply the rational number by the
reciprocal of another rational number.
1.5.1 Closure property
➢ The collection of rational numbers (Q) is
closed under addition and multiplication. This means for any two rational
numbers a and b,
are unique rational numbers.
1.5.2 Commutative property
➢ Addition
and multiplication are commutative for rational numbers. That is, for any two
rational numbers a and b ,
(i) 
(ii)
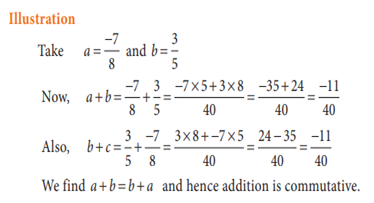
1.5.3 Associative property
➢ Addition and multiplication are associative
for rational numbers. That is, for any three rational numbers a ,b, and c ,
(i)
(ii) 
1.5.4 Additive and Multiplicative Identity property
➢ The identity
for addition is 0 and the identity for multiplication is 1. For any rational
number a there exists unique identity elements 0 and 1 such that
(i)
and
(ii) 
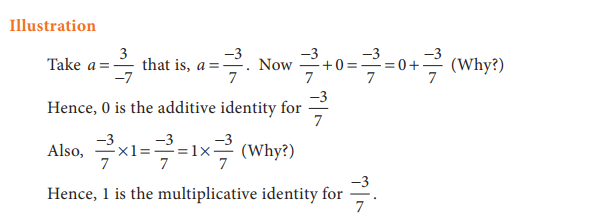
1.5.5 Additive and Multiplicative Inverse property
➢ For any
rational number a there exists a unique rational number –a such that
(Additive Inverse property).
➢ For any
non-zero rational number b there exists a unique rational number 1/ b such that
(Multiplicative Inverse property).
1.5.6 Distributive property
➢ Multiplication
is distributive over addition for the collection of rational numbers. For any
three rational numbers a, b and c,
➢ 
