Algebra

Some Important Definitions:

1.Expression -An algebraic expression is a mathematical phrase having one or more algebraic terms including variables, constants and operating symbols (such as plus and minus signs).

2.Coefficients -The ‘number parts’ of the terms with variables are coefficients.

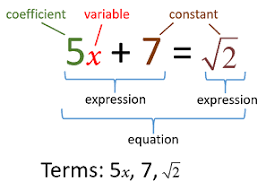
3.Equations -An equation is a statement that asserts the equality of two expressions; the expressions are written one on each side of an “equal to” sign.

For example: 2x + 7 = 17 is an equation (where x is a variable). 2x + 7 forms the Left Hand Side (LHS) of the equation and 17 is its Right Hand Side (RHS).

Linear Equation:

An equation of the form ax + b = 0 where a, b are real numbers such that ‘a’ should not be equal to zero is called a linear equation.

Remember, the highest power of the variable in these expressions is 1.

Examples of some linear equations are 2x, 2x+7, 16 – 7y, etc.

Solving Linear Equations:

There are two methods by which the linear equations can be solved.

(1) Balancing Method

In this method, both the sides of equation are balanced. Let us understand it by an example:

Example: Solve 2x - 10 = 2.

Solution: To balance both the sides, firstly we will add 10 on both the sides of the equation.

2x – 10 + 10 = 2 +10,

On solving, we get

2x = 12

Further, to balance the equation we will divide both the sides by 2

2x / 2 = 12/2

On solving, we get

x = 6.

Thus, x = 6 is the required solution.

Verification: Substitute the value of solution obtained in the original equation. And if after substitution, the LHS becomes equal to RHS then the solution obtained is correct.

As for above example, we obtained x = 6.

Now, let us substitute this value into the original equation 2x – 10 = 2. Then,

LHS = 2(6) – 10 = 12 – 10 = 2

RHS = 2

Here, it is observed that LHS = RHS, thus the solution obtained is correct.

(2) Transposing Method:

In this method, constants or variables are transposed from one side of the equation to other until the solution is obtained. Let us understand it by an example:

Example: Solve 2x – 5 = 5

Solution: Firstly, we will transpose the integer -5 from LHS to RHS, thus we will get

2x = 5 + 5

On solving, we get

2x = 10

Now, we will transpose the 2 from LHS to RHS, thus we will get

x = 10 / 2

On solving, we get

x = 5.

Thus, x = 5 is the required solution.

Verification: Again, we will the substitute the obtained solution into the original equation.

Thus, LHS = 2 (5) – 5 = 10 - 5 = 5

RHS = 5

Since, it is observed that LHS = RHS, the solution obtained is correct.

Example 1: Solve a + 5 = 15.

Solution:

Transposing 5 to RHS, thus we will get

a = 15 – 5

a = 10

Example 2: Solve x/ 2 + 2 = 9/4.

Solution:

Let us transpose 2 on RHS, thus we will get

x/2 = 9/4 – 2

x/2 = 1/4

Now, transposing ½ on RHS, we get

x = 2/4 i.e. x = 1/2

Applications of linear equations:

Usually, one will encounter many practical situations where he needs to apply the methods to solve the linear equations. Let us consider an example to understand it.

Example 1: Sum of two numbers is 70. One of the numbers is 10 more than the other number. What are the numbers?

Solution: Let us assume the two numbers to be x and y.

Now, it’s given that sum of these two numbers is 70, thus, we can write

x + y = 70

Further, it is given that one of the numbers is 10 more than the other. So, let y be 10 more than x, thus, we can write

y = x +10

Substituting value of y, we get,

x + x + 10 = 70

2x + 10 = 70

Transposing 10 on RHS,

2x = 70 – 10

2x = 60

Transposing 2 on RHS,

2x = 60

x = 30.

Now, the other number y will be x + 10 = 30 + 10 = 40 i.e. y = 40

Hence, the two desired numbers are 30 and 40.

Example 2: The sum of three consecutive multiples is 60. What are these integers?

Solution:

Let the three consecutive integers be a, a+1 and a+2.

Given, a + a + 1 + a + 2 = 60

3a + 3 = 60

Transposing 3 on LHS, we get,

3a = 60 – 3

3a = 57

On solving, a = 57/3, we get

a = 19

a + 1 = 20 and a + 2 = 21

Thus, the three consecutive integers are 19, 20 and 21.

Example 3: The organisers of an essay competition decide that a winner in the competition gets a prize of Rs 100 and a participant who does not win gets a prize of Rs 25. The total prize money distributed is Rs 3,000. Find the number of winners, if the total number of participants is 63.

Solution:

Let the number of winners be z. Thus, the number of participants not winning will be 63 – z.

Given, amount of winners is (100 x z) Rs i.e. 100z Rs.

Amount given to participants not winning = 25 x (63 – z) Rs = (1575 – 25z) Rs.

Given, 100z + 1575 – 25z = 3000

Now, transposing 1575 on RHS, we get

100z – 25z = 3000 – 1575

75z = 1425

Now, dividing both the sides by 75, we get

75z / 75 = 1425 / 75

z = 19

Hence, the numbers of winners are 19.

Example 4: Rahul’s age is three times his son’s age. Ten years ago he was five times his son’s age. Find their present ages.

Solution: Let the age of Rahul’s son be x. Hence, his age will be 3x.

Given, 10 years ago Rahul’s age was five times his son’s age. So, we can write

(3x – 10) = 5 (x – 10)

3x – 10 = 5x – 50

Transposing 5x to LHS and 10 to RHS, we get

3x – 5x = -50 + 10

-2x = -40

Dividing both the sides by 2, we get

So, x = 20

3x = 60.

Thus, present age of Rahul is 60 and his son’s age is 20.

Graphs:

Graph is just a visual method for showing relationships between numbers.

A graph looks like-

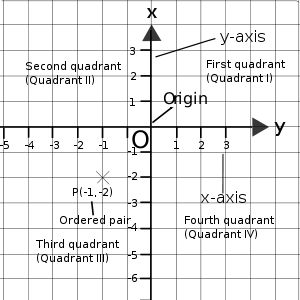
Cartesian System:

Rene Descartes system of fixing a point with the help of two measurements, horizontal and vertical, is known as Cartesian system, in his honour. The horizontal line is named as XOX', called the X-axis. The vertical line is named as YOY', called the Y- axis. Both the axes are called coordinate axes. The plane containing the X axis and the Y axis is known as the coordinate plane or the Cartesian plane.

Ordered Pairs: A point is named by its ordered pair of the form of (x, y). The first number corresponds to the x-coordinate and the second to the y-coordinate. To graph a point, you draw a dot at the coordinates that corresponds to the ordered pair. It's always a good idea to start at the origin.

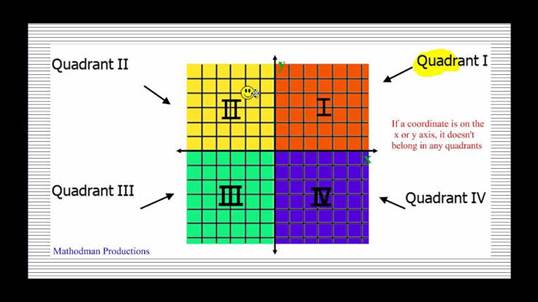
Quadrants: The graph is divided into four quadrants, or sections, based on those values.

· The first quadrant is the upper right-hand corner of the graph, the section where both x and y are positive.

· The second quadrant, in the upper left-hand corner, includes negative values of x and positive values of y.

· The third quadrant, the lower left-hand corner, includes negative values of both x and y.

· Finally, the fourth quadrant, the lower right-hand corner, includes positive values of x and negative values of y.

Linear Graph

Linear means straight and a graph is a diagram which shows a connection or relation between two or more quantity. So, the linear graph is nothing but a straight line or straight graph which is drawn on a plane connecting to points on x and y coordinates. We use linear relations in our everyday life and by graphing those relations in a plane, we get a straight line.

Linear equations use one (or more) variables where one variable is dependent on the other(s).

The independent variable (traditionally plotted on the x axis) is what can freely change. The dependent variable (traditionally plotted on the y axis) is what is affected by the independent variable.

For Example:

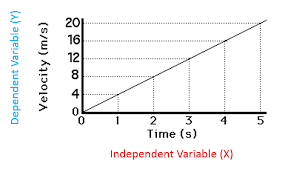
Linear Equations in Two Variables

Equations of degree one and having two variables are known as linear equations in two variables. It is of the form, ax +by +c = 0, where a, b and c are real numbers, and both a and b not equal to zero.

Equations of the form ax+by = 0; where a and b are real numbers, and a,b ≠ 0, is also linear equations in two variable.

Solution of a Linear Equation in Two Variables

The solution of a linear equation in two variables is a pair of numbers, one for x and one for y which satisfies the equation. There are infinitely many solutions for a linear equation in two variables.

For example,  x+2y =6 is a linear equation and some of its solution are (0,3),(6,0),(2,2) because, they satisfy  x+2y=6.

Q1.   Draw the graph of each of the following linear equations in two variables:

(i) x + y = 4            ii) x – y = 2            (iii) y = 3x            (iv) 3 = 2x + y

Sol: (i) x + y = 4       ⇒                      y = 4 – x

           If we have                              x = 0, then y = 4 – 0 = 4

                                                        x = 1, then y = 4 – 1 = 3

                                                        x = 2, then y = 4 – 2 = 2

∴ We get the following table:

           Plot the ordered pairs (0, 4), (1, 3) and (2, 2) on the graph paper. Joining these points, we get a line AB as shown below.

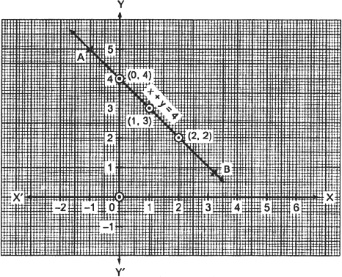
Thus, the line AB is the required graph of x + y = 4.

(ii) x – y = 2

⇒ y = x – 2

      If we have                        x = 0,then y = 0 – 2 = –2

                                              x = 1,then y = 1 – 2 = –1

                                              x = 2, then y = 2 – 2 = 0

∴ We have the following table:

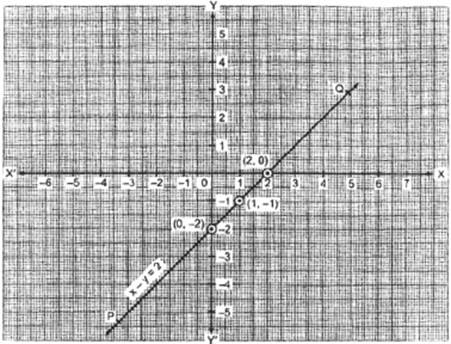
Plot the ordered pairs (0, –2), (1, –1) and (2, 0) on the graph paper. Joining these points, we get a straight line PQ as shown below:

Thus, the line PQ is required graph of x – y = 2.

(iii) y = 3x

      If                  x = 0, then y = 3(0) ⇒ y = 0

                           x = 1, then y = 3(1) ⇒ y = 3

                           x = –1, then y = 3(–1) ⇒ y = –3

∴ We get the following table

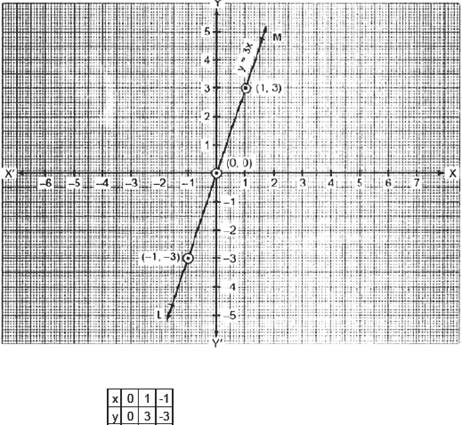
Plot the ordered pairs (0, 0), (1, 3) and (–1, –3) on the graph paper. Joining these points, we get the straight line LM.

Thus, LM is the required graph of y = 3x.

Note: The graph of the equation of the form y – kx is a straight line which always passes through the origin.

(iv) 3 = 2x + y ⇒ y – 3 – 2x

∴                        If x = 0, then y = 3 – 2(0) ⇒ y = 3

                                If x = 1, then y = 3 – 2(1) ⇒ y = 1

                                If x = 2, then y = 3 – 2(2) ⇒ y = –1

Plot the ordered pairs (0, 3), (1, 1) and (2, 1) on the graph paper. Joining these points, we get a line CD.

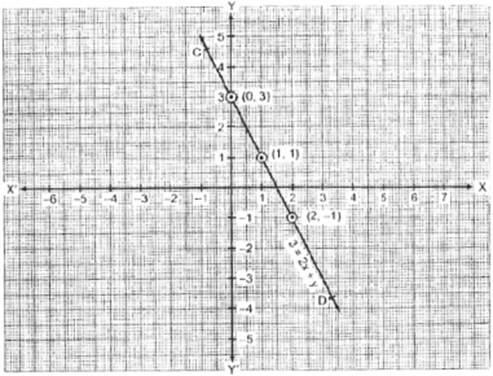
Thus, the line CD is the required graph of 3 –2x–ry.