Geometry

1 Introduction

In the first term, we have learnt about similar and congruent triangles and the construction of quadrilaterals. Now, we will learn about the Pythagorean theorem and the construction of trapeziums and parallelograms.

2 The Pythagorean Theorem

The Pythagorean theorem or simply Pythagoras theorem, named after the ancient Greek Mathematician Pythagoras (570-495 BC (BCE)) is definitely one of the most famous and celebrated theorems in the whole of mathematics. People have proved this theorem in numerous ways possibly the most for any mathematical theorem. They are very diverse which include both geometric and algebraic proofs dating back to thousands of years.

Statement of the theorem

In a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.

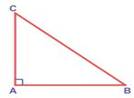
In ∆ ABC, BC² = AB² + AC²

Visual Illustration:

The given figure contains a triangle of sides of measures 3 units, 4 units and 5 units. From this well known 345 − − triangle, one can easily visualise and understand the meaning of the Pythagorean theorem.

In the figure, the sides of measure 3 units and 4 units are called the legs or sides of the right angled triangle. The side of measure 5 units is called the hypotenuse. Recall that the hypotenuse is the greatest side in a right angled triangle

Now, it is easily seen that a square formed with side 5 units (hypotenuse) has 5 × 5 = 25 unit squares (small squares) and the squares formed with side 3 units and 4 units have 3 3 × = 9 unit squares and 4 × 4 = 16 unit squares respectively. As per the statement of the theorem, the number of unit squares on the hypotenuse is exactly the sum of the unit squares on the other two legs (sides) of the right angled triangle. Isn’t this amazing?

Yes, we find that

5×5 = 3×3+4×4

i.e. 25 = 9+16 (True)

Proof of the theorem using similarity of triangles

Given: ∠BAC= 90⁰

To prove: BC² = AB² + AC²

Construction: Draw AD ⊥ BC

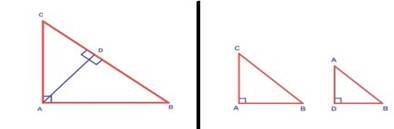
Proof:

In ∆ ABC and ∆ DBA,

∠B is common and ∠BAC = ∠ADB = 90⁰

Therefore, ∆ABC ~ ∆DBA (AA similarity)

Hence, the ratio of corresponding sides are equal.

Þ

Þ AB² = BC × DB ------------(1)

Similarly ∆ABC ~ ∆DBA,

Þ

Þ AC² = BC × DC --------------(2)

Adding (1) and (2), we get

AB² + AC² = BC × DB + BC × DC

= BC × (DB + DC)

= BC × BC

∴ ⇒ AB2 + AC² = BC² and

Hence the proof of the theorem.

3 Converse of Pythagoras theorem

If in a triangle, the square on the greatest side is equal to the sum of squares on the other two sides, then the triangle is right angled triangle.

Example:

In the triangle ABC,

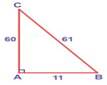
AB² + AC² = 11² +60² = 3721 = 61²= BC²

Hence, ∆ ABC is a right angled triangle.

We shall now see a few examples on the use of Pythagoras theorem in problems.

Example: 1

In the figure, AB ⊥ AC

a) What type of ∆ is ABC?

b) What are AB and AC of the ∆ ABC?

c) What is CB called as?

d) If AC = AB then, what is the measure of ∠B and ∠C?

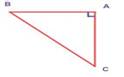
Solution

a) ∆ ABC is right angled as AB ⊥ AC at A.

b) AB and AC are legs of ∆ ABC.

c) CB is called as the hypotenuse.

d) ∠B + ∠C = 90⁰ and equal angles are opposite to equal sides. Hence, ∠B = ∠C = 90⁰/2 = 45⁰

Example: 2

Can a right triangle have sides that measure 5cm, 12cm and 13cm?

Solution:

Take a = 5, b = 12 and c = 13

Now, a² + b² = 5² + 12² = 25 + 144 = 169 = 13² = c²

By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.

Example: 3

A 20-feet ladder leans against a wall at height of 16 feet from the ground. How far is the base of the ladder from the wall?

Solution:

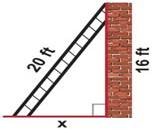
The ladder, wall and the ground form a right triangle with the ladder as the hypotenuse. From the figure, by Pythagoras theorem,

Þ 20² = 16² + x²

Þ 400 = 256 + x²

Þ x² = 400 – 256 = 144 = 12²

Þ x = 12 feet

Þ Therefore, the base (foot) of the ladder is 12 feet away from the wall.

4 The Altitude –on –Hypotenuse theorem (without proof)

Here, the hypotenuse of a right angle triangle is taken as its base. Draw an altitude to it (as given in the figure). We will have two more, smaller right triangles. Now, all these three triangles are similar!

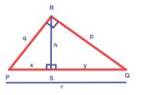
Theorem:

If an altitude is drawn to the hypotenuse of an right angled triangle, then

(i) The two triangles are similar to the given triangle and also to each other.

That is, ∆PRQ ~ ∆PSR ~ ∆RSQ

(ii) h² = xy

(iii) p² = yr and q² =xr , where r = x + y

Example:

∆ ABC is equilateral and CD of the right triangle BCD is 8cm. Find the side of the equilateral ∆ ABC and also BD.

Solution:

As ∆ ABC is equilateral from the figure, AB = BC = AC = (x−2) cm.

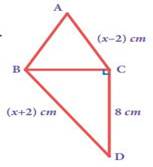
∴ From ∆ BCD, by Pythagoras theorem

BD² = BC² + CD²

(x+2)² = (x-2)² + 8²

X² + 4 + 4x = x² + 4 – 4x + 8²

Þ 8x = 8²

Þ X = 8

Þ ∴ The side of the equilateral ∆ ABC = 6 cm and BD =10cm.

Example:

From the figure, find x and y and verify ∆ ABC is a right angled triangle.

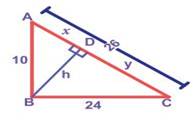
Solution:

Now, by altitude-on-hypotenuse theorem,

Þ AB² = AD × AC gives

Þ 10² = X × 26

Þ X = 100/26 = 50/13 units

BC² = CD × AC, gives

Þ 24² = y × 26

Þ Y = 576/26 = 288/13 units

In∆ ABC, AB² + BC² = 10² + 24² = 100+576 = 676 = 26² = AC²

Therefore, ∆ ABC is a right angled triangle.

5 Construction of Trapeziums

In the first term, we have learnt how to construct the quadrilaterals. To draw a quadrilateral, how many measurements do you need? 5 measurements. Isn’t it?

Let us see the special quadrilaterals which need less than 5 measurements. Based on the nature of sides and angles of a quadrilateral, it gets special names like trapezium, parallelogram, rhombus, rectangle, square and kite.

Now, you will learn how to construct trapeziums.

Trapezium is a quadrilateral in which a pair of opposite sides are parallel.

To construct a trapezium, draw one of the parallel sides as a base and on that base construct a triangle with the 2 more measurements.

Now, through the vertex of that triangle, construct the parallel line opposite to the base so that the triangle lies between the parallel sides.

As the fourth vertex lies on this parallel line, mark it with the remaining measure. Hence, we need four independent measures to construct a trapezium. The given shapes are examples of trapeziums.

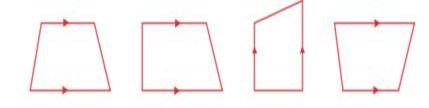
Note: The arrow marks in the above shapes represent parallel sides.

If the non-parallel sides of a trapezium are equal in length and form equal angles at one of its bases, then it is called an isosceles trapezium.

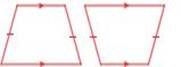
5.1 Constructing a trapezium when its three sides and one diagonal are given:

Example:

Construct a trapezium BOAT in which is parallel to , BO=7cm, OA=6cm, BA=10cm and TA=6cm. Also find its area.

Solution:

Given:

BO=7cm, OA=6cm, BA=10cm, TA=6cm and ||

Steps:

1. Draw a line segment BO = 7cm.

2. With B and O as centres, draw arcs of radii 10cm and 6cm respectively and let them cut at A.

3. Join BA and OA.

4. Draw AX parallel to BO

5. With A as centre, draw an arc of radius 6cm cutting AX at T.

6. Join BT. BOAT is the required trapezium.

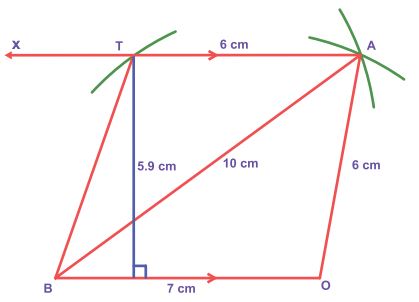
Area of the trapezium BOAT =

5.2 Constructing a trapezium when its three sides and one angle are given:

Example:

Construct a trapezium CARD in which CA is parallel to DR, CA=9cm, ∠CAR = 70⁰ , AR=6cm and CD=7cm. Also find its area.

Solution:

Given:

CA=9cm, ∠CAR= 70° AR=6cm, and CD=7cm and CA || DR

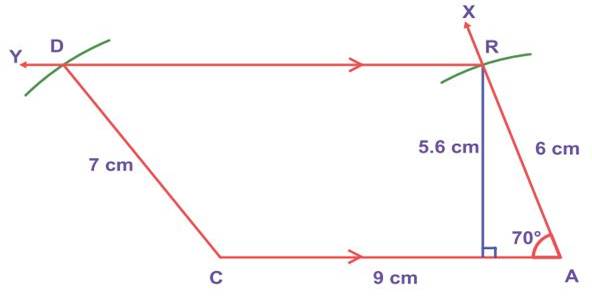
Steps:

1. Draw a line segment CA= 9cm.

2. Construct an angle ∠CAX = 70° at A.

3. With A as centre, draw an arc of radius 6cm cutting AX at R.

4. Draw RY parallel to CA.

5. With C as centre, draw an arc of radius 7cm cutting RY at D.

6. Join CD. CARD is the required trapezium.

Calculation of area:

Area of the trapezium CARD =

5.3 Constructing a trapezium when its two sides and two angles are given:

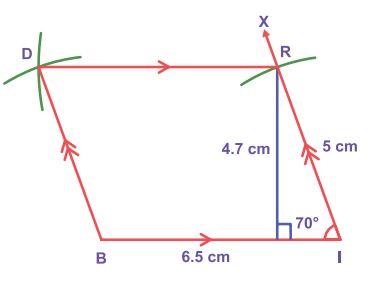
Example:

Construct a trapezium DEAN in which DE is parallel to NA, DE=7cm, EA=6.5cm ∠EDN = 100° and ∠DEA = 70° . Also find its area.

Solution:

Given:

DE=7cm, EA=6.5cm ∠EDN = 100° and ∠DEA = 70° and DE || NA

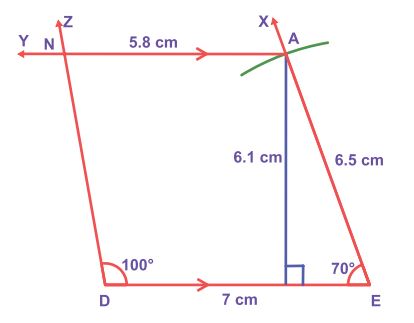
Steps:

1. Draw a line segment DE= 7cm.

2. Construct an angle ∠DEX = 70° at E.

3. With E as centre draw an arc of radius 6.5cm cutting EX at A.

4. Draw AY parallel to DE.

5. Construct an angle ∠EDZ = 100° at D cutting AY at N.

6. DEAN is the required trapezium.

Calculation of area:

Area of the trapezium CARD =

5.4 Constructing a trapezium when its four sides are given:

Example:

Construct a trapezium DESK in which DE is parallel to KS, DE=8cm, ES=5.5cm, KS =5cm and KD=6cm. Find also its area.

Solution:

Given:

DE=8cm, ES=5.5cm, KS =5cm, KD=6cm and DE || KS

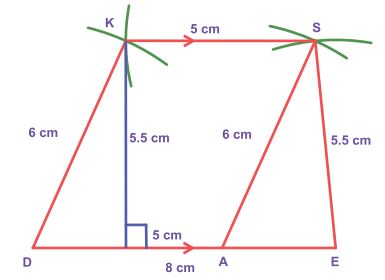
Steps:

1. Draw a line segment DE= 8cm.

2. Mark the point A on DE such that DA=5cm.

3. With A and E as centres, draw arcs of radii 6cm and 5.5cm respectively. Let them cut at S. Join AS and ES.

4. With D and S as centres, draw arcs of radii 6cm and 5cm respectively. Let them cut at K. Join DK and KS.

5. DESK is the required trapezium.

Calculation of area:

Area of the trapezium CARD =

6 Construction of Parallelograms

In the previous session, we have learnt how to construct trapeziums. In a trapezium, a pair of opposite sides are parallel, Isn’t it? What about the other pair? They are non-parallel sides.

Can you guess the quadrilaterals which have both pairs of opposite sides as parallel? Yes, you call them as parallelogram, rhombus, rectangle and square.

Here, we will come to know about parallelograms. A parallelogram is a quadrilateral in which the opposite sides are parallel.

To construct a parallelogram, draw a triangle with the given measurements.

Then, the fourth vertex is found by using the measurements as same as the adjacent sides.

Hence, three independent measurements are enough to construct a parallelogram.

6.1 Constructing a parallelogram when its two adjacent sides and one angle are given:

Example:

Construct a parallelogram BIRD with BI=6.5cm, IR=5cm and ∠BIR = 70° . Also find its area.

Solution:

Given:

BI=6.5cm, IR=5cm and ∠BIR = 70°

Steps:

1. Draw a line segment BI=6.5cm.

2. Make an angle ∠ = BIX 70° at I on BI.

3. With I as centre, draw an arc of radius 5cm cutting IX at R.

4. With B and R as centres, draw arcs of radii 5cm and 6.5cm respectively. Let them cut at D.

5. Join BD and RD. 6. BIRD is the required parallelogram.

Calculation of area:

Area of the parallelogram BIRD = bh sq. Units

= 6.5 × 4.7 = 30.55 sq. cm

6.2 Constructing a parallelogram when its two adjacent sides and one diagonal are given:

Example:

Construct a parallelogram CALF with CA=7cm, CF=6cm and AF=10cm. Also find its area.

Solution:

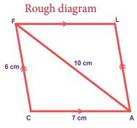
Given:

CA=7cm, CF=6cm and AF=10cm

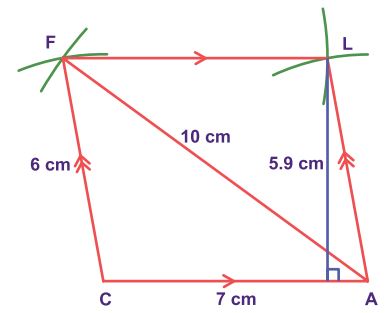
Steps:

1. Draw a line segment CA=7cm.

2. With C and A as centres, draw arcs of radii 7cm and 6cm respectively. Let them cut at F.

3. Join CF and AF.

4. With A and F as centres, draw arcs of radii 6cm and 7cm respectively. Let them cut at L.

5. Join AL and FL. 6. CALF is the required parallelogram.

Calculation of area:

Area of the parallelogram CALF = bh sq.units

= 7 ×5.9 = 41.3 sq.cm

6.3 Constructing a parallelogram when its two diagonals and one included angle are given:

Example:

Construct a parallelogram DUCK with DC=8cm, UK=6cm and ∠DOU = 110° . Also find its area.

Solution:

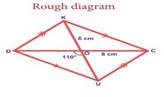
Given:

DC=8cm, UK=6cm and ∠DOU = 110°

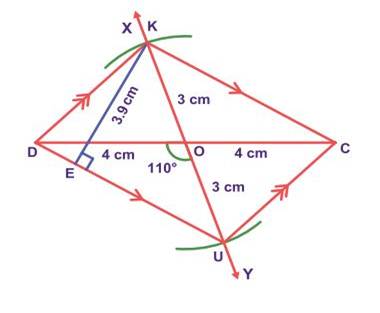
Steps:

1. Draw a line segment DC=8cm.

2. Mark O the midpoint of DC.

3. Draw a line XY through O which makes ∠DOY = 110°.

4. With O as centre and 3cm as radius draw two arcs on XY on either sides of DC. Let the arcs cut OX at K and OY at U

5. Join DU, UC, CK and KD.

6. DUCK is the required parallelogram.

Calculation of area:

Area of the parallelogram DUCK = bh sq. Units

= 5.8 × 3.9 = 22.62sq cm